Расчет элементов конструкции на прочность и жесткость при кручении
Задача
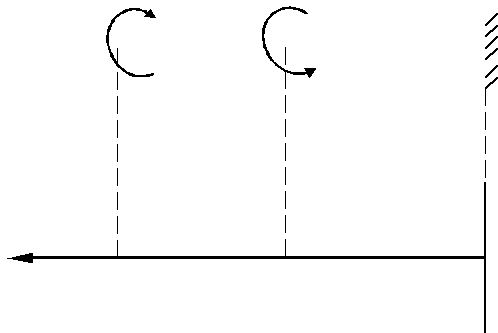
Определите диаметр стального бруса на каждом из его участков по условиям прочности и жесткости. Для материала бруса принять [ t ]= 30 МПа;
| [ j 0 ]= 0,02 | рад / м ; G =8 ×104 | МПа . М 1=0,9 кНм ; | М 2=1,4 кНм . | ||||||||||||||||||||||
| Решение | М 1 | М 2 | |||||||||||||||||||||||
| 1. Разбиваем брус на участки. | I | II | |||||||||||||||||||||||
| 2. | Определяем | ординатыэпюр | 0,9 | ||||||||||||||||||||||
| крутящих моментов М к на участках бруса, | |||||||||||||||||||||||||
| пользуясь методом сечений. | 0,5 | ||||||||||||||||||||||||
| МкI | = M 1=0,9 | кНм | |||||||||||||||||||||||
| МкII | = M 1- M 2 | = (0,9 -1,4) ×103 = -0,5 кНм | Мк кНм | ||||||||||||||||||||||
3. Строим эпюру крутящих моментов.
4. Определяем диаметры бруса для участка I по условиям прочности и жёсткости.
а) по условию прочности:
| М кI | 0,9 ×103 | |||||||||||||||||||||||||||||
| d I ³ 3 | ³ 3 | ³ | 3 | 0,15 | ×10 | -3 | ³ | 0,53×10 | -1 | м ³53 мм; | ||||||||||||||||||||
| 0,2[ t | ] | 0,2 ×30 ×106 | ||||||||||||||||||||||||||||
| б) по условию жесткости: | ||||||||||||||||||||||||||||||
| 0,9 ×103 | ||||||||||||||||||||||||||||||
| М | ||||||||||||||||||||||||||||||
| d I ³ 4 | кI | ³ 4 | ³ 4 | 0,06 ×10-4 | ³ 0,49 ×10-1 м ³ 49 мм | |||||||||||||||||||||||||
| 0,1 G [ j 0 | ] | |||||||||||||||||||||||||||||
| 0,1×8 ×10 | 4 ×106 ×0,02 | |||||||||||||||||||||||||||||
| Принимаем | величину диаметра | бруса равной d I = 54 мм (ближайшее | ||||||||||||||||||||||||||||
большее четное значение).
4. Определяем диаметры бруса для участка II по условиям прочности и жёсткости.
а) по условию прочности:
| М | 0,5 ×103 | |||||||||||||||||||||
| d II ³ 3 | кII | ³ 3 | ³ 3 0,08 ×10-3 | ³ 0,43×10-1 | м ³43 мм; | |||||||||||||||||
| 0,2[ t ] | 0,2 ×30 ×106 | |||||||||||||||||||||
| б) по условию жесткости: | ||||||||||||||||||||||
| 0,5×103 | ||||||||||||||||||||||
| М | кII | |||||||||||||||||||||
| d II ³ 4 | ³ 4 | ³ 4 0,03×10-4 | ³ 0,42 ×10-1 м ³ 42 мм | |||||||||||||||||||
| 0,1 G [ j 0 ] | ||||||||||||||||||||||
| 0,1 | ×8 ×104 ×106 ×0,02 | |||||||||||||||||||||
| Принимаем величину диаметра бруса равной d II = 44 мм. | ||||||||||||||||||||||
| Ответ: d I = 54 мм; | d II =44 мм. |
Решите задачу в соответствии со своим вариантом
| Вариант | М1, кНм | М2, кНм | М3, кНм |
| 1, 11, 21 | 0,9 | 1,5 | 1,5 |
| 2, 12, 22 | 2,5 | 1,3 | 0,8 |
| 3, 13, 23 | 1,1 | 0,7 | 3,2 |
| 4, 14, 24 | 0,8 | 1,4 | 0,7 |
| 5, 15, 25 | 4,2 | 2,0 | 1,2 |
| 6, 16 | 1,3 | 1,3 | 0,7 |
| 7, 17 | 4,5 | 1,4 | 0,9 |
| 8, 18 | 1,2 | 0,9 | 4,0 |
| 9, 19 | 1,9 | 2,0 | 0,6 |
| 10, 20 | 3,0 | 1,0 | 1,9 |
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||











М 1 М 2 М 3

М 1 М 2 М 3
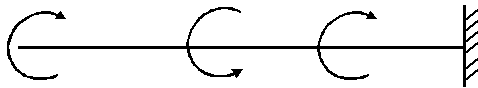
М 1 М 2 М 3

М 1 М 2 М 3
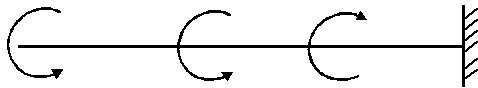
Определение размеров сечения бруса
Задача
Для заданного бруса постройте эпюру крутящих моментов и подберите размеры сечения в двух вариантах: а) круг; б) кольцо с отношением
| внутреннего и наружного диаметров | d 0 | = 0,8, приняв | [ t ]= 100 МПа, моменты | ||
| d | |||||
| М 1=400 Нм, | М 2=200 Нм, М 3=600 Нм. Сравнить | затраты материалов, | |||
затрачиваемых на изготовление бруса, по обоим расчетным вариантам.
Решение
1. Разбиваем брус на участки.
2. Определяем ординаты эпюр крутящих моментов М к на участках бруса,
| пользуясь методом сечений. | М 1 | М 2 | М 3 | |||||||||||||||||||||||
| МкI | = M 1=400 Нм | |||||||||||||||||||||||||
| МкII | = M 1- M 2 | = 400 - 200 = 200 Нм | ||||||||||||||||||||||||
| I | II | II | ||||||||||||||||||||||||
| Мк III | = M 1- M 2 | - M 3=400-200-600= -400 Нм | ||||||||||||||||||||||||
| 3. Строим эпюру крутящих моментов. | ||||||||||||||||||||||||||
| М к кНм | ||||||||||||||||||||||||||
| 4. По эпюре крутящих моментов | ||||||||||||||||||||||||||
| определяем опасные сечения на участках I и III | ||||||||||||||||||||||||||
| Мк max=400 Нм. |
5. Находим необходимый полярный момент сопротивления из условия прочности при кручении.
t max= M к max£[ t ]
Wp
Wp = M [ tк max]=400×6=4×10-6 м 3=4×103 мм 3.100 10
6. Определяем диаметр бруса круглого сечения.
pd 3
W = кр
| d кр = | 3 | 16 Wp | = | 3 | 16 × 4000 | = 26,43 мм | |||
| p | 3,14 | ||||||||
Принимаем величину диаметра круглого бруса равной dкр = 28 мм.
7. Определяем диаметры бруса кольцевого сечения.
| pdкр 3 | d | |||||||||||
| Wp = | (1 - с | ); с = | = 0,8 | |||||||||
| d | ||||||||||||
| Наружный диаметр кольца | ||||||||||||
| 16 Wp | ||||||||||||
| d = 3 | = | 3 | 16 × 4000 | = 31,47 мм | ||||||||
| p (1 - c 4) | 3,14(1 - 0,84) |

Принимаем величину наружного диаметра кольца равной d = 32 мм. Внутренний диаметр кольца
d 0=0,8 d =0,8×32=25,6 мм
Принимаем величину внутреннего диаметра кольца равной d 0 = 26 мм.
9. Сравниваем массы брусьев круглого и кольцевого сечения.
Так как брусья круглого и кольцевого сечения имеют одинаковую длину
и изготовлены из одного и того же материала, то массы брусьев будут относиться, как площади.
Площадь бруса круглого сечения
| А = | pdкр | = | 3,14 × 282 | = 615 мм 2. | |||||||||||||
| кр | |||||||||||||||||
| Площадь бруса кольцевого сечения | |||||||||||||||||
| А = | p | (d 2 - d 0 2) = | 3,14 | (322 - 262) = 273 мм 2. | |||||||||||||
| к | |||||||||||||||||
| Сравниваем массы брусьев | |||||||||||||||||
| mкр | = | Aкр | = | = 2,25 | |||||||||||||
| m | А | ||||||||||||||||
| Ответ: dкр | = 28 мм; | d =32 мм; d 0=26 мм;брус круглого сечения тяжелее |
бруса кольцевого сечения в 2,25 раза, во столько же раз, то есть в 2,25 раза затраты материала на брус круглого сечения будут больше.
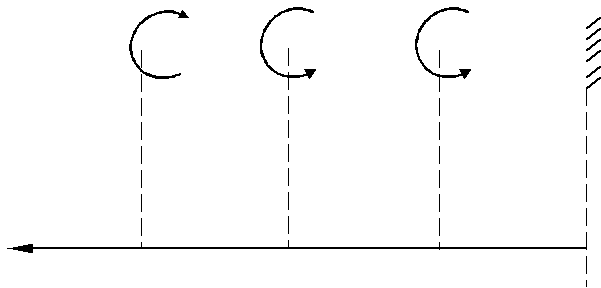
Решите задачу в соответствии со своим вариантом
| Вариант | М1, Нм | М2, Нм | М3, Нм |
| 1, 11, 21 | |||
| 2, 12, 22 | |||
| 3, 13, 23 | |||
| 4, 14, 24 | |||
| 5, 15, 25 | |||
| 6, 16 | |||
| 7, 17 | |||
| 8, 18 | |||
| 9, 19 | |||
| 10, 20 |
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||
| М 3 | М 2 | М 1 | ||||












М 1 М 2 М 3
М 1 М 2 М 3
М 1 М 2 М 3

 М 1 М 2 М 3
М 1 М 2 М 3
