Пример. Автомобиль – вездеход массой m =4000 кг, имея в точке А начальную скорость 𝑣0=2 м/с, преодолевает препятствие ABCD в пересеченной местности, профиль которого характеризуется уклонами α1=15°, α2=10°, α3=5° (рисунок 1.1). Длина участка АВ составляет 20м, время движения по участку ВС t 2=10с. Силы тяги по участкам составляют F 1 =12кН, F 2 = 0, F 3 = 0, силы сопротивления движению R 1=4 кН, R 2=4,8 кН, R 3=6 кН. Определить скорости автомобиля в точках В и С, время движения t 3по участку CD до остановки в точке D и его длину 𝑙3. Считая, что в точках перелома профиля В и С ударов не происходит, а скорость плавно изменяет свое направление, сохраняя модуль, автомобиль за время преодолевания препятствия ABCD не отрывается от поверхности последнего.
Рисунок 1.1 – Профиль препятствия
Решение
Рассмотрим движение автомобиля по участку АВ (рисунок 1.2).
На автомобиль действуют следующие внешние силы: сила тяжести 
, нормальная реакция грунта 
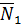, сила внешнего сопротивления (сопротивление воздуха, сопротивление движению вследствие образования колеи и др.причин) 
1, сила тяги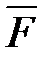 
1 , являющаяся движущей силой.
Составим дифференциальное уравнение движения центра масс автомобиля в проекции на ось X:
| (1.2) |
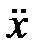= ∑ Fkx,
где m – масса автомобиля; x – координата его центра масс; Fkx - проекции внешних сил на ось x, действующих на автомобиль.
Оно в развернутом виде:
m 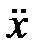= F1 – R1 – G sinα1.
Откуда
| (1.3) |
= 
= 
- 
= 
- 
.
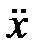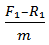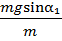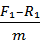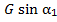Рисунок 1.2 – Расчетная схема для участка АВ
По исходным данным задачи на участке АВ:
| (1.4) |
= 
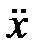- 9,81∙0,259 = 0,21 м/с2.
| (1.5) |
| (1.6) |
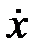= 0,21 t + c1,
x= 0,105 t 2+ c 1 t + c 2 .
По начальным условиям движения на участке АВ при t= 0: 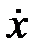0=𝑣0=2 м/с, x0 =0. Следовательно, подставляя в (1.5) и (1.6) эти данные, получим:
c 1= 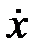0= 2 м/ с, c 2=0.
| (1.7) |
| (1.8) |
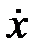= 0,21 t + 2,
x = 0,105 t2 + 2 t.
Уравнение (1.8) является уравнением движения автомобиля на участке АВ.
Определим время t 1движения автомобиля по этому участку, использовав условие, что при t= t 1, x = 𝑙1=20 м.
Следовательно, получим:
20= 0,105 
+ 2 
.
Или
0,105 + 2 . -20 = 0.
Откуда
t 1 
= 
.
Следовательно
t 1(1)=7,24 с, t 1(2)= - 26,28 с.
Из физических соображений t 1 > 0, поэтому принимаем t 1=7,24 с.
Подставив значение t 1 в уравнение (1.7), определим скорость автомобиля в точке В:
vВ = 0,21 t + 2 = 0,21∙7,24+2 = 3,52 м/с.
Рассмотрим движение автомобиля по участку ВС (рисунок 1.3).
Рисунок 1.3 - Расчетная схема для участка ВС
На данном участке на автомобиль действуют внешние силы: сила тяжести 
, нормальная реакция 
2, сила внешнего сопротивления 
2 (по условию задачи сила тяги F2 =0).
| (1.9) |
m(vCx – vBx) =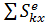 
,
| (1.10) |
= (G sinα2- R 2)Δ t = (G sinα2- R 2) t 2,
так как Δ t = t 2- 0= t 2.
Подставляя эти значения в (1.9), получим:
| (1.11) |
Откуда с учетом G = mg получим:
| (1.12) |
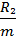) t 2.
Подставляя в (1.12) численные значения, находим:
vС =3,52+(9,81∙0,174 –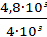 
)∙10=8,59 м/с.
Наконец, рассмотрим движение автомобиля по участку CD (рис.1.4).
Рисунок 1.4 – Расчетная схема для участка CD
На автомобиль действуют внешние силы: сила тяжести , реакция грунта 3, сила внешнего сопротивления 3 (по условию задачи сила тяги F3 =0).
Дифференциальное уравнение движения центра масс автомобиля на участке CD:
m =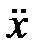 
= - R3 - G sinα 3.
Откуда с учетом G = mg
| (1.13) |
.
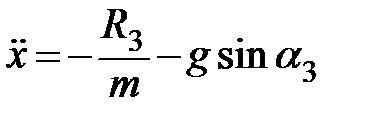По данным примера R 3=6кН, α 3=5°.
| (1.14) |
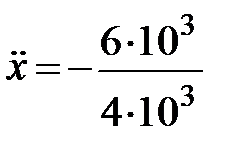= - 9,81∙0,087=-2,35 м/с2.
| (1.15) |
| (1.16) |
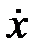=-2,35 t + c 5,
x = -1,17 t 2+ c 5+ c 6 .
Постоянные интегрирования определяем по начальным условиям при t =0, 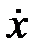0=𝑣 С = 8,59 м/с, x 0=0.
Подставив эти значения в (1.15) и (1.16), получим:
c 5=8,59 м/с, c 6= 0.
| (1.17) |
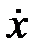= -2,35 t + 8,59,
| (1.18) |
Время движения автомобиля на участке CDt = t 3определяем из уравнения (1.17), пользуясь условием, что в точке D скорость vD = 0, т.к. автомобиль останавливается. Из (1.17) получаем:
0 =- 2,35 t 3+8,59.
Откуда t ₃= 
= 3,65 c.
Длину участка CD пути находим из уравнения (1.18), подставив в него время t=t 3:
𝑙 = - 1,17 t 2 +8,59 t = -1,17∙3,65+8,59∙3,65 = 15,77 м.
Пользуясь результатами расчетов, построим в соответствующих масштабах графики движения, скорости и ускорения автомобиля для каждого участка дороги.
Для построения названных графиков на участке АВ используем соответственно выражения (1.8), (1.7) и (1.4). При этом учтем, что время t нахождения автомобиля на этом участке изменяется от 0 до 7,24 с.
Для участка CD графики движения, скорости и ускорения определяются соответственно выражениями (1.18), (1.17) и (1.14). Заметим, при построении графиков отсчет времени t ведется с момента времени, соответствующего началу участка, то есть в точке С принимается t =0.
На участке ВС автомобиль движется равноускоренно с ускорением
| (1.19) |
= 
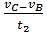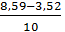= 0,507 м/с2.
| (1.20) |
| (1.21) |
𝑣2 = 3,52+0,507 t.
При этом время t изменяется от 0 до 10с.
В соответствии с зависимостями (1.4), (1.7), (1.8), (1.14), (1.17), (1.18), (1.19), (1.20) и (1.21) формируем массивы данных для построения графиков движения, скорости и ускорения автомобиля (таблица.1.2).
Таблица 1.2 – Массив данных для построения графиков движения, скорости и ускорения автомобиля
| Участок AB | t, c | 7,24 | |||||||||||
| x1 , м | 2,1 | 4,4 | 6,9 | 9,7 | 12,6 | 15,8 | 19,1 | ||||||
| 𝑣1, м/с | 2,21 | 2,42 | 2,63 | 2,84 | 3,05 | 3,26 | 3,47 | 3,52 | |||||
| a 1 м/с2 | 0,21 | ||||||||||||
| Участок BC | t, c | ||||||||||||
| x 2, м | 3,77 | 8,05 | 12,84 | 18,14 | 23,94 | 30,25 | 37,06 | 44,38 | 52,21 | 60,55 | |||
| 𝑣2, м/с | 3,52 | 4,03 | 4,53 | 5,04 | 5,55 | 6,05 | 6,56 | 7,07 | 7,58 | 8,08 | 8,59 | ||
| а 2, м/с2 | 0,507 | ||||||||||||
| Участок CD | t, c | 3,65 | |||||||||||
| x3, м | 7,42 | 12,5 | 15,24 | 15,77 | |||||||||
| 𝑣3, м/с | 8,59 | 6,24 | 3,89 | 1,54 | |||||||||
| a 3 м/с2 | -2,35 |
На рисунках 1.5, 1.6 и 1.7 сверху показаны графики движений автомобиля соответственно на участках АВ, ВС, и CD. Ниже на тех же рисунках изображены для этих движений графики скоростей и ускорений.
а)
б)
в)
Рисунок 1.5 – Графики движения (а), скорости (б) и ускорения (в) автомобиля на участке АВ пути
а)
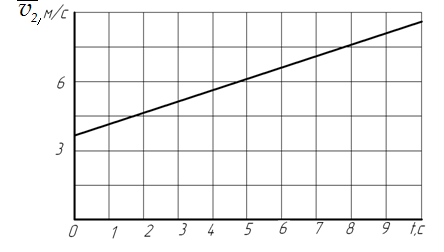
б)
в)
Рисунок 1.6 – Графики движения (а), скорости (б) и ускорения (в) автомобиля на участке ВС пути
а)
б)
в)
Рисунок 1.7 – Графики движения (а), скорости (б) и ускорения (в) автомобиля на участке CD пути
Автомобиль преодолевает участок АВ препятствия длины 20 м за 7,24с.
Совершает движение равноускоренно с ускорением a 1=0,21 м/с2. При этом скорость его возрастает от 2 до 3,52 м/с.
На участке ВС движение также равнопеременное, ускорение равно 0,507 м/с2. На этом участке скорость автомобиля изменяется от 3,52 м/с до 8,59 м/с. Автомобиль преодолевает данный участок длины 60,55 м за 10 с.
На участке CD сила тяги равна 0, автомобиль движется по инерции равнозамедленно до полной остановки в течение 3,65 с. При этом длина участка пути составляет 15,77м.
Содержание второго задания
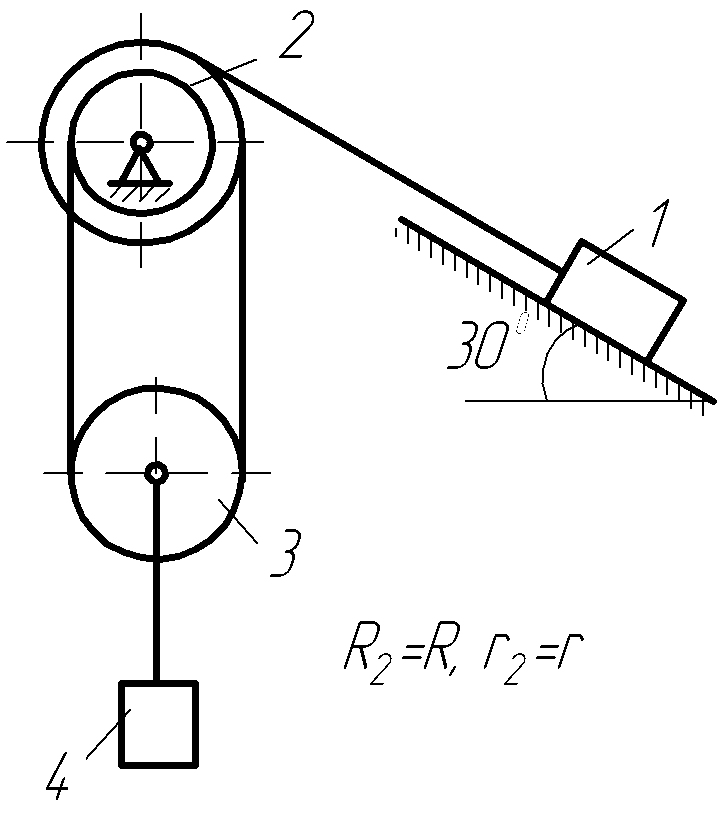
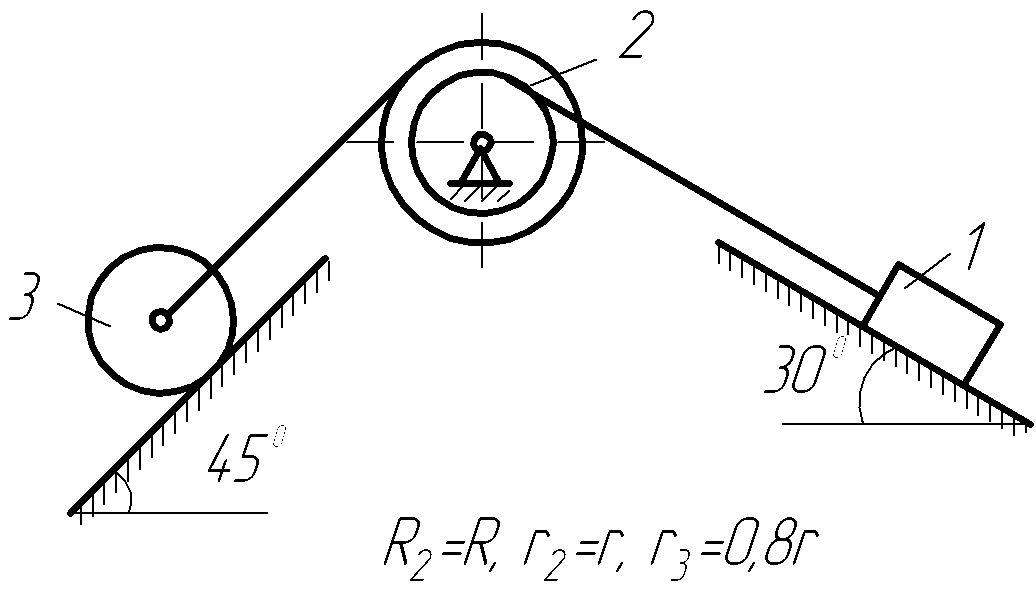
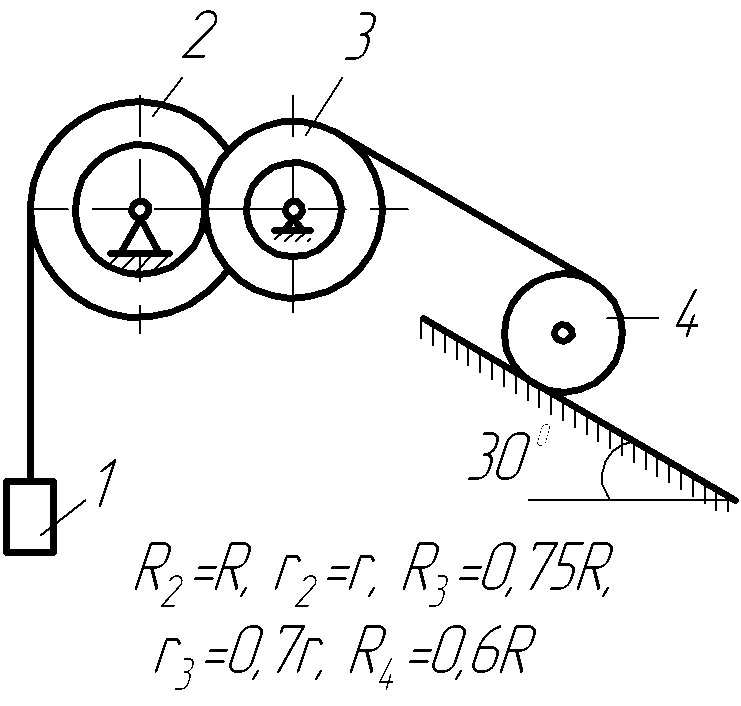
Механическая система, состоящая из трех или четырех тел, приходит в движение под действием сил тяжести из состояния покоя. Начальное положение системы показано на рисунках 2.1-2.5. Учитывая трение скольжения тела 1 (варианты 1, 3-6, 8-10, 16, 18, 21, 24, 26, 27, 29, 30) и тела 4 (варианты 7,12,13,22,23,25), а также трение качения тела 3 (варианты 2, 4, 6-8, 10, 12, 13, 17, 18, 22, 23, 25) и тела 4 (варианты 11, 14-16, 19, 20, 27-29), пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить:
1. Скорость тела 1 в тот момент времени, когда пройденный им путь станет равным S 1.
2. Ускорения тел, движущихся поступательно и ускорения центров масс тел, совершающих плоскопараллельное движение; угловые ускорения тел, совершающих вращательное и плоскопараллельное движения.
3. Реакции внешних и внутренних связей системы.
4. Выбрав в качестве обобщенной координаты пройденный телом 1 путь S и составив уравнение Лагранжа второго рода, найти зависимости 
= f 1(t), 
= f 2(t) и S= f 3(t). Полученные зависимости изобразить графически в пределах движения 0< S < S1 заданной системы.
Необходимые для расчета данные приведены в таблицах 2.1 и 2.2. Блоки и катки, радиус инерции которых в таблицах не указаны, считать однородными сплошными цилиндрами.
В задании приняты следующие обозначения: m 1, m 2, m 3, m 4 – массы тел 1, 2, 3, 4; i 2 x, i 3 x – радиусы инерции тел 2 и 3 относительно осей, проходящих через их центры масс перпендикулярно к плоскости движения; f – коэффициент трения скольжения; δ – коэффициент трения качения тела.
|
| ||
|
| ||
|
|
Рисунок 2.1
|
| ||
|
| ||
|
|
Рисунок 2.2
|
| ||
|
| ||
|
|
Рисунок 2.3
|
| ||
|
| ||
|
|
Рисунок 2.4
|
| ||
|
| ||
|
|
Рисунок 2.5
Таблица 2.1 – Исходные данные ко второму заданию
| Вар. № | m1 | m2 | m3 | m4 | i2x | i3x | f | δ,м |
| 8 m | 3 m | m | m | r 
| - | 0,2 | - | |
| 5 m | m | m | - | r
| - | - | 0,001 | |
| m | 5 m | m | m | r
| - | 0,2 | - | |
| 6 m | 2 m | m | - | 
| - | 0,1 | 0,001 | |
| 4 m | m | m | m | - | 1,5 
| 0,15 | - | |
| 3 m | m | 2 m | - | - | 1,2
| 0,2 | 0,001 | |
| 4 m | 2 m | m | m | - |
| 0,15 | 0,001 | |
| 4 m | m | 2 m | - | - | 1,5
| 0,1 | 0,0015 | |
| 8 m | 2 m | m | 2 m | - |
| 0,1 | - | |
| 5 m | m | m | - | 1,5
| - | 0,1 | 0,001 | |
| 6 m | 2 m | m | m |
| - | - | 0,0015 | |
| 4 m | 2 m | m | m |
| - | 0,2 | 0,0015 | |
| 6 m | m | 2 m | 4 m | - | 1,5
| 0,1 | 0,001 | |
| 2 m | m | 2 m | m |
| - | - | 0,001 | |
| 6 m | 3 m | 2 m | m |
| 1,5
| - | 0,0015 | |
| 8 m | 2 m | 3 m | m |
| 
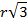
| 0,15 | 0,001 | |
| 5 m | m | m | - |
|
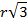
| - | 0,002 | |
| 4 m | 2 m | m | - |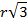
|
| 0,1 | 0,001 | |
| 6 m | 3 m | 2 m | m | 1,3
| 1,2
| - | 0,001 | |
| m | 2 m | m | m | 1,4
| - | - | 0,0015 | |
| 4 m | 2 m | m | m |
| - | 0,1 | - | |
| 3 m | 2 m | 2 m | m |
|
| 0,1 | 0,001 | |
| 4 m | m | m | 4 m | - |
| 0,1 | 0,0005 | |
| 8 m | m | 2 m | m | - |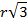
| 0,15 | - | |
| 8 m | 2 m | m | 3 m |
| - | 0,15 | 0,001 | |
| 8 m | m | 2 m | 2 m | 1,2
| - | 0,1 | - | |
| 4 m | m | m | m |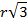
|
| 0,15 | 0,001 | |
| m | 3 m | 2 m | m |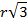
|
| - | 0,001 | |
| m | 3 m | 4 m | m |
| 1,4
| 0,1 | 0,0005 | |
| 8 m | m | m | m | - | 1,2
| 0,1 | - |
Таблица 2.2 – Дополнительные сведения ко второму заданию
| № группы | 
| m, кг | r, м | s₁,м |
| 0,30 | 1,0 | |||
| 2,25 | 0,22 | 0,8 | ||
| 0,25 | 0,5 | |||
| 1,75 | 0,35 | 0,3 | ||
| 2,5 | 0,20 | 0,6 | ||
| 2,75 | 0,27 | 0,4 |