Для изготовления пяти видов продукции используют три вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице:
| Вид ресурсов | Нормы расхода сырья на единицу продукции | Запасы | ||||
| I вид | II вид | III вид | IV вид | V вид | ||
| Сырье 1 | ||||||
| Сырье 2 | ||||||
| Производственная мощность | ||||||
| Прибыль |
Требуется найти такой план выпуска продукции, при котором будет максимальной общей стоимость продукции.
Экономико-математическая модель задачи будет иметь вид:
Целевая функция – это выражение, которое необходимо максимизировать:
Ограничения по ресурсам
Неравенство обращают в равенства, добавляя дополнительные переменные
Дополнительные переменные показывают количество соответствующего неиспользованного сырья, которое может остаться на складе.
Например,
х6 - количество неиспользованного сырья первого вида;
х7 - количество неиспользованного сырья второго вида;
х8 - неиспользованная мощность предприятия.
Дополнительные переменные х6 ,х7, х8 не способствуют увеличению прибыли, так как не участвуют в производстве, поэтому в функции цели F(x) эти переменные записываются с коэффициентом, равным нулю.
Составим симплекс таблицу:
В столбце сj записывают нули, так как за базис принимают дополнительные переменные, которые равны соответственно 2700, 1000,1000.
Таблица 1
| № с.-т. | сj | |||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | ||||||||||||
| Х7 | ||||||||||||
| Х8 |
В столбце xj xj проставляют коэффициенты при соответствующих неизвестных в уравнениях.
Значение последней строки F(x) получается при вычислении разности между суммой произведений элементов столбца Сj для базисных переменных на соответствующие элементы столбца xj (j=1, 2, …,8) и значением Сj в линейном функционале F(x) для данной переменной.
Найдем оценки столбцов по формуле:
Для следующих столбцов
Таблица 2
| № с.-т. | сj | |||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | ||||||||||||
| Х7 | ||||||||||||
| Х8 | ||||||||||||
| F(x) | -5 | -3 | -4 | -6 | -4 |
Переменную, которая находится в жирной колонки Таблицы 2., вводят в базис, так как она способствует большему увеличению прибыли.
Такой переменной в данном случае является Х4, у которой значение F(x) равно -6.
Чтобы выяснить, какую переменную необходимо удалить из базиса для введения Х4, находят положительные значения 
делением соответствующих элементов столбца Х0 на элементы ключевого столбца (на ноль и отрицательные числа ключевого столбца не делят).
Таблица 3
| № с.-т. | сj | 
| ||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | ||||||||||||
| Х7 | ||||||||||||
| Х8 |  5
| |||||||||||
| F(x) | -5 | -3 | -4 | -6 | -4 |
Среди выбирают наименьшее положительное (i =1, 2, 3- номера строк).
Ключевая строка показывает, что необходимо вывести переменную Х8.
После составления первоначальной программы приступают к следующей.
В таблицу 3 в базисе Х6, Х7, Х4 (введена вместо Х8 со значением С4 = +6).
Преобразуют ключевую строку, производя деление элементов ключевой строки на главный элемент Таблицы 3.
Результат записывают в шестую строку таблицы 3.
Это правило можно представить в виде формулы:
Заполняют шестую строку таблицы 4 для столбца Х0
где 1000 – элемент столбца Х0 в 3 строке;
4 – главный элемент, лежащий на пересечении 3 строки и 4 столбца.
Для небазисных переменных следующих столбцов:
Таблица 4
| № с.-т. | сj | |||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | ||||||||||||
| Х7 | ||||||||||||
| Х4 | 0,25 | 1,25 | 0,25 | 0,25 | ||||||||
| F(x) |
Остальные значения для других строк определяются по следующей формуле:
= 
- 
´ 
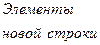Ключевой элемент преобразуемой строки лежит на пересечении преобразуемой строки и ключевого столбца (смотри Таблицу 3).
Элемент преобразованной ключевой строки берется в том же столбце Хj (j=1, 2, …,8), для которого определяют новый элемент в новой таблице 5.
Заполняют первую строку для базисной и небазисных переменных.
Таблица 4
| № с.-т. | сj | |||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | -5 | 1,5 | -6,5 | 0,5 | -2,5 | |||||||
| Х7 | ||||||||||||
| Х4 | 0,25 | 1,25 | 0,25 | 0,25 | ||||||||
| F(x) |
Аналогично вычисляют 5 строку:
Таблица 5
| № с.-т. | сj | |||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | -5 | 1,5 | -6,5 | 0,5 | -2,5 | |||||||
| Х7 | 2,5 | -1,5 | 2,5 | -0,5 | ||||||||
| Х4 | 0,25 | 1,25 | 0,25 | 0,25 | ||||||||
| F(x) |
Значение последней строки F(x) получается при вычислении разности между суммой произведений элементов столбца Сj для базисных переменных на соответствующие элементы столбца xj (j=1, 2, …,8) и значением Сj в линейном функционале F(x) для данной переменной.
Найдем оценки столбцов по формуле (таблица:
Для следующих столбцов
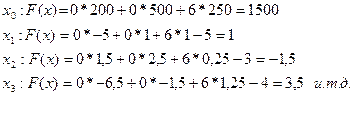
Таблица 6
| № с.-т. | сj | |||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | -5 | 1,5 | -6,5 | 0,5 | -2,5 | |||||||
| Х7 | 2,5 | -1,5 | 2,5 | -0,5 | ||||||||
| Х4 | 0,25 | 1,25 | 0,25 | 0,25 | ||||||||
| F(x) | -1,5 | 3,5 | -2,5 | 1,5 |
Переменную, которая находится в жирной колонки Таблицы 6., вводят в базис, так как она способствует большему увеличению прибыли.
Чтобы выяснить, какую переменную необходимо удалить из базиса для введения Х5, находят положительные значения делением соответствующих элементов столбца Х0 на элементы ключевого столбца (на ноль и отрицательные числа ключевого столбца не делят).
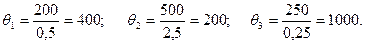
Таблица 7
| № с.-т. | сj |
| ||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | -5 | 1,5 | -6,5 | 0,5 | -2,5 | |||||||
| Х7 | 2,5 | -1,5 |  2,5
| -0,5 | ||||||||
| Х4 | 0,25 | 1,25 | 0,25 | 0,25 | ||||||||
| F(x) | -1,5 | 3,5 | -2,5 | 1,5 |
Среди выбирают наименьшее положительное (i =1, 2, 3- номера строк).
Ключевая строка показывает, что необходимо вывести переменную Х5.
После выбора ключевой строки и ключевого столбца переходим к заполнению следующей симплексной таблицы (Таблицы 8).
Необходимо отметить, что в ней значения линейной функции F(x) возрастает до 1500, причиной чего служит переменная Х4, которая вошла в базис.
Экономический смысл нового допустимого плана приведенного в таблице 8, состоит в том, что по нему рекомендуется производить продукцию Б4 в объеме 259 ед.
| № с.-т. | сj | |||||||||||
| Б | Х0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |||
| Х6 | -5,2 | -6,2 | -0,2 | -2,4 | ||||||||
| Х5 | 0,4 | -0,6 | 0,4 | -0,2 | ||||||||
| Х4 | 0,9 | 1,4 | -0,1 | 0,3 | ||||||||
| F(x) |
При переходе от одной симплексной таблице к другой возможны следующие случи:
1. Если F(x) имеет отрицательные числа, над которыми имеются положительные элементы, то программа требует улучшения;
2. Если F(x) имеет отрицательные числа нет положительных элементов, то максимум F(x) находится в бесконечности (задаче не решается);
3. Если нет не одного значения F(x)<0, то максимум F(x) достигнут (задача решена).
В Таблице 8 в строке F(x) нет отрицательных чисел, поэтому достигнут максимум F(x) при
Х5 =200;
Х4 =200.
Следовательно, если будут производить продукт Б5 и Б4 в объеме 200 ед., то получат максимальную прибыль в размере 2000руб;
Х6=100, значит что 100 кг. Сырья первого вида осталось не использованным.