Гидравлические элементы живого сечения потока в канале

ПЗ Равномерное движение жидкости в лотках

Формула Шези, скоростная и расходная характеристики

Уравнение равномерного движения позволяет преобразовать зависимости равномерного движения для расчета открытых русел. Скорость при этом определяется по формуле Шези

,

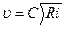С – коэффициент Шези;

R – гидравлический радиус.

Скоростная характеристика

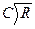=W.

Расход определяется

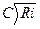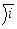Q=ωυ=ω =ωW =K .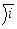

Расходная характеристика

ωW=K.

Для каналов, в которых жидкость движется в турбулентном режиме, применяется формула Павловского

,

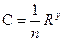n – шероховатость канала, зависящий от материала стенок и дна;

R – гидравлический радиус;

y – показатель степени.

Частным случаем является формула Маннинга

.

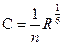Расход с учетом формулы Павловского определится

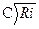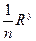
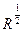
Q=ω 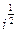=ω = ω = ,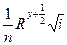

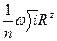z=y+0,5 – показатель степени.

 

Приближенно можно по Н.Н. Павловскому считать:

при R < 1,0 м у = 1,5,

при R > 1,0 м y = 1,3.

 

Гидравлические элементы живого сечения потока в канале

 

1. Симметричное трапецеидальное поперечное сечение (рис.6.2,а).

Здесь b – ширина канала по дну; h – глубина наполнения канала; величина m, указаная на чертеже, – коэффициент откоса

.

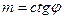Угол ψ (рис.6.2,а) задают не по соображениям гидравлического расчета, а, учитывая устойчивость грунта откоса (если откосы канала образуются нескальным грунтом). Ширина потока по верху

.

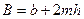Величины живого сечения ω и смоченного периметра χ удобно вычислять по следующим геометрическим зависимостям

;

 

.

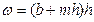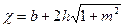Зная ω и χ, определяем величину R

.

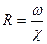1. Определить расход при равномерном движении воды в трапецеидальном земляном канале (суглинок), если ширина его по дну b =5,5 м, глубина h =1,8 м, заложение откосов т= 1 и уклон i =0,0004.

Решение.

Скорость определяем по формуле Шези

υ=C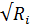

Площадь живого сечения

ω=(b +mh) h= (5,5 + 1*1,8) 1,8=13,14 м².

Смоченный периметр

χ = b + 2h 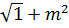=5,5+2*1,8 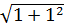=10,58 м.

Гидравлический радиус

R = ω / χ = 13,14/10,58 =1,24 м.

Определяем коэффициент С по формуле Павловского. Коэффициент шероховатости n =0,025. Поскольку R= 1,24 м>1 м, то

у =1.3 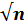= 1,3* 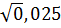= 0,206.

Тогда

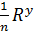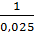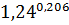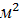C= = * =41,8 /c

Скорость

υ = С 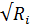= 41,8 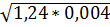= 0,93 м/с.

Сравним полученную скорость с максимальной неразмывающей средней скоростью и наименьшей допустимой незаиляющей скоростью. Первая для каналов в средних суглинках равна 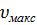= 1м/с. Вторую определим по формуле

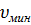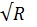= 0,5 = 0,5 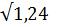= 0,56 м/с.

Так как 0,56 м/с<0,93 м/с<1 м/с, то канал размыву и заилению подвергаться не будет.

Расход воды

Q = υ ω = 13,14 0.93= 12,2 м³/с.

 

 

2. Определить, будет ли устойчив против размыва треугольный водосточный лоток автомобильной дороги, мощенный булыжником ( n =0,02 =3 м/с), если заложение откосов m₁ =0,5 и m₂ =2; глубина воды h =0,18 м, а уклон лотка i= 0,004.

Решение. Определяем скорость движения воды в лотке по формуле (6.1). Живое сечение

ω = 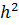(m₁ + m₂) = 0,18*(0,5+2)=0,04м.

Смоченный периметр

χ=h( 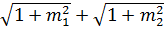)= 0,18 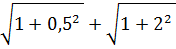=0,6м.

Гидравлический радиус

R=ω/χ =0,04/0,6 = 0,066 м.

Определяем коэффициент Шези С по формуле Маннинга. Принимаем коэффициент шероховатости n =0,02. Тогда

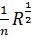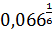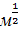С = =1/0,02* =31,8 /c

Скорость

υ= 31,8 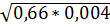= 0,52 м/с.

Допускаемая скорость на размыв в лотках с одиночной мостовой 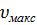=3 м/с. Поскольку 0,52 м/с<3 м/с, лоток размываться не будет.

3. Определить уклон i водосточного коллектора прямоугольного сечения шириной b =1,4 м, который обеспечивал бы при глубине h =l,3 м пропуск расхода Q =2,l м³/с. Коллектор выполнен из сборного железобетона n =0,015.

 

 

4. Бетонный канал трапецеидального сечения, предназначенный для пропуска расхода воды Q =7,5 м³/с, по гидрогеологическим условиям может иметь глубину не более h =1,2 м. Определить ширину канала b, необходимую для пропуска заданного расхода, при уклоне i =0,0004 и заложении откосов m =1.

Решение. Задачу решаем подбором. Находим модуль расхода для заданного Q

Задаваясь различными значениями ширины канала, вычисляем соответст­вующие модули расхода по формуле

Результаты расчетов сводим в таблицу

 

b,м	ω,м	χ,м	R,м	С, /c.	К, м3/с

 

 

По данным расчетов построен график зависимости K=f(b)