Если система незамкнутая, т.е. действует внешняя сила F, то можно показать, что полная механическая энергия не сохраняется, а ее изменение
ΔW = AF,
где АF — работа внешней силы.
Рассмотрим систему тел (тело—Земля), на которую действует внешняя сила F. Пусть тело поднимают вверх на высоту h (рис. 14.1).

Рисунок 14.1. Система «тело – Земля».
Работа внешних сил
АF = Fh.
Работа внутренней силы (силы тяжести)
Amg = -mgh = -ΔWn.
Согласно теореме о кинетической энергии
ΔWK = А,
где А — суммарная работа всех сил, действующих на тело:
А = AF + Amg.
Следовательно,
ΔWK = -ΔWn + AF=>ΔW = AF.
Закон сохранения и превращения энергии
Если в замкнутой системе между телами действует сила трения, то полная механическая энергия убывает и, как показывает опыт, ее изменение равно работе силы трения:
ΔW = ATP.
Не сохраняется полная механическая энергия и в том случае, если в системе тел происходят неупругие деформации. Но убывание механической энергии не означает, что энергия исчезает бесследно. Она превращается из механической в другую, в частности во внутреннюю энергию.
Для любой замкнутой системы всегда выполняется закон сохранения и превращения энергии: величина полной энергии (механической и другой) замкнутой системы остается постоянной. При этом, будучи несозидаемой и неуничтожаемой, энергия может превращаться из одного вида в другой.
Упругие и неупругие соударения тел
Примером применения законов сохранения импульса и энергии является соударение (удар) тел.
Удар — это кратковременное взаимодействие соприкасающихся тел, приводящее к значительному изменению состояния их движения.
Тела во время удара претерпевают деформацию. Кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в потенциальную энергию упруго деформированных тел. За время удара происходит перераспределение энергии между соударяющимися телами.
Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс.
Различают два предельных типа удара:
а) удар абсолютно упругий,
б) удар абсолютно неупругий.
Абсолютно упругим называется удар, после которого возникшие в телах деформации полностью исчезают.
При абсолютно упругом ударе выполняются закон сохранения импульса и закон сохранения механической энергии.
Абсолютно неупругий удар — удар, после которого возникшие в телах деформации полностью сохраняются.
После абсолютно неупругого удара тела движутся как единое целое. Такой удар наблюдается при столкновении тел из мягких, пластичных материалов.
При абсолютно неупругом ударе выполняется только закон сохранения импульса, а кинетическая энергия тел не сохраняется.
Простейшие механизмы
Для облегчения совершения механической работы издавна используются различные приспособления — простые механизмы.
Простые механизмы — это устройства, в которых работа совершается только за счет механической энергии.
Простые механизмы (рычаг, наклонная плоскость, блок и др.) служат для преобразования силы, их применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Наклонная плоскость.
Ее используют в тех случаях, когда надо поднять тяжелый груз на некоторую высоту.
Рассмотрим гладкую наклонную плоскость (рис. 17.1).
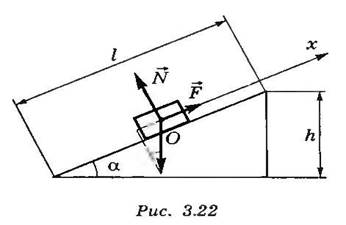
Рисунок 17.1. Наклонная плоскость.
Рассчитаем силу F, которую надо приложить к телу массой m, чтобы поднять его равномерно на высоту h.
Запишем основное уравнение динамики:
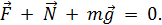
Спроецируем это равенство на ось Ox:
F- mgsinα = 0.
Отсюда искомая сила
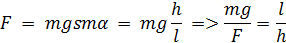
т.е для равномерного поднятия груза с помощью наклонной плоскости необходимо приложить силу, во столько раз меньшую силы тяжести груза, во сколько раз длина наклонной плоскости больше ее высоты.
Рычаг.
Рычагом называют имеющее неподвижную ось вращения твердое тело, на которое действуют силы, стремящиеся повернуть его вокруг этой оси. Различают рычаги первого и второго рода.
Рычагом первого рода называют рычаг, ось вращения О которого расположена между точками А и В приложения сил, а сами силы направлены в одну сторону (рис. 17.2, а). Это коромысло равноплечих весов, железнодорожный шлагбаум, ножницы и др.
Рычаг второго рода — рычаг, ось вращения О которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу (рис. 17.2, б). Это гаечные ключи, щипцы для раскалывания орехов, двери и др.

Рисунок 17.2. а) рычаг первого рода; б) рычаг второго рода.
Условие равновесия рычага вытекает изправила моментов М1 = М2.
Так как
М1 = F1l1 и М2= F2l2,
где l1 иl2 — плечи сил, действующих на рычаг, тоусловие равновесия рычага имеет вид:

При равновесии рычага под действием двух сил модули этих сил обратно пропорциональны их плечам.
С помощью рычага можно получить выигрыш в силе, т.е. меньшей силой можно уравновесить большую силу.
Блок.
Блоки используют для поднятия грузов. Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускают веревку, трос или цепь. Неподвижным называют такой блок, ось которого закреплена и при подъеме грузов она не поднимается и не опускается (рис. 17.3, а, б).

Рисунок 17.3. Неподвижный блок.
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи приложенных сил равны радиусу колеса. Следовательно, из правила моментов
mgr = Fr
вытекает, что неподвижный блок выигрыша в силе не дает (F=mg). Он позволяет менять направление действия силы.
На рисунке 17.4, а, б изображен подвижный блок (ось блока поднимается и опускается вместе с грузом).
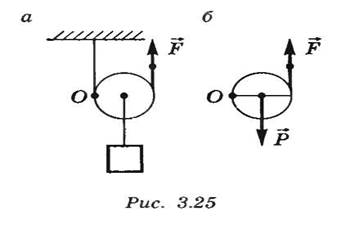
Рисунок 17.4. Подвижный блок.
Такой блок поворачивается около мгновенной оси О. Правило моментов для него будет иметь вид:
mgr = F•2r => 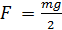
Таким образом, подвижный блок дает выигрыш в силе в два раза.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 17.5). Неподвижный блок применяется только для удобства. Он, изменяя направление действия силы, позволяет, например, поднимать груз, стоя на земле.

Рисунок 17.5. Совместное использование подвижного и неподвижного блоков.