Закон сохранения импульса

ВВЕДЕНИЕ

Данное учебное пособие имеет целью оказать учащимся помощь в систематизации, обобщении и углублении знаний по физике, освоении методов и приемов решения задач при подготовке к итоговой аттестации.

Содержание учебного пособия соответствует программе по физике для студентов первого курса, обучающихся по специальностям 151901 Технология машиностроения, 190631 Техническое обслуживание и ремонт автомобильного транспорта, 260807 Технология продукции общественного питания.

Данное пособие включает:

· перечень рассматриваемых вопросов;

· систематизированное изложение основного теоретического материала (ориентирует учащихся на усвоение понятий, законов, закономерностей и т.д.);

· вопросы и задания для самоконтроля (они подобраны и сформулированы так, чтобы учащиеся могли проверить уровень своих знаний и умений по теме; вопросы и задания постепенно усложняются, что требует от учащихся для ответа и решения глубокого понимания физических законов, явлений и процессов, привлечения знаний из различных разделов физики);

· методические рекомендации по решению задач (последовательность действий, которые необходимо выполнить при решении задач, - от анализа условия задачи (его краткой записи, выполнение рисунка, схемы, чертежа, поясняющих условие задачи) до анализа и оценки полученного ответа);

· примеры решения задач (на примере решения наиболее типовых задач демонстрируется процесс построения и использования алгоритма решения задач на основе методических рекомендаций).

В приложении приведены тест и вариант контрольной работы, которую учащиеся выполняют самостоятельно.

Роль законов сохранения в механике и в других разделах физики огромна. Во-первых, они позволяют сравнительно простым путем, не рассматривая действующие на тела силы, решать ряд практически важных задач. Законы сохранения позволяют по первоначальному состоянию системы, не зная подробностей взаимодействия тел, определить ее конечное состояние, например, зная скорости тел до взаимодействия, определить скорости этих тел после взаимодействия. Во-вторых, и это главное, открытые в механике законы сохранения играют в природе огромную роль, далеко выходящую за рамки самой механики. Даже в тех условиях, когда законы механики Ньютона применять нельзя, законы сохранения импульса, энергии и момента импульса не теряют значения. Они применимы как к телам обычных размеров, так и к космическим телам и элементарным частицам. Именно всеобщность законов сохранения, их применимость ко всем явлениям природы, а не только к механическим делает эти законы столь значительными.

ЗАКОНЫСОХРАНЕНИЯ В МЕХАНИКЕ

Импульс тела. Импульс силы. Закон сохранения импульса. Реактивное движение. К. Э. Циолковский — основоположник учения о реактивном движении.

Механическая работа. Работа силы тяжести, силы упругости, силы трения. Мощность.

Механическая энергия. Кинетическая и потенциальная энергия. Потенциальная энергия тел при гравитационном взаимодействии. Потенциальная энергия упруго деформированного тела. Закон сохранения энергии в механике. Изменение энергии в незамкнутых системах. Закон сохранения и превращения энергии. Упругие и неупругие соударения тел.

Импульс тела

Импульсом тела (количеством движения) называется векторная физическая величина, равная произведению массы тела т на его скорость и направленная так же, как и скорость (рис. 1.1):

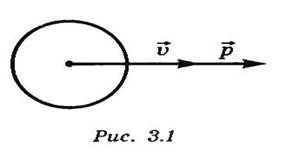
Рисунок 1.1 Импульс тела.

(1.1)

Единицей импульса тела в СИ является килограмм-метр на секунду

Пусть скорость тела под действием силы F изменяется за время Δt от v₀ до v. Согласно основному уравнению динамики

Учитывая, что

получим

(1.2)

Произведение силы на время ее действия называется импульсом силы. Единицей импульса силы является ньютон-секунда (Н с).

Формула (1.2) выражает второй закон Ньютона, который может быть сформулирован следующим образом: изменение импульса тела равно им пульсу равнодействующей сил, действующих на данное тело.

Отсюда видно, что импульс тела изменяется под действием данной силы одинаково у тел любой массы, если только время действия сил одинаково.

Импульс тела, как и скорость, зависит от выбора системы отсчета. Ускорение движения тела одинаково во всех инерциальных системах отсчета. Следовательно, сила, а значит, согласно (1.2) и изменение импульса тела не зависит от выбора системы отсчета. В любой инерциальной системе отсчета изменение импульса тела одинаково.

Закон сохранения импульса

Рассмотрим систему трех тел (рис. 2.1).

На тела действуют внешние силы F₁, F₂, F₃. Силы F_l2, F₂₁,F₁₃,F₃₁, F₂₃, F₃₂ — внутренние силы.

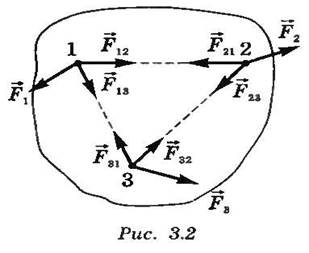
Рисунок 2.1. Система трех тел.

Запишем для каждого тела основное уравнение динамики:

Просуммировав эти уравнения и учитывая, что согласно третьему закону Ньютона

получим

где — импульс системы тел.

Импульс системы тел равен геометрической сумме импульсов тел системы. Таким образом, импульс системы тел могут изменить только внешние силы. Если система замкнута, то

(2.1)

Равенство (2.1) выражает закон сохранения импульса (ЗСИ): импульс замкнутой системы тел сохраняется при любых взаимодействиях этих тел.

В случае незамкнутой системы ЗСИ используется, если:

а) геометрическая сумма внешних сил равна нулю;

б) проекция равнодействующей внешних сил на некоторое направление равна нулю, т.е. вдоль этого направления импульссистемы сохраняется;

в) время взаимодействия мало (выстрел, взрыв, удар и т.п.).

С помощью ЗСИ можно вычислять скорости тел, не зная значения сил, действующих на них. ЗСИ является всеобщим законом: он применим как к телам обычных размеров, так и к космическим телам и элементарным частицам.

Реактивное движение

Под реактивным движением понимают движение тела, возникающее при отделении от тела его части с некоторой относительно тела скоростью.

При этом появляется так называемая реактивная сила, толкающая тело в сторону, противоположную направлению движения отделяющейся от него части тела.

Реактивное движение совершает ракета (рис. 3.1). Основной частью реактивного двигателя является камера сгорания. В одной из ее стенок имеется отверстие — реактивное сопло, предназначенное для выхода газа, образующегося при сгорании топлива. Высокая температура и давление газа определяют большую скорость истечения его из сопла.

До работы двигателя импульс ракеты и горючего был равен нулю, следовательно, и после включения двигателей геометрическая сумма импульсов ракеты и истекающих газов равна нулю:

где m и — масса и скорость выбрасываемых газов, М и — масса и скорость ракеты.

Рисунок 3.1. Реактивное движение.

В проекции на ось Оу:

— скорость ракеты.

Эта формула справедлива при условии небольшого изменения массы ракеты.

Конечная скорость ракеты находится в соответствии с формулой Циолковского:

(3.1)

Где – отношение начальной и конечной масс ракеты.

Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости υ=7,9·10³м/с при =3·10³м/с (скорости истечения газов при сгорании топлива бывают порядка 2–4км/с) стартовая масса одноступенчатой ракеты должна примерно в 14раз превышать конечную массу. Для достижения конечной скорости υ₂=4 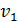отношение М₀/М должно быть равно 50.

Значительное снижение стартовой массы ракеты может быть достигнуто при использовании многоступенчатых ракет, когда ступени ракеты отделяются по мере выгорания топлива. Из процесса последующего разгона ракеты исключаются массы контейнеров, в которых находилось топливо, отработавшие двигатели, системы управления ит.д. Именно по пути создания экономичных многоступенчатых ракет развивается современное ракетостроение.

Главная особенность реактивного движения состоит в том, что ракета может как ускоряться, так и тормозиться и поворачиваться без какого-либо взаимодействия с другими телами в отличие от всех других транспортных средств.

По принципу реактивного движения передвигаются осьминоги, кальмары, каракатицы, медузы.

Большая заслуга в развитии теории реактивного движения принадлежит К. Э. Циолковскому. Он разработал теорию полета тела переменной массы (ракеты) в однородном поле тяготения и рассчитал запасы топлива, необходимые для преодоления силы земного притяжения, основы теории жидкостного реактивного двигателя, а также элементы его конструкции, теорию многоступенчатых ракет, причем предложил два варианта: параллельный (несколько реактивных двигателей работает одновременно) и последовательный (реактивные двигатели работают друг за другом). К. Э. Циолковский строго научно доказал возможность полета в космос с помощью ракет с жидкостным реактивным двигателем, предложил специальные траектории посадки космических аппаратов на Землю, выдвинул идею создания межпланетных орбитальных станций, предложил идею автоматического управления ракетой.

Труды К. Э. Циолковского явились теоретической базой для развития современной ракетной техники.

Механическая работа

Действие силы, связанное с перемещением тела, характеризуется механической работой.

Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы на модуль перемещения и на косинус угла между ними:

A= FΔrcosa.

В СИ единицей работы является джоуль (Дж).

Здесь F = const и а = const на всем перемещении (рис. 4.1).

Рисунок 4.1. Работа при перемещении тела.

Работа — величина скалярная и может быть как положительной, так и отрицательной (рисунок 4.2).

Рисунок 4.2. Зависимость работы от направления действия силы.

В общем случае сила переменна, путь криволинеен, угол α изменяется произвольно. Тогда для определения работы нужно мысленно разбитьвсе перемещение 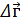на такие малые перемещения , на которых можно считать силу и угол неизменными, и найти элементарные работы по формуле

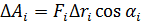
Работа на всем перемещении будет равна алгебраической сумме элементарных работ и тем точнее, чем меньше каждое перемещение и чем больше их число:

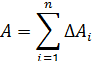
и в пределе при Δг→0

Работа силы F на всей траектории выражается интегралом, вычисляемым вдоль траектории, где 1 и 2 — радиус-векторы начальной и конечной точек траектории.

Для вычисления этого интеграла надо знать зависимость F(r) вдоль траектории. Для определения работы можно воспользоваться графическим методом (рис. 4.3, а, б, в).

Рисунок 4.3. Графический метод для определения работы.

На графике F_x= f(x) работа на перемещении Δr_х = Δx численно равна площади заштрихованной фигуры. Работу можно представить как произведение средней силы на перемещение:

А = <F>Δг.

В частности, если сила изменяется линейно от F₁ до F₂ на данном перемещении, то ее среднее значение

и тогда работу можно рассчитать по формуле

Если к движущемуся телу приложено несколько сил, то каждая из них совершает работу, а общая работа равна алгебраической сумме работ, совершаемых отдельными силами.

Работа силы тяжести

Пусть тело перемещается вертикально вниз из положения 1 в положение 2, определяемые соответственно высотами h₁иh₂ над нулевым уровнем (рис. 5.1).

Рисунок 5.1. Работа силы тяжести.

Работа силы тяжести

При перемещении тела из положения 1 в положение 2 по траектории 1—3—2 работа силы тяжести

А = А₁₃ + А₃₂.

Но

A_l₃ = mgΔr₁cosα, A₃₂ = mgΔr₂cos90° = 0.

Из рисунка 5.1 видно, что

Δr₁cosα=h₁-h₂ =>A=mg(h_l~h₂).

Это значит, что работа силы тяжести не зависит от формы траектории движения тела, а зависит только от перемещения центра тяжести тела по вертикали. На замкнутой траектории работа силы тяжести равна нулю.

Силы, работа которых не зависит от формы траектории, а на замкнутой траектории равна нулю, называются консервативными. Следовательно, сила тяжести — консервативная сила.

Работа силы упругости

Пусть тело, прикрепленное к пружине и находящееся на гладком стержне, перемещается из положения 1 в положение 2 (рис. 6.1).

Рисунок 6.1. Движение тела на пружине.

Сила упругости, действующая на тело со стороны деформированной пружины, не остается постоянной, а изменяется согласно закону Гука пропорционально абсолютному удлинению:

F₁ =kx₁ и F₂ = kx₂.

Найдем работу силы упругости на этом перемещении по формуле

Более строгий вывод формулы для расчета работы силы упругости можно сделать, использовав метод интегрирования:

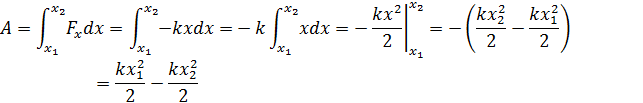
Можно показать, что работа силы упругости не зависит от формы траектории и на замкнутой траектории равна нулю. Она зависит только от взаимного положения частей тела. Сила упругости тоже консервативная сила.

Работа силы трения

Так как сила трения направлена противоположно перемещению (рис. 7.1), то работа силы трения будет

А_тр = F_TPΔг cos 180° = -F_TPΔr.

Рисунок 7.1. Сила трения направлена противоположно движению тела.

Пусть тело перемещается из точки 1 в точку 2 по разным траекториям. Так как модули перемещений Δг₁ и (Δг₂ + Δг₃) неодинаковы (рис. 7.2), то сила трения совершает разные работы.

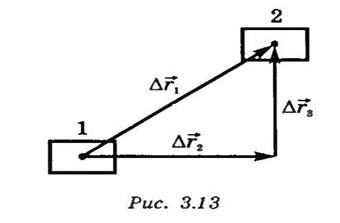
Рисунок 7.2. Перемещение тела по разным траекториям.

Таким образом, в отличие от силы тяжести и силы упругости работа силы трения зависит от формы траектории, по которой движется тело, и на замкнутой траектории не равна нулю. Работа силы трения необратимо превращает механическое движение тела в тепловое движение атомов и молекул.

Мощность

Различные машины и механизмы, выполняющие одинаковую работу, могут отличаться мощностью. Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.

При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.

Средняя мощность силы — скалярная физическая величина N, равная отношению работы А, совершаемой силой, к промежутку времени Δt, в течение которого она совершается:

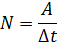
В СИ единицей мощности является ватт (Вт).

Если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу А = FΔrcosα. Поэтому мощность этой силы

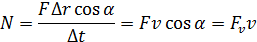
где — проекция силы на направление движения.

По этой формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значения средней или мгновенной скорости.

Мгновенная мощность — это мощность силы в данный момент времени.

Любой двигатель или механизм предназначены для выполнения определенной механической работы, которую называют полезной работой А_п. Но любой машине приходится совершать большую работу, так как вследствие действия сил трения часть подводимой к машине энергии не может быть преобразована в механическую работу. Поэтому эффективность работы машины характеризуют коэффициентом полезного действия (КПД).

Коэффициент полезного действия η — это отношение полезной работы Ап, совершенной машиной, ко всей затраченной работе А₃ (подведенной энергии W):

где N_n, N₃ — полезная и затраченная мощности соответственно.

КПД обычно выражают в процентах.

Механическая энергия

Механическое состояние тела (системы тел) определяется его положением относительно других тел (координатами) и его скоростью.

Если изменяется хотя бы одна из этих величин, то говорят об изменении механического состояния тела.

Состояние данной системы тел обязательно изменяется, если внешние силы совершают отличную от нуля работу.

Количественно механическое состояние системы и его изменение характеризуется механической энергией W.

Механическая энергия — это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу.

Изменение механической энергии ΔW равно работе приложенных к системе внешних сил:

ΔW = А.

Значение энергии системы в данном состоянии не зависит от пути перехода ее в это состояние.

Кинетическая энергия

Найдем, как энергия тел зависит от их скорости.

Пусть на тело массой m действуетсила F (это может быть одна сила или равнодействующая нескольких сил), направленная вдоль перемещения, и скорость тела изменяется от 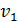до (рис. 10.1).