При решении задач на закон сохранения импульса необходимо:
1.Указать, какие тела входят в рассматриваемую систему. Сделать рисунок, изобразив на нем векторы импульсов тел непосредственно перед и после взаимодействия. Если направление искомого импульса заранее неизвестно, то для него принимается некоторое условное направление
2. Выяснить, является система замкнутой или нет.
Если система замкнута или выполняется одно из следующих условий:
а) внешние силы уравновешиваются,
б) время взаимодействий мало,
в) проекция равнодействующей внешних сил на какое-то направление (ось Ох) равна нулю, то записать закон сохранения импульса:

или для последнего случая ^

Если система незамкнута, то записать

рассматривая движение всех тел системы в одной и той же инерциальной системе отсчета.
3. Спроецировать записанные уравнения на выбранные оси координат Ох и Оу.
4. Дополнить при необходимости систему полученных уравнений кинематическими и динамическими уравнениями.
При решении задач на вычисление работы постоянной силы необходимо:
1.Выяснить, работу какой силы требуется определить в задаче, и записать исходную формулу
А = FΔrcosα.
2. Сделать рисунок, указав на нем силы, приложенные к телу, и вектор перемещения, а также определить угол между данной силой и перемещением.
3. Если сила не задана, найти ее из основного уравнения динамики.
4. Найти перемещение (если оно не задано) из кинематических уравнений.
5. Подставить значения силы и перемещения в формулу работы.
6. При расчете работы переменной силы проще воспользоваться графическим способом.
При решении задач на определение мощности необходимо:
1.Выяснить, какую мощность нужно определить — среднюю или мгновенную.
2. Записать формулы для расчета мощности:

Первая из них позволяет рассчитать среднюю мощность, а вторая и третья — как среднюю, так и мгновенную в зависимости от того, подставляют ли значение средней скорости или мгновенной.
3. Из основного уравнения динамики определить силу тяги, сделав предварительно рисунок с указанием действующих на тело сил.
4. Из законов кинематики определить среднюю или мгновенную скорости, если они не заданы в условии задачи.
5. Подставить найденные значения силы тяги и скорости в формулу для расчета мощности.
При решении задач на применение закона превращения и сохранения энергии необходимо:
1.Сделать схематический рисунок, отметив на нем начальное и конечное положения тел (1 и 2), указанные в задаче.
2. Выбрать нулевой уровень отсчета потенциальной энергии.
3. Указать скорости и высоты (или координаты тела, движущегося под действием силы упругости), характеризующие состояние тела в обоих положениях.
4. Записать формулу для расчета полной механической энергии в положениях 1 и 2.
5. Выяснить, какие силы в рассматриваемой механической системе являются внешними, внутренними, консервативными, неконсервативными.
6. Для замкнутой системы, в которой действуют только консервативные силы, записать закон сохранения механической энергии
Wl = W2.
Если в замкнутой системе действуют силы трения, записать формулу
W2-Wl=ATP.
Если система незамкнута и внешние силы совершают работу А, то
W2-W1=A.
7. Написать формулы для расчета работы А или Атр.
8. Составить при необходимости дополнительные уравнения из динамики или кинематики. В некоторых задачах надо применить и закон сохранения импульса.
9. Решить полученную систему уравнений.
ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
Задача 1.
Шарик массой m, летящий со скоростью v, ударяется о стенку под углом α к ней и отскакивает под тем же углом без потери скорости. Определите направление и модуль вектора изменения импульса шарика за время удара.
Дано: m, v, α.
Найти: Δр.
Решение.

Так как импульс — величина векторная, то искомое изменение импульса шарика равно геометрической разности конечного и начального значений импульса:

Учитывая, что модуль скоростей не изменяется, т.е.

Из рисунка находим модуль изменения импульса:

Задача 2.
Кубик из пенопласта массой 100 г лежит на горизонтальной подставке. Высота кубика 10 см. Снизу кубик пробивает вертикально летящаяпуля массой 10 г. Скорость пули при входе в кубик 100 м/с, при вылете — 95 м/с. Подпрыгнет ли кубик?
Дано: m1 =0,100 кг, h = 0,10 м, m2 = 0,010 кг,v1 = 100 м/с, v2= 95 м/с.
Найти: F.
Решение. Кубик подпрыгнет, если модуль силы, действующей на кубик со стороны пули, будет больше его силы тяжести F > m1g.

Для нахождения этой силы, рассмотрим пулю. На нее действует сила тяжести и со стороны кубика сила F', равная по модулю согласно третьему закону Ньютона силе F.
Запишем второй закон Ньютона в импульсной форме:

или в проекции на ось Оу:

Считая, что пуля внутри кубика движется равнозамедленно, можно найти время:

Подставим во второй закон Ньютона:

откуда

Подставив численные значения, получим F= 50 Н. Следовательно, кубик подпрыгнет, так как m1g= 1,0 Н.
Задача 3.
В результате взрыва камень разлетается на три куска. Два куска летят под прямым углом друг к другу: кусок массой 1,0 кг — со скоростью 12 м/с, кусок массой 2,0 кг — со скоростью 8,0 м/с. Третий кусок отлетает со скоростью 40 м/с. Какова масса третьего куска и в каком направлении он летит?
Дано: m1 = 1,0 кг, v1=12 м/с, m2 = 2,0 кг, v2 = 8,0 м/с, v3 = 40 м/с.
Найти: m3, α.
Решение. Система "камень—куски" незамкнута вследствие действия силы тяжести. Однако задача может быть решена на основании ЗСИ, так как время разрыва мало. До разрыва камень покоился, поэтому импульс его был равен нулю.

После разрыва импульсы кусков соответственно p1, р2, р3. Запишем ЗСИ:

Геометрическая сумма импульсов первых двух кусков

Из ЗСИ

Следовательно,

Из рисунка находим по теореме Пифагора
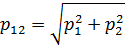
Поэтому

Следовательно,


Подставим численные значения, получим: m3=0,50 кг; tgα = 0,75; α = 53°.
Задача 4.
Мальчик, бегущий со скоростью 4,0 м/с, догоняет тележку, движущуюся со скоростью 3,0 м/с, и вскакивает на нее. Масса мальчика 50 кг,тележки 80 кг. Найдите скорость тележки в тот момент, когда на нее вскочил мальчик.
Дано: v1 = 4,0 м/с, v2=3,0 м/с, m1 = 50 кг, m2= 80 кг.
Найти: v.
Решение. Рассмотрим систему "мальчик—тележка". Поскольку силы взаимодействия мальчика и тележки с Землей не имеют составляющих в горизонтальном направлении, то для горизонтальных составляющих импульсов можно записать ЗСИ.

До взаимодействия импульс мальчика равен  , импульс тележки равен
, импульс тележки равен 
По закону сохранения импульса

или в проекции на ось Ох:

Задача 5.
Вертолет, масса которого с грузом 6,0•103 кг, за 2,5 мин набралвысоту 2250 м. Определите работу двигателя за это время, считая подъем вертолета равноускоренным.
Дано: m= 6,0•103 кг, t= 1,5•102 с, h = 2250 м.
Найти: А.
Решение. Искомая работа
A=Fh,
где F — сила тяги двигателя. Для ее нахождения рассмотрим, какие силы действуют на вертолет:
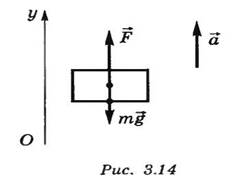
сила тяги F и сила тяжести mg.
Основное уравнение динамики:

В проекции на ось Оу:
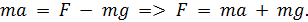
При равноускоренном движении пройденный путь


Искомая работа

Задача 6.
К лежащему на горизонтальной поверхности бруску массой 12 кгприкреплена невесомая пружина жесткостью 300 Н/м. Коэффициент трения между бруском и поверхностью 0,40. К свободному концу пружины приложена внешняя сила под углом 30° к горизонту, под действием которой груз равномерно перемещается на расстояние 4,0 м. Определите работу, совершенную внешней силой.
Дано: m = 12 кг, k = 300 Н/м, μ = 0,40, α = 30°, Δг=4,0 м, а=0.
Найти: А.
Решение. Под действием силы, приложенной к пружине, происходит движение тела и упругая деформация пружины, поэтому искомая работа

Задача сводится к нахождению силы, совершающей работу, и абсолютного удлинения х.
На брусок действует сила упругости пружины Fynp, численно равная силе F, приложенной к пружине, сила тяжести mg, сила трения FTP и сила нормальной реакции опоры Np.

Основное уравнение динамики при равномерном движении:

в проекции на оси Ох и Оу:

Учитывая, что
FTP = μNp
из этих уравнений находим силу:
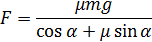
По закону Гука
F=kx
Поэтому

Подставляя значения F их, получаем

Задача 7
Какую минимальную работу надо совершить, чтобы однородный куб, находящийся на горизонтальной плоскости, перевернуть с одной грани на соседнюю? Масса куба 100 кг, длина его ребра 50 см.
Дано: m = 100 кг, а = 0,50 м.
Найти: А.
Решение. Будем переворачивать куб так, чтобы он не отрывался от горизонтальной плоскости и не скользил по ней. Центр тяжести куба перемещается при этом с высоты h1 до высоты h2.

Совершаемая работа — это работа против сил тяжести куба
Из рисунка видно, что

Следовательно,

Задача 8
Автомобиль массой 2000 кг трогается с места и движется в гору, уклон которой равен 0,020. Пройдя расстояние 100 м, он развивает скорость 32,4 км/ч. Коэффициент трения 0,050. Определите среднюю мощность, развиваемую мотором автомобиля при этом движении.
Дано: m = 2000 кг, sinα = 0,020, Δг= 100 м. v = 9,0м/с,μ = 0,050, v0 = 0.
Найти: <N>.
Решение. Искомая мощность
<N> = F<v>,
где F — сила тяги автомобиля.
Средняя скорость движения автомобиля:

Запишем основное уравнение динамики


В проекции на оси Ох и Оу:


Учитывая, что
FTp = μNp
из этих уравнений найдем
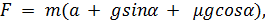
где

Ускорение при равноускоренном движении

следовательно,

Задача 9.
Определите мощность двигателя, приводящего в движение транспортер, который за сутки поднимает 2,0 • 106 т железной руды с поверхности Земли на высоту 5,0 м, если КПД транспортера равен 63 %.
Дано: t= 86400 с, m = 2,0 • 109 кг, h = 5,0 м, η = 0,63.
Найти: N.
Решение. По определению

где N — затраченная мощность,
Nn — полезная мощность, т.е. мощность, потребляемая непосредственно для поднятия груза:

где A = mgh — работа, совершенная против силы тяжести груза.
Следовательно,

Задача 10.
Тело брошено вертикально вверх со скоростью 16 м/с. На какой высоте кинетическая энергия тела равна его потенциальной энергии? Сопротивлением воздуха пренебречь.
Дано: v0 =16м/с, Wk=Wn
Найти: h.
Решение. Система "тело—Земля" является замкнутой.

Следовательно, полная механическая энергия сохраняется. За нулевой уровень потенциальной энергии принимаем уровень, с которого было брошено тело.
В состоянии 1 полная механическая энергия

в состоянии 2 она составляет

По закону сохранения энергии

По условию

Следовательно,

Задача 11.
Человек стоит на неподвижной тележке и бросает горизонтально камень массой 8 кг со скоростью 5 м/с. Определите, какую работу совершает человек, если его масса вместе с тележкой 160 кг.
Дано. m1=8 кг, v1=5 м/с, m2=160кг
Найти: А.
Решение. Работа, совершенная человеком в момент броска, равна изменению механической энергии системы «человек с тележкой – камень»
A=ΔW
Так как камень и человек в момент, непосредственно предшествующий броску, покоились, то

Где  - скорость тележки с человеком в момент непосредственно после броска
- скорость тележки с человеком в момент непосредственно после броска
По закону сохранения импульса

Следовательно,

Задача 12
Цирковой артист массой 60 кг прыгает с высоты 10 м на растянутую сетку. С какой средней силой он давит на сетку, если она прогибается на 1,0 м?
Дано: m = 60 кг, h = 10 м, х = 1,0 м.
Найти: <F>
Решение. Система "артист—Земля—сетка" является замкнутой. Следовательно, выполняется закон сохранения энергии.
Полная механическая энергия системы в состоянии 1 составляет

в состоянии 2


На основании закона сохранения энергии

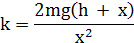
Так как по закону Гука сила упругости пропорциональна величинедеформации, то

По третьему закону Ньютона искомая сила<F> = <Fynp>. Следовательно,

Задача 13
Камень массой 50 г, брошенный под углом к горизонту с высоты20 м над поверхностью Земли со скоростью 18 м/с, упал на Землю со скоростью 24 м/с. Найдите работу по преодолению сил сопротивления воздуха.
Дано: m = 0,050 кг, h = 20 м, v0= 18м/с, v = 24 м/с
Найти: А.
Решение. Система "камень—Земля" — замкнутая, но между телами действует сила сопротивления воздуха. Поэтому полная механическаяэнергия не сохраняется и ΔW = Ас.

Полная механическая энергия в состоянии 1 составляет

в состоянии 2

Следовательно,

ВОПРОСЫИ ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ
1. Тело движется по окружности с постоянной по модулю скоростью. Изменяется ли его импульс?
2. От чего зависит изменение скорости тела? изменение импульса тела?
3. Одинаковое ли значение имеет в различных инерциальных системах отсчета импульс тела? изменение импульса тела?
4. Как импульс силы связан с импульсом тела?
5. Автомобиль при торможении движется замедленно. Как направлен вектор изменения его импульса?
6. Тело массой m брошено вертикально вверх со скоростью v0. Найдите изменение импульса а) за время подъема на максимальную высоту, б) за все время движения.
7. Футболист преграждает путь мячу. Когда сильнее он почувствует удар мяча: когда бежит навстречу мячу? когда бежит от мяча? когда стоит неподвижно?
8. Усилий нескольких человек достаточно, чтобы сдвинуть с места автобус. Почему этот же автобус не сдвигается с места от попадания противотанкового снаряда, пробивающего его навылет?
9. Могут ли внутренние силы изменить импульс системы тел? импульсы тел системы?
10. В каких случаях закон сохранения импульса применяют к незамкнутым системам?
11. Может ли человек, стоящий на идеально гладкой ледяной поверхности, сдвинуться с места, не упираясь острыми предметами в лед?
12. Могут ли осколки взорвавшейся гранаты лететь в одном направлении, если до взрыва граната покоилась?
13. Снаряд в верхней точке траектории полета разорвался на два осколка, один из которых упал на землю точно под местом разрыва. Определите возможные направления полета второго осколка.
14. Могут ли двигаться ракеты в безвоздушном пространстве? Какое влияние на движение ракеты оказывает воздушная среда?
15. Каким образом можно изменять движение космического корабля после выведения на орбиту?
16. Для чего используются многоступенчатые ракеты?
17. Какие два фактора обязательны для совершения механической работы?
18. Совершает ли неподвижно стоящий человек механическую работу, удерживая камень на вытянутой руке?
19. Совершается ли механическая работа, если на движущееся тело действуют взаимно уравновешивающиеся силы?
20. При каких условиях работа данной силы, действующей на движущееся тело, максимальна? равна нулю? отрицательна?
21. Зависит ли работа от выбора системы отсчета?
22. Как рассчитать работу переменной силы?
23. Как зависит мощность силы от скорости движения?
24. Человек опускается на парашюте. Какая сила совершает при этом положительную и какая отрицательную работу?
25. Совершает ли работу сила притяжения Луны Землей?
26. Если автомобиль въезжает на гору при неизменной мощности двигателя, то водитель уменьшает скорость движения. Почему?
27. От чего зависит работа силы тяжести?
28. Чему равна работа силы тяжести при горизонтальном движении тела? при движении тела по замкнутой траектории?
29. Тело свободно падает с некоторой высоты. Одинаковую ли работу совершает сила тяжести за одинаковые промежутки времени?
30. Зависит ли работа силы упругости от формы траектории?
31. В чем сходство работ, совершаемых силой упругости и силой тяжести?
32. Две одинаковые пружины (железная и медная) упруго растянуты а) на одинаковую длину, б) одинаковыми силами. На растяжение которой из них надо затратить большую работу в случаях а) и б)?
33. Всегда ли работа силы трения скольжения отрицательна?
34. Может ли быть работа силы трения скольжения равной нулю?
35. Может ли совершать работу сила трения покоя?
36. Тело массой m поднимают на высоту h a) вертикально вверх, б) по гладкой наклонной плоскости, в) по шероховатой наклонной плоскости. Сравните работы внешней силы и силы тяжести.
37. В чем отличие консервативных сил от неконсервативных?
38. В каких случаях импульс тела изменяется, а кинетическая энергия остается неизменной?
39. Как изменяется кинетическая энергия тела, если приложенная сила совершает положительную (отрицательную) работу?
40. Какая энергия является мерой взаимодействия тел?
41. Может ли потенциальная энергия быть отрицательной?
42. Почему уровень начала отсчета потенциальной энергии в разных задачах можно выбирать произвольно?
43. От чего зависит потенциальная энергия тела, поднятого над Землей? Как изменяется она при движении тела вверх? вниз? Как связана она с работой силы тяжести?
44. От чего зависит потенциальная энергия упруго деформированного тела? Как связана она с работой силы упругости?
45. Как изменяется потенциальная энергия пружины при ее растяжении? при сжатии?
46. Какой энергией обладает тело, поднятое над Землей? свободно падающее тело?
47. Что понимают под полной механической энергией? Всегда ли в замкнутой системе полная механическая энергия сохраняется?
48. Тело брошено вертикально вверх. Изменяется ли полная механическая энергия? Какие взаимные превращения механической энергии происходят при движении тела, если сила сопротивления не действует?
49. Тело свободно падает с высоты h над поверхностью Земли. Постройте графики зависимости его потенциальной, кинетической и полной энергии в зависимости от высоты тела над Землей
50. Тело соскальзывает без трения с клина, лежащего на горизонтальной плоскости, два раза: первый раз клин закреплен, второй раз клин может скользить без трения. Будет ли скорость тела в конце клина одинаковой в обоих случаях, если тело оба раза соскальзывало с одной и той же высоты?
51. Движущийся вагон сталкивается с пружинным амортизатором. Во что превращается его кинетическая энергия?
52. Как изменяется полная механическая энергия замкнутой системы тел, если тела взаимодействуют между собой силами трения?
53. Человек спускается на парашюте. Как изменяется его кинетическая энергия? потенциальная? полная механическая энергия?
54. Чем отличается абсолютно неупругий удар от абсолютно упругого? Как изменяется кинетическая и потенциальная энергии тел в процессе соударения? Сохраняется ли при этом полная механическая энергия тел?
55. Какими законами сохранения можно пользоваться при рассмотрении упругого и неупругого ударов?
56. Тело массой m1 движущееся со скоростью v, упруго ударяется о покоящееся тело массой m2. От чего зависит направление движения тела массой m1 после удара? В каком случае оно отскочит назад? остановится? будет продолжать движение в том же направлении?
57. Когда покоящийся шар приобретает большую скорость от другого такого же шара: при упругом или при неупругом соударении?
58. Почему при одинаковом ударе палкой о камень и теннисный мяч последний летит дальше?
59. Хоккейная шайба массой 300 г после удара клюшкой, который длился 0,02 с, начала скользить со скоростью 20 м/с. Определите среднюю силу удара.
60. Мяч массой 0,5 кг летит горизонтально со скоростью 14 м/с. Футболист бьет по мячу и отправляет его в противоположном направлении со скоростью 20 м/с. Удар длится 0,02 с. Определите среднюю силу удара по мячу.
61. Два тела, массы которых2 кг и6 кг, движутся навстречу друг другу со скоростью 2 м/с каждое. Определите модуль и направление скорости тел после абсолютно неупругого удара.
62. Из ружья массой5 кг вылетает пуля массой 9 г со скоростью600 м/с. Найдите скорость отдачи ружья.
63. Мальчик тянет санки, прилагая к веревке силу100 Н. Веревка образует с горизонтом угол 30°. Чему равна работа силы, если санки переместились на расстояние 50 м? Какую мощность развивает мальчик, если скорость санок1м/с?
64. Акула массой250 кг плывет со скоростью 4 м/с. Чему равна ее кинетическая энергия?
65. Импульс тела8 кг • м/с, а его кинетическая энергия 16 Дж. Определите массу тела.
66. Как изменится потенциальная энергия тела, находящегося на высоте 2 м над поверхностью Земли, если увеличить высоту еще на 4 м? Потенциальную энергию тела на поверхности Земли считайте равной нулю. Масса тела5 кг.
67. Найдите жесткость пружины, если при сжатии ее на 0,05 м в пружине запасается потенциальная энергия 25 Дж.
68. С яблони высотой 5 м упало яблоко. Масса яблока 0,2 кг. Чему равна кинетическая энергия яблока в момент касания поверхности земли?
69. Тело массой 50 г, брошенное вертикально вверх с начальной скоростью 30 м/с, достигло высшей точки подъема через 2,5 с. Найдите среднюю силу сопротивления воздуха, действовавшую на тело во время полета.
70. Железнодорожная платформа (масса платформы с орудием и снарядом 20 т) движется со скоростью 9 км/ч. Из орудия, установленного на платформе, выпущен снаряд массой 25 кг в горизонтальном направлении со скоростью 700 м/с относительно земли. Определите скорость платформы после выстрела, если он произведен в направлении движения платформы.
71. Тело брошено вверх с начальной скоростью 20 м/с. На какой высоте его кинетическая энергия будет равна потенциальной? Потенциальную энергию в начальной точке считайте равной нулю.
ПРИЛОЖЕНИЕ
Тест
1. Как называется величина, равная произведению массы тела на ее скорость?
a. инертность;
b. импульс тела;
c. импульс силы;
d. перемещение.
2. Тело массой 2 кг движется со скоростью 4 м/с. Каков импульс тела?
a. 10 кг м/с
b. 8 кг м/с
c. 2 кг м/с
d. 6 кг м/с
3. Как называется физическая величина, равная произведению модулей силы и перемещения и косинуса угла между ними?
a. потенциальная энергия;
b. работа;
c. мощность;
d. кинетическая энергия.
4. Тело массой 3 кг поднято на высоту10 м. Какова потенциальная энергия тела?
a. 30 Дж
b. 300 Дж
c. 100 Дж
d. 3 Дж
5. Поставьте соответствие между физическими величинами и их обозначением:
a. масса а) Ер
b. сила б) m
c. кинетическая энергия в) А
d. мощность г) F
e. работа д) N
f. потенциальная энергия е) Ек
6. Два шара с одинаковыми массами по 50 г двигались навстречу друг другу одинаковыми по модулю скоростями 2 м/с. После неупругого столкновения шары остановились. Каково изменение суммы импульсов двух шаров в результате столкновения?
a. 100 
b. 200 
c. 0,1 
d. 1 
7. Камень брошен вертикально вверх. На пути 1м его кинетическая энергия уменьшилась на 16 Дж. Какую работу совершила сила тяжести на этом пути?
a. 16 Дж.
b. 4 Дж.
c. 0 Дж.
d. 8 Дж
8. Как называется физическая величина, равная произведению силы на время ее действия?
a. импульс тела
b. импульс силы
c. кинетическая энергия
d. работа
9. Как называется физическая величина, равная отношению работы к интервалу времени, за который эта работа совершена?
a. потенциальная энергия;
b. работа;
c. мощность;
d. кинетическая энергия.
10. Тело массой 3 кг движется со скоростью 10 м/с. Какова кинетическая энергия тела в данный момент движения?
a. 30 Дж
b. 150 Дж
c. 15 Дж
d. 3 Дж
11. Поставьте соответствие между физическими величинами и единицами их измерения:
a. масса а) Дж
b. сила б) Н
c. кинетическая энергия в) Вт
d. мощность г) кг
e. работа д) м/с
f. потенциальная энергия е) В
12. Два шара с одинаковыми массами по 50 г двигались навстречу друг другу одинаковыми по модулю скоростями 2 м/с. После упругого столкновения каждый шар стал двигаться в обратном направлении с прежней по модулю скоростью. Каково изменение суммы импульсов двух шаров в результате столкновения?
a. 100 
b. 200 
c. 0,1 
d. 1 
13. Тело брошено вертикально вверх со скоростью 30м/с. Если принять потенциальную энергию тела в точке бросания равной нулю, то кинетическая энергия тела будет равна половине его потенциальной энергии при подъёме на высоту?
a. 50м
b. 30м
c. 20м
d. 10м.
14. Чтобы лежащий на полу однородный стержень длины 1м и массы 10кг поставить вертикально, нужно совершить наименьшую работу, равную:
a. 100 Дж
b. 50 Дж
c. 25 Дж
d. 20 Дж.
15. Тело свободно падает с высоты 5м. Во сколько раз кинетическая энергия тела больше его потенциальной энергии в точке, находящейся на расстоянии 2м от поверхности земли?
a. 1,5
b. 1,7
c. 2
d. 2,5