МЕЖДУНАРОДНАЯ АКАДЕМИЯ БИЗНЕСА
ДЕПАРТАМЕНТ
«МАГИСТРАТУРА ДЕЛОВОГО АДМИНИСТРИРОВАНИЯ»
МУРСАЛИМОВА Т.М.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО РЕШЕНИЮ ЗАДАЧ
И
ВАРИАНТЫ
ИНДИВИДУАЛЬНОГО ДОМАШНЕГО ЗАДАНИЯ
ПО КУРСУ
«СТАТИСТИКА»
Г. АЛМАТЫ
МЕЖДУНАРОДНАЯ АКАДЕМИЯ БИЗНЕСА
ДЕПАРТАМЕНТ
«МАГИСТРАТУРА ДЕЛОВОГО АДМИНИСТРИРОВАНИЯ»
МУРСАЛИМОВА Т.М.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО РЕШЕНИЮ ЗАДАЧ
И
ВАРИАНТЫ
ИНДИВИДУАЛЬНОГО ДОМАШНЕГО ЗАДАНИЯ
ПО КУРСУ
«СТАТИСТИКА»
Г. АЛМАТЫ
ББК 60.6 (5Каз)
М 91
Мурсалимова Т.М. – кандидат экономических наук, доцент
Мурсалимова Т.М.
М 91 Методические указания по решению задач и варианты
индивидуального домашнего задания по курсу «Статистика" –Алматы: ЧП Мертенов,2007.-162 с.
ISBN 9965-448-72-8
Учебное пособие подготовлено в виде практикума, включающего методические указания по решению типовых задач по основным разделам курса «Статистика»: метод группировки; метод обобщающих показателей, включающий абсолютные, относительные, средние величины и показатели вариации; метод выборочного наблюдения; метод динамических рядов; индексный метод; корреляционно-регрессионный анализ.
Кроме этого, предложены варианты заданий для самостоятельного решения.
Для слушателей МВА и студентов экономических специальностей.
ISBN 9965-448-72-8 ББК 60.6 (5Каз)
М 91
@ Мурсалимова Т.М.,2007
Содержание
Стр.
Предисловие 4
2) Методические указания по решению задач по курсу «Статистика» 6
3) Метод группировки 7
4) Средние величины 10
5) Показатели вариации. Выборочное наблюдение 12
6) Ряды динамики 15
7) Индексы 20
8) Корреляционно-регрессионный анализ 25
Варианты индивидуального домашнего задания 30
Предисловие
Методические указания предназначены для слушателей МВА, изучающих курс «Статистика». Цель данной работы – продемонстрировать методику решения типовых задач по основным разделам курса: метод группировки (задача №1), средние величины (задача №2), показатели вариации и выборочное наблюдение (задача №3), ряды динамики (задачи №4, №5), индексы (задачи №6, №7, №8), корреляционно-регрессионный анализ (задача №9).
В задаче №1 производится группировка единиц совокупности на группы с равными интервалами. Рассчитываются обобщающие итоговые и средние показатели по группам и в целом по совокупности. Строится аналитическая групповая таблица с заданным набором показателей. Выявляется взаимосвязь между факторным и результативным признаками.
Задача №2 вырабатывает навыки расчета средних величин по формулам средней арифметической и средней гармонической.
В задаче №3 комплексно рассчитываются показатели средней, дисперсии по способу «моментов» и коэффициент вариации в выборочной совокупности, а затем с определенной долей вероятности – пределы, в которых ожидаются генеральная средняя и генеральная доля, т.е. среднее значение варьирующего признака и доля единиц, обладающих определенными характеристиками, во всей генеральной совокупности.
Задача №4 дает возможность научиться: рассчитывать абсолютные и относительные показатели динамики базисным и цепным способами (абсолютный прирост, коэффициент роста, коэффициент прироста, темп роста, темп прироста, абсолютное значение 1% прироста), средний уровень ряда динамики, среднегодовые темпы роста и прироста; строить данные ряда динамики графически; делать выводы.
В задаче №5 на примере моментного ряда динамики производится расчет средних показателей по группам и в целом по всей совокупности единиц по формуле средней хронологической.
Задача №6 имеет дело с расчетом: индивидуальных индексов цен каждой из трех различных товарных групп и общего индекса цен в среднем по трем товарным группам. Рассчитываются индекс товарооборота; индекс физического объема товарооборота; сумма экономии (или дополнительного расхода), полученная населением от изменения цен при покупке товаров в отчетном периоде по сравнению с базисным периодом.
В задаче №7 по трем товарным группам рассчитываются индивидуальные индексы и общий индекс физического объема товарооборота.
Задача №8 состоит из двух заданий: в первом – рассчитываются агрегатные индексы затрат, себестоимости и физического объема всей продукции по заводу №1; во втором – для заводов №1 и №2 по одинаковому изделию рассчитываются индексы среднего уровня себестоимости единицы продукции переменного, фиксированного составов и структурных сдвигов.
В задаче №9 производится расчет параметров линейного уравнения связи и линейного коэффициента корреляции. Делается вывод о тесноте и направлении связи между факторным и результативным признаками.
Методические указания дополняются вариантом индивидуального домашнего задания, состоящего из соответствующих задач, для самостоятельного их выполнения слушателями в процессе изучения данного курса.
Методические указания по решению задач
По курсу «Статистика»
МЕТОД ГРУППИРОВКИ
Задача 1.
Из отчетов 25 заводов получены следующие данные
| Номер завода | Стоимость основных производственных фондов, млн тг. | Выпуск продукции, млн тг. |
| 7,5 | 12,4 | |
| 8,4 | 12,5 | |
| 5,7 | 10,1 | |
| 8,6 | 14,3 | |
| 6,6 | 12,9 | |
| 3,4 | 3,5 | |
| 1,9 | 2,5 | |
| 3,7 | 4,9 | |
| 3,8 | 2,7 | |
| 1,2 | 2,3 | |
| 8,6 | 18,3 | |
| 9,3 | 19,6 | |
| 5,9 | 9,7 | |
| 5,1 | 10,4 | |
| 5,2 | 10,3 | |
| 8,6 | 20,6 | |
| 4,7 | 6,0 | |
| 3,8 | 3,6 | |
| 10,2 | 18,0 | |
| 6,3 | 9,7 | |
| 6,3 | 10,6 | |
| 2,5 | 3,6 | |
| 4,1 | 4,6 | |
| 7,6 | 12,4 | |
| 5,7 | 6,8 |
С целью выявления зависимости между стоимостью основных производственных фондов (ОПФ) и выпуском продукции, произвести группировку заводов по стоимости ОПФ, образовав 5 групп заводов с равными интервалами.
Каждую группу охарактеризуйте:
1) числом заводов;
2) размером ОПФ:
· всего по группе,
· в среднем на 1 завод;
3) выпуском продукции:
· всего по группе,
· в среднем на один завод;
4) размером валовой продукции на 1 тг. стоимости ОПФ (показатель фондоотдачи).
Результаты представьте в виде групповой таблицы. Сделайте
выводы.
Решение:
По условию задачи необходимо образовать 5 групп заводов (n=5) с равными интервалами ( ):
):  .
.
 Найдем хmax и хmin из второй графы исходной таблицы (по стоимости ОПФ):
Найдем хmax и хmin из второй графы исходной таблицы (по стоимости ОПФ):
хmax=10,2; хmin=1,2;
 =
=  млн тг.
млн тг.
Рабочая таблица №1.
| № группы | Группы заводов по стоимости ОПФ, млн тг. | Число заводов |
| 1,2 – 3,0 | ||
| 3,0 – 4,8 | ||
| 4,8 – 6,6 | ||
| 6,6 – 8,4 | ||
| 8,4 – 10,2 | ||
| Итого: | - |
Рабочая таблица №2.
| Группы заводов по стоимости ОПФ, млн тг. | № завода | Стоимость ОПФ, млн тг. | Выпуск продукции, млн тг. |
| А | |||
| 1) 1,2-3,0 | 1,2 1,9 2,5 | 2,3 2,5 3,6 | |
| Всего по группе В среднем на 1 завод | 5,6 1,9 | 8,4 2,8 |
(продолжение)
| А | |||
| 2)3,0 – 4,8 | 3,4 3,7 3,8 4,7 3,8 4,1 | 3,5 4,9 2,7 6,0 3,6 4,6 | |
| Всего по группе В среднем на 1 завод | 23,5 3,9 | 25,3 4,2 | |
| 3)4,8 – 6,6 | 5,7 5,9 5,1 5,2 6,3 6,3 5,7 | 10,1 9,7 10,4 10,3 9,7 10,6 6,8 | |
| Всего по группе В среднем на 1 завод | 40,2 5,7 | 67,6 9,7 | |
| 4)6,6 – 8,4 | 6,6 7,5 7,6 | 12,9 12,4 12,4 | |
| Всего по группе В среднем на один завод | 21,7 7,2 | 37,7 12,6 | |
| 5)8,4-10,2 | 8,4 8,6 8,6 9,3 8,6 10,2 | 12,5 14,3 18,3 19,6 20,6 18,0 | |
| Всего по группе В среднем на один завод | 53,7 9,0 | 103,3 17,2 |
Групповая таблица
Группировка заводов по стоимости ОПФ
| Группы заводов по стоимости ОПФ, млн тг. | Число заводов | Стоимость ОПФ, млн тг. | Выпуск продукции, млн тг. | Стоимоcть валовой продукции на 1тг. стоимости ОПФ | ||
| всего по группе | в среднем на 1 завод | всего по группе | в среднем на 1завод | |||
| А | 6 = 4:2 |
(продолжение)
| А | ||||||
| 1,2-3,0 3,0-4,8 4,8-6,6 6,6-8,4 8,4-10,2 | 5,6 23,5 40,2 21,7 53,7 | 1,9 3,9 5,7 7,2 9,0 | 8,4 25,3 67,6 37,7 103,3 | 2,8 4,2 9,7 12,6 17,2 | 1,5 1,1 1,7 1,7 1,9 | |
| Итого: | 144,7 | 5,8 | 242,3 | 9,7 | 1,7 |
Получили аналитическую таблицу зависимости стоимости выпуска продукции от стоимости ОПФ: с ростом стоимости ОПФ в среднем на 1 завод прямо пропорционально возрастает стоимость выпущенной продукции в среднем на один завод.
Фондоотдача – это обобщающий показатель использования ОПФ. Он показывает сколько продукции (в стоимостном выражении) произведено в данном периоде на 1 тг. стоимости ОПФ. Чем лучше используются ОПФ, тем выше показатель фондоотдачи.
СРЕДНИЕ ВЕЛИЧИНЫ
Задача 2.
По данным отчетов трех фабрик фактический выпуск готовой продукции в отчетном периоде составил, соответственно, 460, 240 и 310 тыс. тг.
План выпуска готовой продукции первой фабрикой был выполнен на 105%, второй – на 100%, третьей – на 95%. Процентная доля продукции 1 сорта в общем объеме выпущенной продукции за тот же период времени составила на трех фабриках, соответственно, 86, 90 и 92.
Определить:
1) средний процент выполнения плана выпуска готовой продукции по трем фабрикам вместе;
2) средний процент продукции 1 сорта по трем фабрикам вместе.
Укажите, какие виды средних нужно применять для вычисления этих показателей.
Решение:
Запишем исходные данные задачи в таблицу:
| Фабрика | Фактический выпуск продукции, тыс.тг. | % выполнения плана | % продукции 1 сорта |
| Итого: | - | - |
1) Средний % Фактический выпуск продукции на
выполнения трех фабриках вместе × 100%
 плана по трем = Плановый выпуск продукции на
плана по трем = Плановый выпуск продукции на
фабрикам вместе трех фабриках вместе
Из условия задачи плановый выпуск продукции на каждой из фабрик неизвестен. Его можно найти по формуле:
Плановый Фактический выпуск продукции. 100%

 выпуск = % выполнения плана.
выпуск = % выполнения плана.
продукции
Плановый выпуск продукции 460 × 100 240 × 100 310 ×100




 = + + по трем фабрикам вместе 105 100 95
= + + по трем фабрикам вместе 105 100 95
Cредний % выполнения плана 460+240+310
 = ×100 =
= ×100 =
по трем фабрикам вместе 460 × 100 + 240×100 + 310 ×100




105 100 95
 = = 100,6 %.
= = 100,6 %.
10,04
Для вычисления среднего % выполнения плана по трем фабрикам вместе использовали формулу средней гармонической; 
 ,
,
где wi – фактический выпуск продукции на каждой фабрике;
хi – % выполнения плана на каждой фабрике.
Количество изделий 1 сорта на
2)Средний % продукции трех фабриках вместе × 100%
 1 сорта по трем = Фактический выпуск продукции.
1 сорта по трем = Фактический выпуск продукции.
фабрикам вместе на трех фабриках вместе
Из условия задачи количество изделий 1 сорта на каждой из фабрик неизвестно. Его можно найти по формуле:
(%продукции ´ (фактический
 Количество 1 сорта) выпуск продукции)
Количество 1 сорта) выпуск продукции)
 изделий 1 сорта =.
изделий 1 сорта =.

 Количество 86 × 460 90 × 240 92 ×310
Количество 86 × 460 90 × 240 92 ×310


 изделий 1 сорта = + +.
изделий 1 сорта = + +.
на трех фабриках вместе 100 100 100,


 86 × 460 + 90 × 240 + 92 × 310
86 × 460 + 90 × 240 + 92 × 310
Средний % продукции 100 100 100
 1 сорта по = × 100 =
1 сорта по = × 100 =
трем фабрикам вместе 460+ 240 + 310

Для вычисления среднего процента продукции 1 сорта по трем фабрикам вместе использовали формулу средней арифметической:

 ,
,
где хi - % продукции 1 сорта на каждой фабрике;

 - фактический выпуск продукции на каждой фабрике.
- фактический выпуск продукции на каждой фабрике.
ПОКАЗАТЕЛИ ВАРИАЦИИ.
ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Задача 3.
Для изучения норм выработки на заводе было проведено 20%-ое выборочное обследование рабочих. В выборку попало 400 рабочих, показавших следующие затраты времени на 1 деталь:
| Затраты времени на 1 деталь, мин. | Число рабочих ¦ | х | (А=19) х-А | 

|
 ¦ ¦
|

|
 × ¦ × ¦
|
| До 14 | - 6 | - 3 | - 15 | ||||
| 14-16 | - 4 | - 2 | - 70 | ||||
| 16-18 | - 2 | - 1 | - 100 | ||||
| 18-20 | |||||||
| 20-22 | |||||||
| 22-24 | |||||||
| Свыше 24 | |||||||
| Итого: | - | - | - | - 69 | - |
Вычислить:
1)  применяя способ «моментов» или простой способ,
применяя способ «моментов» или простой способ,
а) средние затраты времени на 1 деталь;
б) среднее квадратическое отклонение (s);
2) коэффициент вариации (n);
3) с вероятностью 0,954 предельную ошибку выборки и пределы, в которых ожидается среднее время обработки одной детали рабочими завода;
4) с вероятностью 0,954 пределы, в которых ожидается доля рабочих, затрачивающих на обработку 1 детали свыше 20 минут.
Решение:
1a) Средние затраты времени на обработку 1 детали по способу «моментов» рассчитываются по формуле:
 , где
, где
 – момент 1-го порядка;
– момент 1-го порядка;
 ;
; 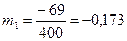 ;
;
 = 2 – величина интервала;
= 2 – величина интервала;
А = 19 -условный ноль.

 = 2 (- 0,173) + 19 = - 0,346 + 19 = 18,654 мин.
= 2 (- 0,173) + 19 = - 0,346 + 19 = 18,654 мин.
1б) Среднее квадратическое отклонение по способу «моментов» рассчитывается по формуле:
 , где
, где
 - момент 2 го порядка;
- момент 2 го порядка; 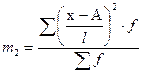 ;
;  .
.
Дисперсия s2 = 22[1,223-(-0,173)2 ] = 4×1,193 = 4,772.
 Среднее квадратическое отклонение
Среднее квадратическое отклонение  мин.
мин.
2) Коэффициент вариации n рассчитывается по формуле:
 ;
;  %.
%.
Так как n £ 33 %, то исследуемое множество показателей времени обработки 1 детали во всей выборочной совокупности рабочих является однородным, а полученные средние затраты времени на обработку одной детали являются показателем, типичным для данной совокупности.
 |
3) По условию задачи выборочная совокупность рабочих составила 400 человек (n=400). Эта совокупность была получена путем 20%-го выборочного обследования. Следовательно, генеральная совокупность (общее количество рабочих на данном заводе) N= 2000 человек:
400 – 20%
N - 100%
 (чел.).
(чел.). 
Фрагмент таблицы взаимосвязи показателей вероятности Р и коэффициента доверия t имеет вид:
| P | 0,683 | 0,954 | 0,997 | 0,999 |
| t |
По условию задачи Р=0,954, значит t=2. В п. 1а были найдены средние затраты времени на обработку 1 детали в выборочной совокупности рабочих (n=400).
Обозначим их  . Найдем предельную ошибку
. Найдем предельную ошибку  , которая ожидается при заданных условиях задачи.
, которая ожидается при заданных условиях задачи.


 , где
, где 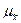 =
= 
 - средняя ошибка выборочной средней.
- средняя ошибка выборочной средней.
При расчете показателя 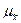 применили формулу для бесповторного отбора, что следует из условия задачи, тогда
применили формулу для бесповторного отбора, что следует из условия задачи, тогда
 мин.
мин.
Найдем пределы, в которых ожидается среднее время обработки одной детали рабочими завода ( ).
).



Таким образом, с вероятностью Р = 0,954 можно утверждать, что в 954 случаях из 1000 среднее время обработки одной детали рабочими завода (генеральная средняя) заключено в вышеуказанном интервале [18,459 мин.; 18,849 мин.].
 4)По условию задачи имеем исходные данные:
4)По условию задачи имеем исходные данные:
N= 2000чел.;
n= 400 чел.;
Р= 0,954;
t= 2;
m= 52+20+8 = 80 чел. – число рабочих, затрачивающих на. обработку 1 детали свыше 20 минут;
 - доля рабочих, затрачивающих на. обработку 1 детали свыше 20 минут.
- доля рабочих, затрачивающих на. обработку 1 детали свыше 20 минут.
Предельная ошибка выборочной доли Dw рассчитывается по формуле бесповторного отбора:
Dw= t×mw= t× 

 .
.
Пределы, в которых ожидается доля рабочих завода(генеральная доля), затрачивающих на обработку 1 детали свыше 20 минут, рассчитываются из двойного неравенства:
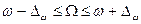


 .
.
Таким образом, с вероятностью Р=0,954 можно утверждать, что в 954 случаях из 1000 доля рабочих завода, затрачивающих на обработку 1 детали свыше 20 минут, находится в пределах [16,4 %; 23,6%].
РЯДЫДИНАМИКИ
Задача 4.
Производство маргариновой продукции в РК характеризуется следующими данными:
| Год | Производство маргариновой продукции, тыс. т (у) |
| 71,4 | |
| 47,7 | |
| 35,1 | |
| 18,3 |
Вычислить: абсолютные и относительные показатели динамики:
1) базисным и цепным способом:
· абсолютный прирост (Dу);
· коэффициент роста (К);
· коэффициент прироста ( К);
К);
· темп роста (Т);
· темп прироста ( Т);
Т);
2) абсолютное значение 1% прироста;
3) средний уровень ряда ( );
);
4) среднегодовые темпы роста и прироста 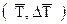 .
.
Изобразить данные ряда графически.
Сделать выводы.
Решение:
Абсолютные и относительные показатели динамика из пп.1-2 рассчитаем по формулам и поместим в таблицу:
Dyбаз. = уi- y0 Т баз. = К баз ×100%
Dу цепн. = yi –у i-1  Т цепн.= К цепн. ·100%
Т цепн.= К цепн. ·100%

 Тбаз. = Тбаз. – 100%
Тбаз. = Тбаз. – 100%
 DТ цепн. = Т цепн. – 100%
DТ цепн. = Т цепн. – 100%
DКбаз. = К баз. – 1 

DК цепн. = К цепн. – 1
пп.1-2)
| Год | Производство маргариновой продукции, тыс. т (у) | Абсолютный прирост, тыс. т | Коэффициент роста | Коэффициент прироста | Темп роста, % | Темп прироста, % | Абс. значе ние 1% прироста, тыс. т (А) | |||||
| Dубаз. | Dуцепн | Кбаз. | Кцепн | DКбаз. | DКцепн | Тбаз. | Тцепн | DТбаз. | DТцепн | |||
| 71,4 | … | 1,000 | … | … | 100,0 | … | … | … | ||||
| 47,7 | -23,7 | -23,7 | 0,668 | 0,668 | -0,332 | -0,332 | 66,8 | 66,8 | -33,2 | -33,2 | 0,714 | |
| 35,1 | -36,3 | -12,6 | 0,492 | 0,736 | -0,508 | -0,264 | 49,2 | 73,6 | -50,8 | -26,4 | 0,477 | |
| 18,3 | -53,1 | -16,8 | 0,256 | 0,521 | -0,744 | -0,479 | 25,6 | 52,1 | -74,4 | -47,9 | 0,351 |
3) Найдем средний уровень ряда  .
.
Так как имеем интервальный ряд динамики, то средний уровень рассчитаем по формуле:
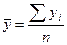 .
.
 тыс.т,
тыс.т,
т.е. в среднем в рассматриваемом периоде 1990-1993 гг. ежегодно производили в РК 43,125 тыс. т маргариновой продукции.
4) Среднегодовой темп роста производства маргариновой продукции рассчитывается по формуле:
 =
=  ×100%,
×100%,
где  - среднегодовой коэффициент роста производства маргариновой
- среднегодовой коэффициент роста производства маргариновой
продукции может быть рассчитан двумя способами:
· базисным способом:
 , где n –число уровней ряда, включая
, где n –число уровней ряда, включая
базисный; n=4.
 ;
;
· цепным способом:
 , где
, где  - цепные коэффициенты роста;
- цепные коэффициенты роста;
 m – число цепных
m – число цепных
коэффициентов роста; m=3.
 .
.
Тогда  = 0,635× 100%= 63,5%.
= 0,635× 100%= 63,5%.
Среднегодовой темп прироста рассчитывается по формуле:

Таким образом, ежегодный рост производства маргариновой продукции в РК за период 1990 – 1993 гг. в среднем составил 63,5%, т.е. в среднем ежегодно производство маргариновой продукции в РК уменьшалось на 36,5%.
Динамику производства маргариновой продукции в РК за 1990-1993 гг. можно проследить графически при помощи линейной и столбиковой диаграмм.
Линейная диаграмма

Динамика производства маргариновой продукции
в РК за 1990 – 1993 гг. (в процентах к 1990 г.)
Столбиковая диаграмма

Динамика производства маргариновой продукции
в РК за 1990-1993 гг. (тыс.тонн)
Вывод: В среднем за рассматриваемый период 1990-1993гг. ежегодно
производили в РК 43,125 тыс. тонн маргариновой продукции.
Причем ее производство за эти годы резко уменьшалось.
Среднегодовой темп роста производства составил всего лишь
63,5%, т.е. в среднем ежегодно производство этой
продукции сокращалось на 36,5%.
Задача 5.
Товарные остатки по двум группам товаров на 1-ое число каждого месяца составили:
 (тыс.тг.)
(тыс.тг.)
| Товарная группа | Дата | ||||
| 1 января | 1февраля | 1марта | 1апреля | ||
| 1.Прoдовольст венные товары | |||||
| 2.Непродовольст венные товары | |||||
| Всего: | |||||

Вычислить средний квартальный остаток:
1) по продовольственным товарам;
2) по непродовольственным товарам;
3) по обеим группам вместе.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4 и 5 различны.
Решение:
В задаче 4 имеем интервальный ряд, а в задаче 5 – моментный ряд. Для моментного ряда средняя определяется по формуле средней хронологической:
 ,
,
где n- число уровней ряда.
По условию задачи n = 4, т.е. данный моментный ряд имеет четыре уровня.
1) Средний квартальный остаток по продовольственным товарам равен:
 тыс.тг.
тыс.тг.
2) Средний квартальный остаток по непродовольственным товарам равен:
 тыс. тг.
тыс. тг.
3) Средний квартальный остаток по обеим группам вместе равен:
 тыс. тг.
тыс. тг.
ИНДЕКСЫ
Задача 6.
Имеются следующие данные о товарообороте магазина:
| Товарная группа | Продано товаров в фактических ценах, тыс. тг. | Процент изменения цен во 2 квартале по сравнению с 1 кварталом | |
| 1 квартал (p0q 0) | 2 квартал (p1q1) | ||
| + 15 | |||
| -6 | |||
| без изменения | |||
| Итого: | - |
Вычислить:
1) индивидуальные и общий индексы цен;
2) общий индекс товарооборота в фактических ценах;
3) используя взаимосвязь индексов товарооборота и цен, вычислить общий индекс физического объема товарооборота;
4) сумму экономии или дополнительного расхода от изменения цен, полученную населением при покупке товаров в данном магазине.
Сделайте выводы.
Решение:
1) Вычислим индивидуальные индексы цен (ip):
по 1 группе товаров ip = 100% + 15% = 115%, или 1,15;
по 2 группе товаров ip = 100% - 6% = 94 %, или 0,94;
по 3 группе товаров ip = 100%, или 1,00.
Исходя из имеющихся данных, общий индекс цен (Ip) рассчитывается, как среднегармонический индекс цен:
 , тогда
, тогда
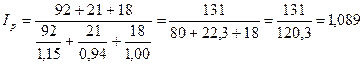 .
.
Это значит, что в среднем цены в магазине во 2 квартале выросли по сравнению с 1 кварталом на 8,9%.
2) Вычислим общий индекс товарооборота  в данном магазине по формуле:
в данном магазине по формуле:
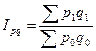 ; тогда
; тогда  ,
,
т.е. товарооборот магазина вырос во 2 квартале по сравнению с 1 кварталом на 32,3%.
3) Взаимосвязь индексов товарооборота, цен и физического объема товарооборота имеет вид:
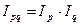 , отсюда
, отсюда  .
.