Задача 9.
Товарооборот и издержки обращения в 10 магазинах города за отчетный период характеризуются следующими данными:
| Номер магазина | Товаро оборот, млн тг. (х) | Издержки обращения,млн тг. (у) |
| 0,2 | ||
| 0,5 | ||
| 0,6 | ||
| 0,6 | ||
| 0,8 | ||
| 0.7 | ||
| 0,9 | ||
| 0,7 | ||
| 0,9 | ||
| 0,2 | ||
| Итого: | 6,1 |
1. Для изучения зависимости между объемом товарооборота и издержками обращения построить линейное уравнение связи.
2. Для определения тесноты связи вычислить линейный коэффициент корреляции.
Поясните смысл полученных показателей.
Решение:
1. Зависимость между издержками обращения и объемом товарооборота определим линейным уравнением связи
(уравнением регрессии): у = а0 + а1х,
где у – издержки обращения (результативный признак);
х – объем товарооборота (факторный признак);
а0,а1 – параметры уравнения регрессии.
Параметры а0, а1 можно определить из системы нормальных уравнений, полученных по методу наименьших квадратов:

или по формулам:
 ;
;
 .
.
Для расчета параметров а0,а1 воспользуемся данными таблицы:
| Номер магазина | Товаро оборот, млн тг. (х) | Издержки обраще- ния, млн тг. (у) | ху | х2 | у2 | ух |
| 0,2 | 1,2 | 0,04 | 0,345 | |||
| 0,5 | 2,5 | 0,25 | 0,319 | |||
| 0,6 | 10,2 | 0,36 | 0,631 | |||
| 0,6 | 11,4 | 0,36 | 0,683 | |||
| 0,8 | 19,2 | 0,64 | 0,813 | |||
| 0,7 | 9,1 | 0,49 | 0,527 | |||
| 0,9 | 23,4 | 0,81 | 0,865 | |||
| 0,7 | 13,3 | 0,49 | 0,683 | |||
| 0,9 | 25,2 | 0,81 | 0,917 | |||
| 0,2 | 1,0 | 0,04 | 0,319 | |||
| Итого: | 6,1 | 116,5 | 4,29 | 6,102 |
Для данной задачи система нормальных уравнений имеет вид:

Решив систему, найдем параметры а0, а1: а0 = 0,189,
а1 = 0,026.
Параметр а1 называется коэффициентом регрессии. Он показывает на сколько единиц изменяется результативный признак при изменении факторного признака на 1. В задаче а1 = 0,026 млн тг., значит при увеличении товарооборота на 1 млн тг. издержки обращения увеличиваются на 0,026 млн тг.
Линейное уравнение связи (уравнение регрессии) имеет вид:
| ух = 0,189 + 0,026х |
где ух - точки теоретической линии регрессии (графа 7), расчет которых производится подстановкой соответствующих значений х в полученное уравнение регрессии.
Если математическое уравнение связи подобрано правильно, то  или очень близки. Так как
или очень близки. Так как  ;
;  , уравнение регрессии построено правильно.
, уравнение регрессии построено правильно.
2. При линейной зависимости между признаками для определения
тесноты и направления связи вычислим линейный коэффициент корреляции по формуле:
 ,
,
где  ,
,  ,
,  - средние значения признаков;
- средние значения признаков;
 - средние квадратические отклонения по х и у.
- средние квадратические отклонения по х и у.
Данные для расчета средних показателей и показателей вариации берем из вышеприведенной таблицы (графы 2, 3, 4, 5, 6).
Рассчитаем показатели 
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  .
.
Средние квадратические отклонения определим по формулам:
 ;
;  ;
;
 ;
;  .
.
Подставим необходимые данные в уравнение линейного коэффициента корреляции:
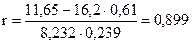 .
.
Значение линейного коэффициента корреляции показывает сильную прямую связь между объемом товарооборота и издержками обращения.
Вариант 1.
Задача 1. Имеются следующие данные по 25 заводам:
| Номер завода | Стоимость основных производственных фондов (среднегодовая), млн тг. | Выпуск продукции в сопоставимых ценах, млн тг. |
| 8,7 | 10,5 | |
| 3,6 | 5,2 | |
| 2,8 | 3,6 | |
| 10,7 | 19,9 | |
| 7,2 | 9,9 | |
| 6,3 | 10,2 | |
| 2,8 | 3,9 | |
| 4,2 | 5,1 | |
| 7,7 | 12,5 | |
| 5,6 | 6,8 | |
| 8,5 | 13,3 | |
| 8,8 | 12,9 | |
| 5,3 | 10,0 | |
| 8,4 | 14,7 | |
| 5,3 | 12,8 | |
| 3,1 | 3,5 | |
| 1,9 | 2,6 | |
| 2,7 | 5,5 | |
| 3,7 | 2,4 | |
| 1,3 | 2,5 | |
| 8,9 | 18,3 | |
| 9,1 | 19,6 | |
| 4,9 | 9,5 | |
| 5,0 | 9,3 | |
| 5,4 | 11,5 |
С целью выявления зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по стоимости основных фондов, образовав 5 групп заводов с равными интервалами.
Каждую группу охарактеризуйте:
1. числом заводов;
2. размером основных фондов – всего и в среднем на один завод;
3. выпуском продукции – всего и в среднем на один завод;
4. размером валовой продукции на 1 тг. основных фондов.
Результаты представьте в виде групповой таблицы. Сделайте краткие выводы.
Задача 2. Имеются следующие данные о посевной площади и урожайности озимой пшеницы по крестьянским хозяйствам:
| Номер хозяйства | Базисный год | Отчетный год | ||
| Урожайность, ц/га | Посевная площадь, га | Урожайность, ц/га | Валовой урожай, ц | |
| 18,3 | 19,1 | |||
| 20,1 | 20,5 | |||
| 21,3 | 21,4 |
Определите:
1. среднюю урожайность озимой пшеницы по хозяйствам для каждого года;
2. насколько изменилась урожайность в отчетном году по сравнению с базисным годом.
Какие виды средних следовало применить?
Задача 3. В результате 5%-го выборочного обследования изделий партии готовой продукции получены следующие данные о содержании сахара в образцах:
| Процент сахаристости | Число проб |
| До 10 | |
| 10-12 | |
| 12-14 | |
| 14-16 | |
| 16-18 | |
| Итого |
При условии, что продукция с сахаристостью до 10% относится к нестандартной, определите для всей партии:
1. с вероятностью 0,997 возможные пределы среднего процента сахаристости продукции;
2. с вероятностью 0,954 возможные пределы нестандартной продукции.
Обследование было произведено по схеме случайной (бесповторной) выборки.
Задача 4. Производство фосфора в РК характеризуется следующими показателями:
| Год | Производство фосфора, тонн |
Вычислите базисным и цепным способами:
1. абсолютные приросты, темпы роста, темпы прироста;
2. средний уровень ряда;
3. среднегодовой абсолютный прирост;
4. среднегодовые темпы роста и прироста.
Изобразите данные ряда динамики графически. Сделайте выводы.
Задача 5. Численность рабочих и служащих на промышленных предприятиях города характеризуется следующими данными (тыс. чел.):
1 января 198,5 1 июля 200,3
1 февраля 209,3 1 августа 211,1
1 марта 219,1 1 сентября 210,6
1 апреля 195,6 1 октября 209,8
1 мая 201,2 1 ноября 208,9
1 июня 199,7 1 декабря 205,8
1 января следующего года 203,6
Вычислите среднюю численность рабочих и служащих:
1. за первое полугодие;
2. за второе полугодие;
3. за год.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4 и 5 различны.
Задача 6. Реализация товаров в магазине характеризуется следующими данными:
| Товарная группа | Товарооборот, тыс. тг. | Изменение цен в отчетном году по сравнению с базисным годом, % | |
| базисный год | отчетный год | ||
| I | + 15,1 | ||
| II | без изменения | ||
| III | - 2,5 |
Вычислите:
1. индивидуальные и общий индексы цен;
2. общий индекс товарооборота в фактических ценах;
3. используя взаимосвязь индексов товарооборота, цен и физического объема товарооборота, исчислите общий индекс физического объёма товарооборота;
4. сумму экономии или дополнительного расхода от изменения цен, полученную
населением при покупке товаров в данном магазине.
Сделайте выводы.
Задача 7. Имеются следующие данные о реализации продукции:
| Товарная группа | Продано, тыс. тг. | Изменение количества проданных товаров в отчетном году по сравнению с базисным годом, % | |
| базисный год | отчетный год | ||
| I | - 7 | ||
| II | + 19 | ||
| III | без изменения |
Вычислите общий индекс физического объема товарооборота и общий индекс цен.
Сделайте выводы.
Задача 8. Себестоимость и объем продукции заводов характеризуются следующими данными:
| Изделие | Себестоимость единицы продукции, тг. | Выработано продукции, тыс. единиц | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Завод 1 | ||||
| Д -117 | 8,5 | 9,9 | ||
| АО - 30 | 8,1 | 7,9 | ||
| Завод 2 | ||||
| Д -117 | 8,2 | 8,7 |
На основе этих данных определите:
1. Для завода 1 (по трём видам изделий в целом):
а) общий индекс затрат на продукцию;
б) общий индекс себестоимости продукции;
в) общий индекс физического объёма продукции;
г) покажите взаимосвязь между этими индексами.
2. Для двух заводов вместе (по одинаковым изделиям):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс структуры;
г) покажите взаимосвязь между этими индексами.
Сделайте выводы.
Задача 9. На десяти различных участках производились опыты с целью изучения зависимости урожайности яровой пшеницы от глубины вспашки. В результате опыта получены следующие данные:
| Номер участка | Глубина вспашки, см | Средняя урожайность, ц/га |
| 10,1 | ||
| 9,6 | ||
| 11,3 | ||
| 10,0 | ||
| 12,6 | ||
| 8,7 | ||
| 8,9 | ||
| 9,3 | ||
| 10,3 | ||
| 9,7 |
Для выявления зависимости и тесноты связи между урожайностью яровой пшеницы и глубиной вспашки вычислите:
1. линейное уравнение связи;
2. линейный коэффициент корреляции.
Поясните смысл исчисленных показателей.
Вариант 2.
Задача 1. В отчетном периоде работа 24 заводов характеризуется следующими данными:
| Номер завода | Стоимость основных производственных фондов (среднегодовая), млн тг. | Выпуск продукции в сопоставимых ценах, млн тг. |
С целью выявления зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по стоимости основных фондов, образовав 5 групп заводов с равными интервалами.
Каждую группу охарактеризуйте:
1. числом заводов;
2. размером основных фондов – всего и в среднем на один завод;
3. выпуском продукции – всего и в среднем на один завод;
4. размером валовой продукции на 1 тг основных фондов.
Результаты представьте в виде групповой таблицы. Сделайте краткие выводы.
Задача 2. По четырем заводам, вырабатывающим продукцию «ВК-I», имеются следующие данные:
| Номер завода | Базисный год | Отчетный год | ||
| Затраты времени на единицу продукции, час. | Изготовлено продукции, шт. | Затраты времени на единицу продукции, час. | Затраты времени на всю продукцию, час. | |
Вычислите средние затраты времени на производство единицы продукции: 1) за базисный год; 2) за отчетный год. Укажите, какие виды средних применяли.
Задача 3. Для изучения выполнения нормы выработки рабочими-сдельщиками завода было проведено 10%-ное выборочное обследование (по методу случайного бесповторного отбора). Результаты обследования показали следующее распределение рабочих по проценту выполнения нормы выработки:
| Процент выполнения нормы | Число рабочих |
| До 90 | |
| 90-100 | |
| 100-110 | |
| 110-120 | |
| 120 и выше | |
| Итого: |
Исчислите для всех рабочих-сдельщиков завода:
1. с вероятностью 0,954 возможные пределы доли рабочих, выполняющих нормы выработки более чем на 100%;
2. с вероятностью 0,997 возможные пределы, в которых ожидается средний процент выполнения нормы выработки по заводу.
Указание: при расчете среднего процента выполнения нормы выработки в выборочной совокупности и среднего квадратического отклонения можно использовать простой способ или способ «моментов».
Задача 4. Производство цинка (необработанного) в РК характеризуется следующими данными:
| Год | Производство цинка, тонн |
Вычислите базисным и цепным способами:
1. абсолютные приросты, темпы роста, темпы прироста;
2. средний уровень ряда;
3. среднегодовой абсолютный прирост;
4. среднегодовые темпы роста и прироста.
Изобразите данные ряда динамики графически. Сделайте выводы.
Задача 5. Имеются следующие данные:
| Дата | 1 января | 1 февраля | 1 марта | 1 апреля | 1 мая | 1 июня | 1 июля |
| Остатки строительных материалов, тыс. тг. |
Вычислите среднемесячные остатки материала:
1. за I квартал;
2. за II квартал;
3. за полугодие.
Поясните, почему методы расчета средних уровней ряда динамики в задачах 4 и 5 различны.
Задача 6. Имеются следующие данные о товарообороте магазина:
| Товарная группа | Продано товаров в фактических ценах, тыс. тг. | Изменение цен в 3 кв. по сравнению с 1 кв., % | ||
| 1 квартал | 3 квартал | |||
| I | +20 | |||
| II | +4 | |||
| III | без изменения | |||
Вычислите:
1. индивидуальные и общий индексы цен;
2. общий индекс товарооборота в фактических ценах;
3. используя взаимосвязь индексов товарооборота, цен и физического объема товарооборота, исчислите общий индекс физического объёма товарооборота;
4. сумму экономии или дополнительного расхода от изменения цен, полученную населением при покупке товаров в данном магазине.
Сделайте выводы.
Задача 7. Продажа сельскохозяйственных продуктов характеризуется следующими показателями:
| Товарная группа | Продано товаров, тыс. тг. | Изменение количества проданных товаров в отчетном периоде к базисному периоду, % | |
| базисный период | отчетный период | ||
| I | - 9 | ||
| II | без изменения | ||
| III | + 15 |
Исчислите: индивидуальные и общий индексы физического объема товарооборота.
Задача 8. Имеются следующие данные о выработке продукции на двух заводах:
| Изделие | Себестоимость единицы продукции, тыс. тг. | Выработано продукции, единиц | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Завод 1 | ||||
| БК - 610 | 18,9 | |||
| У - 1 | 9,2 | |||
| АО - 620 | 18,0 | |||
| Завод 2 | ||||
| У - 1 | 8,7 |
На основе этих данных определите:
1. Для завода 1 (по трём видам изделий в целом):
а) общий индекс затрат на продукцию;
б) общий индекс себестоимости продукции;
в) общий индекс физического объёма продукции;
г) покажите взаимосвязь между этими индексами.
2. Для двух заводов вместе (по одинаковым изделиям):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс структуры;
г) покажите взаимосвязь между этими индексами.
Сделайте выводы.
Задача 9. На десяти различных участках производились опыты с целью изучения зависимости урожайности ржи озимой от глубины вспашки. В результате опыта получены следующие данные:
| Номер участка | Глубина вспашки, см | Средняя урожайность, ц/га |
| 8,8 | ||
| 9,7 | ||
| 11,4 | ||
| 9,6 | ||
| 12,7 | ||
| 8,8 | ||
| 8,7 | ||
| 9,2 | ||
| 10,4 | ||
| 9,7 |
Для изучения связи между урожайностью и глубиной вспашки вычислите:
1. линейное уравнение связи;
2. линейный коэффициент корреляции.
Поясните смысл исчисленных показателей.
Вариант 3.
Задача 1. Имеются следующие данные о работе 24 заводов:
| Номер завода | Стоимость основных производственных фондов (среднегодовая), млн тг. | Выпуск продукции в сопоставимых ценах, млн тг. |
| 2,0 | 1,5 | |
| 3,9 | 4,3 | |
| 3,3 | 6,4 | |
| 3,3 | 4,2 | |
| 3,0 | 1,5 | |
| 3,1 | 3,0 | |
| 3,1 | 2,6 | |
| 4,5 | 7,9 | |
| 3,1 | 3,6 | |
| 5,6 | 8,9 | |
| 3,5 | 2,6 | |
| 4,0 | 2,8 | |
| 1,2 | 1,6 | |
| 7,0 | 12,9 | |
| 4,5 | 5,5 | |
| 4,9 | 4,4 | |
| 2,8 | 2,8 | |
| 5,5 | 9,5 | |
| 6,6 | 11,9 | |
| 2,0 | 2,5 | |
| 4,7 | 3,5 | |
| 2,7 | 2,3 | |
| 3,0 | 3,3 | |
| 6,1 | 9,7 |
С целью выявления зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по стоимости основных фондов, образовав 5 групп заводов с равными интервалами.
Каждую группу охарактеризуйте:
1. числом заводов;
2. размером основных фондов – всего и в среднем на один завод;
3. выпуском продукции – всего и в среднем на один завод;
4. размером валовой продукции на 1 тг. основных фондов.
Результаты представьте в виде групповой таблицы. Сделайте краткие выводы.
Задача 2. По заводам, вырабатывающим продукцию «КС-I», имеются следующие данные:
| Номер завода | Базисный год | Отчетный год | ||
| Затраты времени на единицу продукции, час. | Изготовлено продукции, штук | Затраты времени на единицу продукции, час. | Затраты времени на всю продукцию, час. | |
Вычислите средние затраты времени на продукцию «КС-1» по заводам: 1. за базисный год;
2. за отчетный год.
Укажите, какие виды средних следует применить.
Задача 3. Для изучения среднего процента выполнения нормы выработки рабочими-сдельщиками завода было проведено 10-процентное выборочное обследование (по методу случайного бесповторного отбора). Результаты обследования показали следующее распределение рабочих по проценту выполнения нормы выработки:
| Процент выполнения нормы | Число рабочих |
| До 90 | |
| 90-100 | |
| 100-110 | |
| 110-120 | |
| 120 и выше | |
| Итого: |
Определите:
1.а) средний процент выполнения нормы выработки;
б) среднее квадратическое отклонение;
2. коэффициент вариации;
3. с вероятностью 0,954 возможные пределы, в которых ожидается средний процент выполнения нормы выработки рабочими-сдельщиками по заводу;
4. с вероятностью 0,997 возможные пределы удельного веса рабочих, перевыполняющих нормы свыше 100%.
Задача 4. Добыча сырой нефти в РК характеризуется следующими данными:
| Год | Добыча сырой нефти, тыс. тонн |
Вычислите базисным и цепным способами:
1. абсолютные приросты, темпы роста, темпы прироста;
2. средний уровень ряда;
3. среднегодовой абсолютный прирост;
4. среднегодовые темпы роста и прироста.
Изобразите данные ряда динамики графически. Сделайте выводы.
Задача 5. Имеются следующие данные о численности рабочих по цехам завода:
| Номер цеха | Число рабочих | |||
| 1 января | 1 февраля | 1 марта | 1 апреля | |
Вычислите среднесписочное число рабочих за квартал:
1. по каждому цеху;
2. по заводу в целом.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4 и 5 различны.
Задача 6. Имеются следующие данные о реализации товаров в магазине:
| Товарная группа | Товарооборот, тыс. тг. | Изменение цен в отчетном периоде по сравнению с базисным периодом, % | |
| базисный период | отчетный период | ||
| I | +5,5 | ||
| II | +18,5 | ||
| III | без изменения |
Вычислите:
1. индивидуальные индексы и общий индекс цен;
2. общий индекс товарооборота в фактических ценах;
3. используя взаимосвязь индексов товарооборота, цен и физического объема товарооборота, исчислите общий индекс физического объёма товарооборота;
4. сумму экономии или дополнительного расхода от изменения цен, полученную населением при покупке товаров в данном магазине.
Сделайте выводы.
Задача 7. Продажа сельскохозяйственных продуктов характеризуется следующими показателями:
| Товарная группа | Продано товаров, тыс. тг. | Изменение количества проданных товаров во II квартале по сравнению с I кварталом, % | |
| I квартал | II квартал | ||
| I | - 4 | ||
| II | без изменения | ||
| III | +15 |
Определите общий индекс физического объема товарооборота. Сделайте выводы.
Задача 8. Динамика себестоимости продукции заводов характеризуется следующими данными:
| Изделие | Себестоимость единицы продукции, тг. | Выработано продукции, единиц | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Завод 1 | ||||
| М - 404 | 16,0 | 15,6 | ||
| АТ-1 | 9,1 | 9,0 | ||
| Б - 405 | 14,0 | 13,2 | ||
| Завод 2 | ||||
| АТ-1 | 6,0 | 6,5 |
На основе этих данных определите:
1. Для завода 1 (по трём видам изделий в целом):
а) общий индекс затрат на продукцию;
б) общий индекс себестоимости продукции;
в) общий индекс физического объёма продукции;
г) покажите взаимосвязь между этими индексами.
2. Для двух заводов вместе (по одинаковым изделиям):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс структуры;
г) покажите взаимосвязь между этими индексами.
Сделайте выводы.
Задача 9. Имеются следующие данные по 10 заводам:
| Номер завода | Стоимость основных фондов, млн тг. | Выпуск продукции, млн тг. |
| 5,8 | ||
| 4,2 | ||
| 4,2 | ||
| 2,6 | ||
| 3,8 | ||
| 5,2 | ||
| 4,8 | ||
| 6,7 | ||
| 7,7 | ||
| 4,7 |
Вычислите:
1. для установления характера связи между стоимостью основных фондов и выпуском продукции – линейное уравнение связи;
2. для определения тесноты связи – линейный коэффициент корреляции.
Сделайте краткие выводы.
Вариант 4.
Задача 1. Имеются следующие данные о работе 24 заводов:
| Номер завода | Стоимость основных производственных фондов (среднегодовая), млн тг. | Выпуск продукции в сопоставимых ценах, млн тг. |
| 2,3 | 1,3 | |
| 3,8 | 4,3 | |
| 3,3 | 6,4 | |
| 3,1 | 4,1 | |
| 3,0 | 1,4 | |
| 3,1 | 3,0 | |
| 3,2 | 2,6 | |
| 4,3 | 7,8 | |
| 3,1 | 3,5 | |
| 5,5 | 8,7 | |
| 3,6 | 2,5 | |
| 4,1 | 2,7 | |
| 1,3 | 1,6 | |
| 7,0 | 13,0 | |
| 4,6 | 5,5 | |
| 4,8 | 4,3 | |
| 2,9 | 2,9 | |
| 5,4 | 9,5 | |
| 6,5 | 11,8 | |
| 2,1 | 2,5 | |
| 4,8 | 3,4 | |
| 2,8 | 2,2 | |
| 3,1 | 3,4 | |
| 6,3 | 9,7 |
С целью выявления зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по стоимости основных фондов, образовав 5 групп заводов с равными интервалами.
Каждую группу охарактеризуйте:
1. числом заводов;
2. размером основных фондов – всего и в среднем на один завод;
3. выпуском продукции – всего и в среднем на один завод;
4. размером валовой продукции на 1 тг. основных фондов.
Результаты представьте в виде групповой таблицы. Сделайте краткие выводы.
Задача 2. По заводам, вырабатывающим продукцию «КС-1», имеются следующие данные:
| Номер завода | Базисный год | Отчетный год | ||
| Затраты времени на единицу продукции, час. | Изготовлено продукции, штук | Затраты времени на единицу продукции, час. | Затраты времени на всю продукцию, час. | |
Вычислите средние затраты времени на продукцию «КС-I» по трем заводам:
1. за базисный год;
2. за отчетный год.
Укажите, какие виды средних следует применить.
Задача 3. Для изучения среднего процента выполнения нормы выработки рабочими-сдельщиками завода было проведено 5-процентное выборочное обследование (по методу случайного бесповторного отбора). Результаты обследования показали следующее распределение рабочих по проценту выполнения нормы выработки:
| Процент выполнения нормы | Число рабочих |
| До 90 | |
| 90-100 | |
| 100-110 | |
| 110-120 | |
| 120 и выше | |
| Итого: |
Определите:
1. а) средний процент выполнения норм выработки;
б) среднее квадратическое отклонение;
2. коэффициент вариации;
3. с вероятностью 0,954 возможные пределы, в которых ожидается средний процент выполнения нормы выработки рабочими-сдельщиками по заводу;
4. с вероятностью 0,997 возможные пределы удельного веса рабочих, перевыполняющих нормы свыше 100%.
Задача 4. Добыча природного газа (включая газ нефтяной попутный) в РК характеризуется следующими данными:
| Год | Добыча природного газа, млн. куб. м |
Вычислите базисным и цепным способами:
1. абсолютные приросты, темпы роста, темпы прироста;
2. средний уровень ряда;
3. среднегодовой абсолютный прирост;
4. среднегодовые темпы роста и прироста.
Изобразите данные ряда динамики графически. Сделайте выводы.
Задача 5. Имеются следующие данные о численности рабочих по цехам завода:
| Номер цеха | Число рабочих | |||
| 1 января | 1 февраля | 1 марта | 1 апреля | |
Вычислите среднесписочное число рабочих за I квартал:
1. по каждому цеху;
2. по заводу в целом.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4 и 5 различны.
Задача 6. Имеются следующие данные о реализации товаров в магазине:
| Товарная группа | Товарооборот, тыс. тг. | Изменение цен в отчетном периоде по сравнению с базисным, % | |
| базисный период | отчетный период | ||
| I | + 10 | ||
| II | + 18 | ||
| III | без изменения |
Вычислите:
1. индивидуальные индексы и общий индекс цен;
2. общий индекс товарооборота в фактических ценах;
3. используя взаимосвязь индексов товарооборота, цен и физического объема товарооборота, исчислите общий индекс физического объёма товарооборота;
4. сумму экономии или дополнительного расхода от изменения цен, полученную населением при покупке товаров в данном магазине.
Сделайте выводы.
Задача 7. Продажа сельскохозяйственных продуктов характеризуется следующими показателями:
| Товарная группа | Продано товаров, тыс. тг. | Изменение количества проданных товаров в отч. периоде по сравнению с баз. периодом, % | ||
| базисный период | отчетный период
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-26 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |