Наиболее известным критерием обнаружения автокорреляции первого порядка является критерий Дарбина- Уотсона и расчет величины
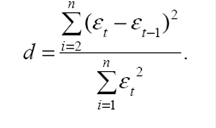(2.3.1)
Согласно (2.3.1) величина d есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии. Значение критерия Дарбина – Уотсона указывается наряду с коэффициентом детерминации, значениями t- и F- критериев.
Коэффициент автокорреляции остатков первого порядка определяется как
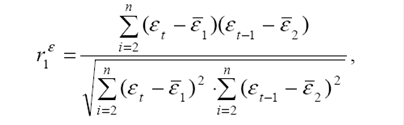
где
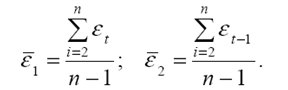(2.3.2)
Между критерием Дарбина–Уотсона и коэффициентом автокорреляции остатков первого порядка имеет место следующее соотношение:
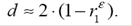
Таким образом, если в остатках существует полная положительная автокорреляция и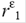 
= 1, то d = 0. Если в остатках полная отрицательная автокорреляция, то 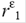= – 1 и, следовательно, d = 4. Если автокорреляция остатков отсутствует, то 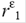= 0 и d = 2. Следовательно, 0 <d <4.
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина–Уотсона следующий. Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков. Альтернативные гипотезы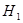 
и 
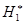состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по таблице (приложение А) определяются критические значения критерия Дарбина–Уотсона 
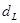и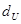 
для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости a. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1– a) рассматривается на рис. 2.3.
Рис. 2.3.1. Механизм проверки гипотезы о наличии автокорреляции остатков
Если фактическое значение критерия Дарбина – Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу H0.
|
|
Пример 2.3.1. Проверка гипотезы о наличии автокорреляции в остатках.
Исходные данные, значения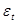 
и результаты промежуточных расчетов
представлены в табл. 2.3.1.
Таблица 2.3.1. - Расчет критерия Дарбина–Уотсона для модели зависимости потребления от дохода
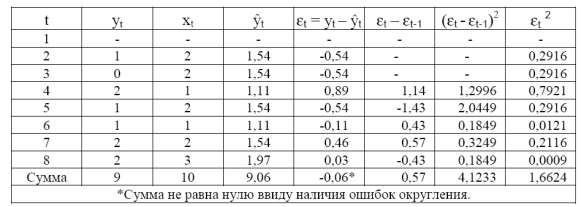
Фактическое значение критерия Дарбина–Уотсона для этой модели составляет d = 4,1233/1,6624 = 2,48. Сформулируем гипотезы:
Н0 – в остатках нет автокорреляции;
Н1 – в остатках есть положительная автокорреляция;
Н1* – в остатках есть отрицательная автокорреляция.
Зададим уровень значимости a = 0,05. По таблицам значений критерия Дарбина–Уотсона определим для числа наблюдений n = 7 и числа независимых переменных модели k ' = 1 критические d L = 0,700 и d U = 1,356. Получим следующие промежутки внутри интервала [0;4]
Рис. 2.3.2. Промежутки внутри интервала [0; 4]
Фактическое значение d = 2,48 попадает в промежуток от 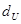до 4 – 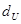. Следовательно, нет оснований отклонять гипотезу H0 об отсутствии автокорреляции в остатках.
Пример 2.3.2. В таблице 2.3.2. приведены данные, отражающие спрос на некоторый товар за восьмилетний период, т.е. временной ряд спроса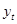 
Таблица 2.3.2.
Выявить на уровне значимости 0,05 наличие автокорреляции в остатках для временного ряда.
Получили уравнение тренда:
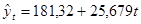
В таблице 2.3.3 приведены необходимые вычисления
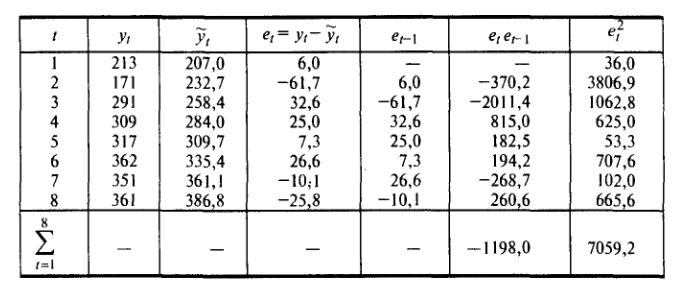
Таблица 2.3.3
По формуле вычислили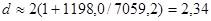 
По таблице критических точек при n=15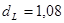 
, 
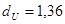, т.е. фактически найденное d=2.34 находится в пределах от 
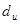до 4-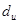 
(1.36<d<2.64). При n<15 критических значений d-статистики в таблице нет, но судя по тенденции их изменений с уменьшением n, можно предполагать, что найденное значение останется в интервале (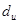,4- 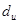), т.е. для рассматриваемого временного ряда спроса на уровне значимости 0,005 гипотеза об отсутствии автокорреляции остатков не отвергается.
|
|
Есть несколько существенных ограничений на применение критерия Дарбина–Уотсона. Во-первых, он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака, т. е. к моделям авторегрессии. Во-вторых, методика расчета и использования критерия Дарбина – Уотсона направлена только на выявление автокорреляции остатков первого порядка. При проверке остатков на автокорреляцию более высоких порядков следует применять другие методы. В-третьих, критерий Дарбина–Уотсона дает достоверные результаты только для больших выборок.