Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении
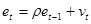, t =1,…,n (2.4.1)
(где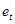 
-остатки регрессии, полученные обычным методом наименьших квадратов), коэффициент 
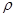окажется значимо отличающимся от нуля.
Практическое применение теста заключается в оценивании методом наименьших квадратов регрессии (2.4.1)
Преимущество теста Бреуша–Годфри по сравнению с тестом Дарбина-Уотсона содержит зону неопределенности для значений статистики d. Другим преимуществом теста является возможность обобщения: в число регрессоров могут быть включены не только остатки с лагом 1, но и с лагом 2,3 и т.д., что позволяет выявить корреляцию не только между соседними, но и между более отдаленными наблюдениями.
Рассмотрим в качестве примера (2.4) временной ряд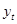 
- ряд последовательных значений курса ценной бумаги А, наблюдаемых в моменты времени 1,…,100. Результаты наблюдений графически изображены на рисунке 2.4.
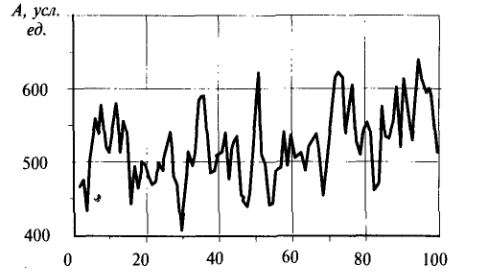
Рис.2.4
Очевидно, курс ценной бумаги А имеет тенденцию к росту, что можно проследить на графике.
Оценивая обычным методом наименьших квадратов зависимость курса наблюдений (т.е. от времени), получим следующие результаты:
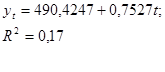
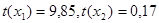
Имеет место положительная автокорреляция (т.к. результаты предыдущих торгов оказывают влияние на результаты последующих)
Проверим это с помощью теста Бреуша-Годфри.
Рассмотрим авторегрессионную зависимость остатков от их предыдущих значений, используя авторегрессионную модель р-го порядка. Применяя МНК, получим:
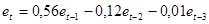(2.4.2)
(0,10) (0,12) (0,10)
Как видно, значимым оказывается только регрессор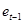 
,т.е. существенное влияние на результат наблюдения 
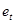оказывает только одно предыдущее значение 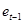. Положительность оценки соответствующего коэффициента регрессии указывает на положительную корреляцию между ошибками регрессии 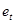и .
|
|
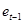Q-тест Льюинга-Бокса
Тест основан на рассмотрении выборочных автокорреляционной и частной автокорреляционной функцией временного ряда.
Если ряд стационарный, то, как можно доказать, выборочный частный коэффициент корреляции совпадает с оценкой обычного метода наименьших квадратов коэффициента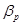 
в авторегрессионной модели AR(p):
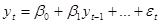
Это утверждение лежит в основе вычисления значений частной автокорреляционной функции.
Очевидно, что в случае отсутствия автокорреляции все значения автокорреляционной функции равны нулю. Разумеется, ее выборочные значения окажутся отличными от нуля, но в этом случае отличие не должно быть существенным. На этой идее и основан тест Льюинга-Бокса, проверяющий гипотезу об отсутствии автокорреляции.
Статистика Льюинга-Бокса имеет вид:
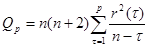(2.5)
Можно доказать, что если верна гипотеза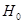 
о равенстве нулю всех коэффициентов корреляции 
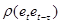, где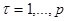 
, то статистика 
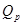имеет распределение 
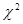с р степенями свободы.
Пример 2.5 Проверить гипотезу об отсутствии автокорреляции в модели зависимости курса ценной бумаги А от времени t (пример 2.4)
Значение d-статистики Дарбина-Уотсона, примерно равное единице, дает оценку коэффициента корреляции между 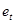и 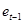, т.е. r(1)=0,5/
Отсюда по формуле 2.5
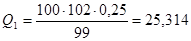
Так как фактическое значение статистики больше критического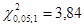 
, то гипотеза 
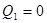отвергается
Заметим, что гипотеза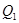 
=0 и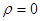 
о равенстве нулю коэффициента 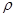в уравнении 2.4.1 представляют собой по сути одно и то же утверждение об отсутствии авторегрессии первого порядка. Результат тестирования этих гипотез должен совпадать с выводом, к которому приводит значение статистики Дарбина- Уотсона.
|
|