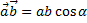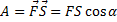Закон сохранения механической энергии.

Законы сохранения в механике

Импульс (количество движения) материальной точки. Импульс силы. Связь между приращением импульса материальной точки и импульсом силы. Импульс системы материальных точек. Центр масс. Закон сохранения импульса. Реактивное движение.

Механическая работа. Мощность. Энергия. Единицы измерения работы и мощности.

Кинетическая энергия материальной точки и системы материальных точек. Связь между приращением кинетической энергии тела и работой приложенных к телу сил.

Потенциальная энергия. Потенциальная энергия тел вблизи поверхности Земли. Потенциальная энергия упруго деформированного тела.

Закон сохранения механической энергии.

Пусть на тело массой в течение времени действует постоянная сила . Под действием этой силы тело движется с ускорением

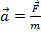
Учитывая, что

получим, что (1)

Произведение массы тела на его скорость называется импульсом тела (или количеством движения).

Импульс тела – векторная величина, в системе СИ единица измерения – 1

Формула (1) выражает закон изменения импульса тела: изменение импульса тела под действием постоянной силы равно произведению силы на время её действия.

Произведение вектора силы на время её действия называют импульсом силы; это векторная физическая величина, характеризующая в поступательном движении меру воздействия силы на тело за данный промежуток времени.

До сих пор мы рассматривали действия сил на одно тело, однако чаще мы встречаемся с группой тел, взаимодействующих друг с другом. Такую группу тел мы будем называть системой тел. Если на тела системы не действуют никакие внешние силы, то система называется замкнутой.

Для простоты рассмотрим замкнутую систему, состоящую из двух тел, массы которых , и эти тела движутся со скоростями соответственно. Каждое из тел имеет импульс и . Векторная сумма импульсов называется импульсом системы.

Пусть при своем движении этих тел происходит их соударение (аналогично соударению двух движущихся бильярдных шаров). В результате соударения импульс каждого из тел изменится, т.к. изменятся, по крайней мере, направления скоростей этих тел (а могут измениться и величины скоростей). Пусть в результате этого соударения тела приобрели скорости и . Тогда для первого тела

- сила, с которой второй шар ударил первый, - время соударения.

Для второго шара

Где - сила, с которой первый шар ударил второй, - время соударения.

Но согласно третьему закону Ньютона при соударении шаров , а одинаково для обоих шаров.

Тогда

),

 

Мы получили, что сумма импульсов тел системы до взаимодействия равна сумме импульсов тел системы после взаимодействия, а значит, импульс системы не изменился.

Можно доказать, что для замкнутой системы, состоящей из любого числа тел, суммарный импульс системы остаётся постоянным в любой момент времени. Тогда можно сформулировать закон сохранения импульса для замкнутой системы: импульс замкнутой системы неизменен.

Всеобщность закона сохранения импульсов заключается в том, что он применим не только в механике, но и для любых систем тел и любых процессов, происходящих с телами системы, при условии замкнутости системы.

Импульс системы неизменим, в случае если тела системы разрушаются (граната разлетается на осколки), если в результате химических реакций из одних веществ образуются другие, или одни элементарные частицы обращаются в другие.

Если система состоит из одного тела, то закон сохранения импульса для него равносилен первому закону Ньютона (закон инерции).

Реактивным движением называют движение тела, возникающее при отделении какой-либо его части. Движение большинства современных самолетов является реактивным т.к. возникает благодаря истечению с огромной скоростью нагретых в двигателе газов. Также движутся и ракеты, выбрасывая из сопла продукты сгорания топлива. Примером реактивного движения может служить и отдача ствола орудия при выстреле.

Силу, действующую на тело при таком движении. Называют реактивной.

Рассмотрим систему “ракета с вытекающими из нее газами”, движущуюся в космическом пространстве вдали от других тел;в таких условиях систему можно условно считать замкнутой и применить закон сохранения импульса.

Пусть в некоторый момент времени ракета имеет массу , скорость и импульс ; при движении из сопла ракеты истекают продукты сгорания в количестве . Тогда спустя время имеем: )+n ), где

=-n

Если разделить обе части уравнения на , то мы получим уравнение Мещерского

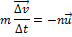
, => - реактивная сила равная произведению количества истекающих за единицу времени газов умноженную на скорость истечения газов и эта сила направлена противоположно скорости истечения газов.

Существует два типа реактивных двигателей – ракетные и воздушно-реактивные. Ракетный двигатель создает реактивную силу, выбрасывая из сопла продукты сгорания топлива и окислителя

 

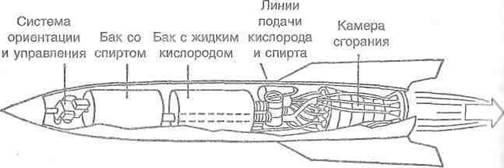
У воздушно-реактивных двигателей для горения используется кислород, который содержится в атмосфере. Эти двигатели оснащены компрессорами, которые засасывают воздух лопастями компрессора и сжимают его, подавая в камеру сгорания. Продукты сгорания с огромной скоростью вырываются из сопла создавая реактивную силу и вращая турбину и ось, на которой находятся лопасти компрессора.

Перед тем как дать определение новой физической величины – механической работы, мы дадим определение скалярного произведения векторов.

Скалярным произведение двух векторов называют скалярную величину, численно равную произведению длин этих векторов на косинус угла между ними.

 

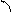Пусть на тело действует сила 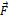, и под действием этой силы тело совершает перемещение .

 

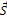Механической работой, которую совершила сила 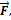называют скалярное произведение векторов силы 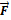и перемещения на протяжении которого действовала сила

 

Если направления силы и перемещения совпадают, то работа считается положительной, если противоположны (90 , то отрицательной. Например, работа сил трения всегда отрицательна.

В системе СИ единицей измерения работы является 1 Дж.

Для характеристики действия различных сил важна не только работа, которую совершают эти силы, но и время, в течение которого эта работа совершается.

Отношение работы, совершаемой силой, к промежутку времени, в течение которого совершалась эта работа, называется мощностью.

В системе СИ единицей измерения мощности является 1Вт.

Простые жизненные наблюдения показывают, что совершение работы всегда связано с расходом какой-либо энергии. Поэтому можно определить энергию как способность тела совершать работу.

В механике различают 3 вида энергии:

1. Энергия, которой обладают тела, находящиеся в гравитационном поле Земли.

2. Энергия, связанная с деформациями тела.

3. Энергия, связанная с движением тела.

Пусть тело массой свободно падает с высоты без начальной скорости. В этом случае сила тяжести совершает работу

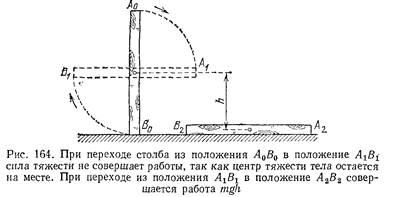
Под потенциальной энергией тела в гравитационном поле Земли понимают произведение массы тела на ускорение свободного падения и высоту тела над неким горизонтальным уровнем, который мы считаем соответствующим нулевому значению потенциальной энергии.

За нулевой уровень потенциальной энергии мы условно принимаем, горизонтальный уровень, удобный нам при рассмотрении той или иной задачи. Тело падает на землю – удобно считать за “0” поверхность земли. Тело падает на стол – поверхность стола, опускается гиря в часах – за “0” удобно взять положение нижней точки гири.

Во всех физических явлениях важно не абсолютное значение потенциальной энергии, а её изменение. А это изменение потенциальной энергии будет одинаковым относительно любого нулевого уровня. При этом если тело имеет значительные размеры относительно высоты над нулевым уровнен, то за высоту тела следует брать высоту центра масс.

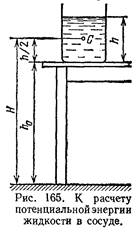
Энергию упруго деформированного тела также называют потенциальной (или упругой) энергией, т.к. она зависит от взаимного расположения частей тела (например, витков пружины). Работа, которую может совершить растянутая или сжатая пружина, зависит только от начального и конечного растяжений пружины.

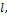Найдем работу, которую совершает растянутая пружина, при этом заметим, что сила упругости при совершении работы не является постоянной, а изменяется с изменением удлинения пружины. В начальный момент = . При возвращении пружины в свободное состояние = 0. Т.к. линейно зависит от то среднее значение силы упругости

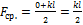
При этом возвращаясь в свободное состояние, она перемещает груз на расстояние 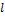(трением груза о стол пренебрегаем). Тогда работа

Таким образом, потенциальная энергия упругой пружины, за счет которой совершена работа

Тела могут обладать некоторым “ запасом работы”, т.е. обладать энергией не потому, что они занимают определенное положение в пространстве или деформированы, но и потому, что они обладают скоростью. Санки, имеющие скорость у основания горки, могут подняться по ней на некоторую высоту, совершая работу против сил тяжести и трения; когда двигающийся накатом вагон ударяет своими буферами о буфера другого вагона, то пружины буферов сжимаются, т.е. совершается работа против сил упругости пружин.

Всякий раз, когда тело совершает работу благодаря тому, что оно движется, скорость его движения уменьшается. Если скорость тела уменьшится до нуля, то запас “ способности совершать работу” будет исчерпан, и энергия, которой обладает тело, благодаря своему движению станет равна нулю. Энергию, которой обладает тело, потому что оно движется, называют кинетической энергией или энергией движения.

Пусть на покоящееся тело массой начинает действовать сила , под действием которой оно будет двигаться с ускорением . Пройдя расстояние тело приобретает скорость , тогда

Работа этой силы .

То чно также если бы мы на тело, имеющее скорость начали бы действовать с силой , направленной против движения тела и остановили бы его, то работа этой тормозящей силы была бы также .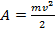

Значит кинетическая энергия движущегося тела

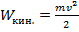
Таким образом всякое тело может обладать механической энергией в виде потенциальной (энергией положения) и в виде кинетической (энергией движения).

В системе СИ единицей измерения энергией является 1 Дж.

Часто тело обладает как кинетической, так и потенциальной энергиями. Сумма всех механических энергий, которыми обладает тело, называется полной энергией.

Опыты и теоретические расчеты показывают, если на тело не действуют силы трения или сопротивления среды, то его полная энергия остается постоянной в любой момент трения. В этом и состоит закон сохранения механической энергии.