Дана схема системы подачи и распределения воды:
| ▲ |
Таблица №1
| № участка | Длина участка l, м | Диаметр труб d, мм | Материал | Удельное гидравлическое сопротивление
 ,
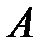(л/c)-2
| Гидравлическое сопротивление участка
 ,
м ·(л/c)-2
| Расход на участке x, л/с | Потери напора на участке x ΔH, м |
| чугун | 0,2189·10-6 | 55.76·10-6 | 0,59 | ||||
| чугун | 0,9485·10-6 | 168.7·10-6 | 0,59 | ||||
| чугун | 2,528·10-6 | 665.2·10-6 | 70,91 | 1,3 | |||
| чугун | 8,092·-6 | 2615.5·10-6 | 48,91 | 3,99 | |||
| чугун | 37,11·10-6 | 10062·10-6 | 4,54 | ||||
| чугун | 37,11·10-6 | 5869.5·10-6 | 5,63 | 0,41 | |||
| чугун | 8,092·10-6 | 2615.5·10-6 | 33,63 | 3,84 | |||
| чугун | 8,-92·10-6 | 1830.85·10-6 | 9,46 | 0,26 | |||
| чугун | 2,528·10-6 | 665.2·10-6 | 62,09 | 2,96 |
Таблица №2
| Номер узла | Отбор в узле Q, л/c | Давление в узле P, Па | Геод. Отметка z, м | Напор в узле H, м |
| -133 | ||||
| 79,95 | ||||
| 22,0 | 78,84 | |||
| 24,0 | 76,97 | |||
| 25,0 | 70,39 | |||
| 15,0 | 66,08 | |||
| 28,0 | 70,84 | |||
| 19,0 | 77,47 |
Требуется:
1. Рассчитать расход на каждом участке; напор в узлах.
2. Рассчитать потери напора на участках; давление в каждом узле.
3. Рассчитать потери напора по каждому кольцу.
4. Построить напорную линию. Определить пьезометрические уклоны в каждом узле.
Схема системы подачи и распределения воды: в окружностях указаны номера узлов; над дугами – номера дуг; на дуге 1 – насосная станция; направление дуги указывает направление потока
Напорно-расходная характеристика насоса:
1. Получение напоров в узлах и расходов по участкам Получение напоров в узлах и расходов по участкам.
Составим уравнение баланса расходов в каждом узле нашей сети.
1. х1-Q1=0 х1=Q1 х1 Q1
2. x2+x9 +Q2-x1=0 x2+x9-x1=-Q2 x2 -Q2
3. x3-x2+Q3=0 x3-x2=-Q3 x3 -Q3
(1) 4. x4-x3-x8+Q4=0 → x4-x3-x8=-Q4 x4 b= -Q4
5. x5-x4-x6+Q5=0 x5-x4-x6=-Q5 x= x5 -Q5
6. -x5+Q6=0 -x5=-Q6 x6 -Q6
7. x6-x7 +Q7=0 x6-x7=-Q7 x7 -Q7
8. x7+x8+x9+Q8=0 x7+x8+x9=-Q8 x8 -Q8
x9
Построение математической модели кольцевого трубопровода.
Составим матрицу полученной системы А (матрица инцинденций).
| А | |||||||||
| участок узел | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | -1 | ||||||||
| -1 | -1 | ||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 |
Ах=b
Система линейно-зависима, т.к. ∑Qi=0 и при сложении всех уравнений системы (1) получили 0=0, поэтому одно уравнение можно вычеркнуть. Получаем усеченную матрицу А и усеченный вектор b.
| А | |||||||||
| участок узел | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | -1 | ||||||||
| -1 | -1 | ||||||||
| -1 | |||||||||
| -1 |
Q1
-Q2
-Q3
b= -Q4
-Q5
-Q6
-Q7
Тогда уравнение баланса расходов примет вид: Ax=b. (2)
2. Составляем уравнение Бернулли для каждого участка гидравлической системы, например, для первого участка.
На первом участке получаем следующее уравнение:
u1-u2=y1,
где u1, u2 – пьезометрические напоры в 1 и 2 узлах; y1 - потери напора на первом участке, y1=y1длина+y1насос=S1|x1|x1-H0-SH|x1|x1=(S1+Sн)|x1|x1-H0 (потери напора для насоса берутся со знаком «-», т.к. дуга моделирует насос).
Аналогично, составляя уравнения Бернулли для всех остальных участков, получим систему уравнений (3).
1. u1-u2=y1; y1= (S1+Sн)|x1|x1-H0 u1 y1
2. u2-u3 =y2; y2=S2|x2|x2 u2 y2
3. u3-u4 =y3; y3=S3|x3|x3 u3 y3
4. u4-u5 =y4; y4=S4|x4|x4 u4 y4
(3) 5. u5-u6 =y5; y5=S5|x5|x5 u= u5 y= y5
6. u7-u5 =y6; y6=S6|x6|x6 u6 y6
7. u8-u7 =y7; y7=S7|x7|x7 u7 y7
8. u8-u4 =y8; y8=S8|x8|x8 u8 y8
9. u2-u8 =y9; y9=S9|x9|x9 y9
(S1+Sн)|x1|x1
S2|x2|x2
S3|x3|x3
S4|x4|x4
f(x)= S5|x5|x5
S6|x6|x6
S7|x7|x7
S8|x8|x8
S9|x9|x9
Матрица системы (3) является транспонированной матрицей матрицы А.
Выпишем матрицу AT – транспонированную матрицу.
| AT | ||||||||
| участок узел | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 |
Тогда в матричном виде получаем:
ATu=f(x). (4)
3. Для нахождения неизвестных u и x имеем следующую систему нелинейных уравнений:
Ax=b (2)
ATu=f(x). (4)
Из составленных уравнений мы получили 9 переменных x и 8 переменных u, всего 9+8=17 – переменных и 7+9=16 - уравнений. Для решения системы уравнений (2) и (4) необходимо задать значение одной из переменных, в данном случае по условию задан напор в первом узле, равный Н1=25 м. Воспользовавшись программой ИСИГР, находим искомые значения расхода на участке x, потерь напора на участке x, давления в узле и напора в узле и заносим данные в таблицы 1 и 2.
Рис. 6. Схема задачи, решённой в программе ИСИГР
4.Строим пьезометрическую линию трубопровода с 1 до 6 узла, воспользовавшись программой ИСИГР
Рис. 7. Напорная характеристика трубопровода с 1 до 6 узла
5. Потери напора по кольцу. Находим алгебраическую сумму потерь напора в кольцах, которая должна быть равна нулю: 
. Сеть считается рассчитанной, если при данных расходах по ветвям кольцевой сети потери напора по одной ветви кольца равны потерям напора по другой его ветви.
В нашей сети мы можем выделить три кольца, по которым делаем расчеты.
1) Рассчитаем потери напора по кольцу 2-3-4-8.
Поток в точке 2 разделяется на два направления, а в точке 4 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 2 до точки 4 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:
ΔНкольцо1 = (Н2–Н3) + (Н3–Н4) – (Н8–Н4) – (Н2–Н8) = 0.
Т.е. при рассмотрении движения воды относительно кольца мы принимаем положительными потери напора, возникающие при движении воды по ходу часовой стрелки, а отрицательными – против часовой стрелки.
2) Рассчитаем потери напора по кольцу 4-5-7-8.
Поток в точке 8 разделяется на два направления, а в точке 5 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 8 до точки 5 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:
ΔНкольцо2 = (Н8–Н4) + (Н4–Н5) – (Н7–Н5) – (Н8–Н7) = 0.
3)
Поток в точке 2 разделяется на два направления, а в точке 5 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 2 до точки 5 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:
ΔНкольцо3 = (Н2–Н3) + (Н3–Н4) + (Н4–Н5) – (Н7–Н5) – (Н8–Н7) – (Н2–Н8) = 0.
Сумма потерь напора по каждому кольцу равна нулю.
4. Определение давления в узлах кольцевой цепи
Избыточное давление определяется из определения полного напора:
,
где Hn – напор в соответствующем узле, zn 
геометрическая высота соответствующего узла, 
удельный вес (= 9,81 
103, Н/м3).
= 9,81 103 (15,00 
0) = 117720 Па;
= 9,81 103 (84.93 0) = 778914 Па;
= 9,81 103 (83.63 0) = 759784 Па;
= 9,81 103 (81.71 0) = 733101 Па;
= 9,81 103 (77.72 0) = 618206 Па;
= 9,81 103 (73.18 0) = 624995Па;
= 9,81 103 (78.13 0) = 687288 Па;
= 9,81 103 (81.97 0) = 737225 Па.
5. Гидравлический уклон 
Гидравлический уклон выражает потерю полной удельной энергии (гидродинамического напора), приходящуюся на единицу длины потока.
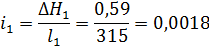
Заключение.
В нашей курсовой работе мы должны были решить три задачи 1. сделать гидравлический расчёт короткого трубопровода, 2. Определение высоты всасывания насоса, и 3. гидравлический расчет кольцевой замкнутой водопроводной сети.
В первой задаче мы нашли значения потерь напора в трубопроводах на всех участках: потери на выходе из бака, потери по длине, на внезапное расширение и на поворот. По данным расчётам построили напорную и пьезометрическую линии напорную характеристику трубопровода.
Во второй задаче найдены напоры в узлах трубопроводной сети, расходы и потери напора на участках. Также были подсчитаны суммы потерь напоров в циклах, гидравлические уклоны участков и пьезометрическая линия выбранного участка трубопровода. По этим подсчетам был сделан вывод: сумма потерь напоров вдоль любого цикла равна нулю. Найдены давления в каждом узле трубопроводной сети при заданных геометрических высотах в узлах.
Во третье задаче нашли потери в узлах трубопроводной сети, расходы на участках и потери напора в узлах, посчитали суммы потерь напоров в циклах. По этим расчётам сделали вывод: сумма потерь напора вдоль любого цикла равняется нулю, нашли давления в каждом узле при заданной геометрической высоте.
Список использованной литературы.
1. Сомов М.А., Журба М.Г. Водоснабжение. Том 1. Системы забора, подачи и распределения воды: Учебник для вузов. ‒ М.: Издательство АСВ, 2010. ‒ 262с.
2. Сайриддинов С.Ш. Гидравлика систем водоснабжения и водоотведения: Учеб. пособие. – М.: Издательство АСВ, 2008. – 352 с.
3. Шевелев Ф.А., Шевелев А.Ф. Таблицы для гидравлического расчета водопроводных труб: Справ. пособие. – 8-е изд., перераб. и доп. М.: Стройиздат,2008.–352 с.
4. Чугаев Р.Р. Гидравлика М.: 2008. – 670 с.
5. Ухин Б.В., Гусев А. А. Гидравлика ИНФРА-М.: 2010 г. – 432 с.