Магнитное поле тока. Электромагнитная индукция.

· dB = µ₀µ I d 𝓁sinα/4π r ²,Закон Био – Савара – Лапласа, где – магнитная индукция поля, создаваемая элементом проводника длиной dl с током I; r – радиус–вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция, α – угол между радиус–вектором и направлением тока в элементе проводника.

· B = ∑ B_i – принцип суперпозиции (наложения) магнитных полей, где B – магнитная индукция результирующего поля; B_i – магнитные индукции создаваемых полей.

· B = µ₀µ H – связь магнитной индукции B и напряжённости H магнитного поля, где магнитная постоянная µ₀ = 4π · 10 ^{– 7} Гн/м, µ − магнитная проницаемость среды.

· B = µ₀µ I / 2 π а – индукция магнитного поля, создаваемого прямым бесконечно длинным током, где I – сила тока; а – расстояние от проводника с током до точки, в которой определяется значение индукции В.

· · B = µ₀µ I (cosα₁–cosα₂)/4π а – индукция магнитного поля, созданного током, протекающим по отрезку прямолинейного проводника, где I – сила тока в проводнике; а – расстояние по нормали от проводника до точки «a », в которой необходимо определить В; α₁, α₂ – углы, образованные направлением тока в проводнике и радиусами–векторами, проведенными от концов проводника к точке «a ».

· B = µ₀µ I / 2а – индукция магнитного поля в центре кругового проводника с током, создающим это магнитное поле, где I – сила тока, а – радиус витка.

· · B = – магнитная индукция на оси кругового тока, где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

· · = µ_o ∑ I_k – закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора B), где – алгебраическая сумма токов, охватываемых контуром.

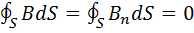· · – теорема Гаусса для поля с магнитной индукцией B.

· B = µ₀ I N / 𝓁 – магнитная индукция поля внутри соленоида (в вакууме), имеющего N витков и длину 𝓁.

· B = µ₀ I N / 2 π r – магнитная индукция внутри тороида (в вакууме), где r – радиус осевой линии тороида.

· Ф = B S cosα – поток вектора магнитной индукции (магнитный поток) в случае однородного магнитного поля и плоской поверхности, где S – площадь контура; α– угол между нормалью к плоскости и вектором магнитной индукции.

· · Ф = – магнитный поток в случае неоднородного магнитного поля и произвольной поверхности.

· L = µ₀µ N ² S / 𝓁 – индуктивность соленоида, где N – число витков в соленоиде; ℓ − длина соленоида; S – площадь поперечного сечения соленоида.

· – магнитный поток, создаваемый током I в контуре с индуктивностью L.

· = B S N – потокосцепление с соленоидом, помещенным во внешнее магнитное поле, где В – индукция магнитного поля; S – площадь поперечного сечения соленоида; N – число витков в соленоиде.

· µ₀µ N ² S I / 𝓁– собственное потокосцепление соленоида, где I – сила тока в соленоиде; N – число витков в соленоиде; 𝓁 – длина соленоида; S – площадь поперечного сечения соленоида.

· dF = I [ dℓ B ] или F_A = B I 𝓁 sinα з акон Ампера, где F_A – сила Ампера; В – индукция магнитного поля; I – сила тока в проводнике; 𝓁 – длина проводника, α – угол между проводником (направлением тока) и вектором B.

· dF = (µ_oµ I ₁ I ₂ d 𝓁 / 2π a), или F = µ_oµ I ₁ I ₂𝓁 / 2π a – сила взаимодействия прямолинейных параллельных бесконечно длинных токов, где I ₁ и I ₂– сила тока в проводниках; ℓ − длина участка провода, на которой действует сила F; а – расстояние между проводниками.

· A = (µ₀µ I ₁ I ₂ ln (a₂/a₁)) /2π– работа (на единицу длины проводников), необходимая для увеличения расстояния между двумя параллельными бесконечными проводниками. Ток течёт в одном направлении.

· р_m = I S n – магнитный момент контура с током, где S – площадь контура.

· M = [ р_m В ] или M = p_m B sinα – вращательныймомент сил, действующих на плоский контур с током, помещённый в однородное магнитное поле, где М – модуль момента сил; р_m – магнитный момент контура с током; В – модуль индукции магнитного поля; α – угол между вектором индукции магнитного поля и вектором магнитного момента.

· П = (р_m В) или П =р_m В cosα – потенциальная энергия (механическая) контура с током в магнитном поле.

· dA = Id Ф – работа по перемещению проводника с током в магнитном поле, где d Ф – магнитный поток, пересечённый движущимся проводником.

· dA = Id Ф, A = I ∆Ф– работа по перемещению замкнутого контура с током в магнитном поле, d Ф– изменение магнитного потока, сцепленного с контуром.

· ε _i = – d Ф /dt – закон электромагнитной индукции (закон Фарадея),

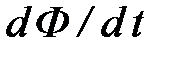− скорость изменения магнитного потока.

· ε _i = B 𝓁 υ sinα – ЭДС индукции в движущихся проводниках, где 𝓁 – длина проводника; α – угол между векторами υ и B; υ – скорость.

· q = ΔФ/ R, или q = N ΔФ/ R = Δ ψ/ R – заряд, протекающий по замкнутому контуру с сопротивлением R при изменении магнитного потока, пронизывающего этот контур.

· ε _i = – d Ф/ dt = B S sin(ωt), ε _i = ε₀ sin(ωt) – ЭДС индукции, возникающая при вращении рамки площадью S с угловой скоростью 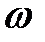в однородном магнитном поле.

· W_m = LI² /2 = µ₀µ N ² S I ²/2 l – энергия однородного магнитного поля внутри длинного соленоида, где I − сила тока, L − индуктивность проводника, по которому течет ток.

· ω_m = B ²/2 µ₀µ = BH/ 2 = µ₀µ H ² / 2 – объемная плотность энергии магнитного поля, где В − индукция магнитного поля, Н − напряженность магнитного поля.

Магнитное поле катушки

· Ф = BS – магнитный поток, где B = const.

· R _м = 𝓁/ – магнитное сопротивление.

· H = B / – напряженность магнитного поля.

· H 𝓁 ~ IN – магнитное напряжение (H 𝓁).

· L = Ф N/I – индуктивность (L = N ² S /𝓁).

· Диамагнетики: – 1 < x < 0; |x| ~10^–5; B' = ~0 → B = x – магнитная восприимчивость.

· Парамагнетики: 0 < x < 1; x ~ 10^–4; B'= ~ 0 → B = .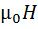

· Ферромагнетики: 10³ –10⁴; B' = ≠ 0 → B = B ₀ +

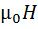· H = + = 1 + x.

· – связь между векторами Jи H.

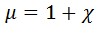· – связь между магнитной проницаемостью среды µ и магнитной восприимчивостью вещества .

· W = Ф I/ 2 = LI ²/2 – энергия магнитного поля катушки.

· ω = W/V = LI ² / 2 V = H ² / 2 = BH/ 2 = B ² / 2 – плотность энергии магнитного поля внутри катушки.

· L = L ₁ + L ₂ – индуктивность двух индуктивно не связанных катушек.

· L = L ₁ + L ₂ ± – индуктивность индуктивно связанных катушек.

· 1/L = 1/L ₁ + 1/L ₂– параллельное соединение двух индуктивно не связанных катушек.

· Трансформатор – устройство, преобразующее переменный ток одного напряжения в переменный ток другого напряжения. Потери Ф → 0. Примем S ₁ = S ₂, = 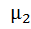, Ф₁ = Ф₂, B ₁ = B ₂, H ₁ = H ₂.

· · – акон полного тока для магнитного поля в веществе (теорема о циркуляции вектора B).

По закону полного тока H 𝓁 = I ₁ N ₁ ; H 𝓁 = I ₂ N ₂→ I ₁ N ₁ = I ₂ ^↑N ₂ ^↓ – трансформатор понижающий (для сварки).

· I ₁ N ₁ = I ₂ ^↓N ₂ ^↑ – трансформатор для передачи энергии на расстояние.

· Трансформатор на холостом ходу P = I ₁ U ₁= I ₂ U ₂; U ₁ N ₂= U ₂ N ₁.

· ε _s = – d ψ /dt = – d(LI)/dt – индукционная ЭДС, где ε _s – мгновенное значение индукционной ЭДС, ψ − потокосцепление, d ψ /dt − производная потокосцепления по времени.

· < ε _s > = Δψ/Δ t – среднее значение индукционной ЭДС, где < ε > − среднее значение индукционной ЭДС, Δψ − изменение потокосцепле­ния, − промежуток времени, в течение которого происходит потокосцепление.

· ε _s = – LdI/dt – ЭДС самоиндукции, где ε _s − мгновенное значение ЭДС самоиндукции, L − индуктивность, dI/dt − ско­рость изменения силы тока в контуре (производная силы тока по времени).

· < ε _s> = L Δ I /Δt – среднее значение ЭДС самоиндукции, где L − индуктивность контура, − изменение силы тока за промежуток времени .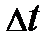

· I = I ₀ e ^{– t/τ}; I = I ₀ (1 − e ^{– t/τ})– токи при размыкании и при замыкании цепи, где τ = L/R− время релаксации (L – индуктивность, R − сопротивление), время, в течение которого значение тока уменьшается в e раз (e = 2,72).

Сила Лоренца

Постоянное однородное магнитное поле.

· F = q [ υB ], F = qυB sinα – сила Лоренца. Сила, действующая на заряд q, движущийся в магнитном поле со скоростью υ.

· R = υ/ ( B), T = 2π / ( B), ν = 1 /T,ω = B – радиус, период, частота, циклическая частота движения заряженной частицы. Скорость υ перпендикулярна индукции В. Период вращения частицы не зависит от её скорости (при υ << c). − удельный заряд частицы.

· h = υ cosα T – шаг винтовой линии.

· – нормальное ускорение.

· Постоянное однородное электрическое и магнитное поля одного направления.

· F = q E + q [ υB ]; – формула Лоренца, где F – результирующая сила, действующая на движущийся заряд q, если на него действует электрическое поле напряжённостью E и магнитное поле индукцией В.

· ускорение заряженной частицы.

· = 2π² mE ²/ B ² – изменение кинетической энергии частицы за время Т.

· π m E / B изменение импульса частицы за время Т.