Замена переменных в тройном интеграле (общий случай).
Замена переменных в тройном интеграле.
16.2.5.1. Теорема о за мена переменных в тройном интеграле. Пусть в пространстве Ouvw задана область G, и пусть отображение преобразует эту область в область V пространства Oxyz. Будем считать, что отображение F задаётся функциями. Пусть: 1). F взаимно однозначно отображает G на V;2). Функции x (u,v,w), y (u,v,w), z(u,v,w) непрерывно дифференцируемы на G (имеют непрерывные частные производные); 3). Якобиан не обращается в нуль на G. Тогда.
Доказательство этой теоремы аналогично доказательству теоремы о замене переменных в двойном интеграле.
Рассмотрим наиболее часто употребляемые криволинейные системы координат в пространстве - цилиндрические и сферические.
При вычислении тройного интеграла, как и двойного, часто удобно сделать замену переменных. Это позволяет упростить вид области интегрирования или подынтегральное выражение.
Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:
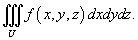
Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:

Предполагается, что выполнены следующие условия:
1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w), равный
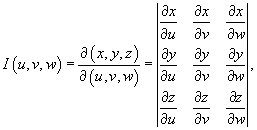
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Тогда формула замены переменных в тройном интеграле записывается в виде:

В приведенном выражении  означает абсолютное значение якобиана.
означает абсолютное значение якобиана.
Для вычисления тройных интегралов часто используются цилиндрические и сферические координаты. Эти случаи рассматриваются подробно на страницах
- Тройные интегралы в цилиндрических координатах
- Тройные интегралы в сферических координатах
Ниже приводятся примеры вычисления интегралов с использованием других преобразований координат.
Тройной интеграл в цилиндрических координатах.
Пусть задана область V Ì XOYZ, ограниченная замкнутой поверхностью; в области V и на ее границе задана функция f (x, y, z).
Тройным интегралом от функции f(x, y, z ) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):
 здесь n – это количество элементарных частей разбиения области V;
здесь n – это количество элементарных частей разбиения области V;
Pi (xi, yi, zi) – произвольно выбранная точка на каждой элементарной части,
i = 1,..., n;
 — ранг разбиения;
— ранг разбиения;
 – диаметр i -ой элементарной части.
– диаметр i -ой элементарной части.

Достаточное условие существования тройного интеграла
Если функция f (x, y, z) непрерывная в замкнутой области V, то 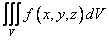 существует.
существует.
Цилиндрические координаты точки в пространствеXOYZ — это ее полярные координаты  в плоскости XOY и координата z.
в плоскости XOY и координата z.
Связь между декартовыми и цилиндрическими координатами:
 Границы изменения цилиндрических координат для всех точек пространства:
Границы изменения цилиндрических координат для всех точек пространства:
 или или 
|

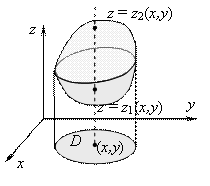

Перевод тройного интеграла к цилиндрическим координатам и сведение его к повторному трехкратному интегралу осуществляется следующими действиями:
 объем V, правильный в направлении оси OZ, проектируется в область
объем V, правильный в направлении оси OZ, проектируется в область  и записывается системой неравенств:
и записывается системой неравенств:
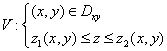 ;
;
 далее область
далее область  записывается неравенствами в полярной системе координат (Рис. 7) и составляется бесконечно малый элемент плоской области в полярных координатах:
записывается неравенствами в полярной системе координат (Рис. 7) и составляется бесконечно малый элемент плоской области в полярных координатах:
 ,
,  ;
;
 в подынтегральной функции и в пределах интегрирования по z делается переход к переменным
в подынтегральной функции и в пределах интегрирования по z делается переход к переменным  и
и 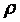 :
:


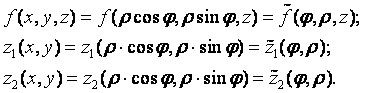
Если выполнить все указанные подстановки, то получится формула вычисления тройного интеграла в цилиндрических координатах:

| (2) |
Таким образом, бесконечно 
Пример 2 (вычисление тройного интеграла в цилиндрических координатах):
Вычислить  , если область V ограничена поверхностями
, если область V ограничена поверхностями
 .
.
Решение
Строим область V и записываем её системой неравенств в цилиндрических
координатах:
 Теперь сводим тройной интеграл к
трехкратному в соответствии с системой
неравенств и вычисляем его:
Теперь сводим тройной интеграл к
трехкратному в соответствии с системой
неравенств и вычисляем его:
  
   .
142.Тройной интеграл в сферических координатах.
Сферические координаты точки М пространства XOYZ определяются следующим образом (Рис. 8): .
142.Тройной интеграл в сферических координатах.
Сферические координаты точки М пространства XOYZ определяются следующим образом (Рис. 8):
j — угол между положительным направлением оси OX и проекцией радиус-вектора Границы изменения сферических координат для всех точек пространства:
Связь сферических и декартовых координат (выводится геометрически):
Замена переменных в тройном интеграле осуществляется в общем случае по формуле, аналогичной формуле замены переменных в двойном интеграле. В частности, при переходе к сферическим координатам эта формула имеет вид: I — это функциональный определитель Якоби третьего порядка:
Таким образом,
Бесконечно малый элемент объема в сферических координатах имеет вид: формула перевода тройного интеграла к сферическим координатам имеет вид:
Далее тройной интеграл сводится к трехкратному в соответствии с неравенствами для области V в сферических координатах. Эффективно переводить в сферические координаты тройной интеграл по областям, в границах которых есть сфера.
Пример 3 (вычисление тройного интеграла в сферических координатах):
Вычислить
Переводим данный тройной интеграл в сферические координаты по формуле (3) и сводим его к трехкратному интегралу в соответствии с системой неравенств:
143.Моменты инерции тела V с плотностью r(x, y, z) относительно осей координат и относительно начала координат.
МОМЕНТОМ ИНЕРЦИИ I тела относительно точки, оси или плоскости называется сумма произведений массы точек тела mi, на квадраты их расстояний ri до точки, оси или плоскости:
Момент инерции тела относительно оси является мерой инерции тела во вращательном движении вокруг этой оси. Момент инерции тела может быть также выражен через массу М тела и его радиус инерции r:
|
 и положительным направлением оси OZ;
и положительным направлением оси OZ;

 или
или  ,
, 



 ,
,



 , так как
, так как  поэтому
поэтому 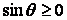 .
. .
. ;
;
 , где
, где 
 представляет собой верхнюю половину шара радиуса 2 с центром в начале координат. Запишем неравенствами область V в сферических координатах:
представляет собой верхнюю половину шара радиуса 2 с центром в начале координат. Запишем неравенствами область V в сферических координатах: 




