В формуле полной вероятности событие А является следствием одного из событий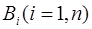 
. События 
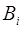обязательно должны
являться единственно возможными и независимыми
+образовывать полную группу событий
являться несовместными и равновозможными
являться несовместными и независимыми
В формуле Байеса событие А является следствием одного из событий 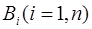. События 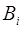обязательно должны
являться единственно возможными и независимыми
+образовывать полную группу событий
являться несовместными и равновозможными
являться несовместными и независимыми
События образуют полную группу событий, если являются
независимыми
единственно возможными и независимыми
+несовместными и единственно возможными
несовместными и равновозможными
Обязательным условием применения формулы 
является
независимость события А и В
события А и В единственно возможны
события А и В противоположны
+совместность событий А и В
Обязательным условием применения формулы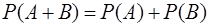 
является
независимость события А и В
+несовместность событий А и В
события А и В единственно возможны
совместность событий А и В
Обязательным условием применения формулы 
является
противоположность событий А и В
+независимость событий А и В
несовместность событий А и В
зависимость событий А и В
Два события называются противоположными, если они
независимы
не совместны
единственно возможны
+образуют полную группу событий
Суммой событий А и В называется событие С, которое происходит, если происходят
только событие А
только событие В
+одно из событий А или В
оба события А и В
Произведением событий А и В называется событие С, которое происходит, если происходит
|
|
только событие А
только событие В
одно из событий А или В
+ оба события А и В
это
вероятность события А при условии, что А и В противоположные события
вероятность события А при условии, что А и В несовместные события
+ вероятность события А при условии, что событие В произошло
произведение событий А и В
Пусть 
. Вероятность появления хотя бы одного из событий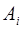 
равна
+ 
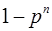
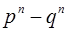
Если некоторый объект А может быть выбран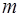 
способами, после чего объект В может быть выбран 
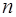способами, то число вариантов выбора пары А и В
равно
+ 
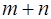
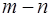
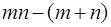
Если некоторый объект А можно выбрать 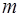способами, а объект В 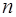способами, то число вариантов отбора или А, или В равно
+
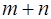
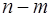
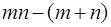
Формула полной вероятности имеет вид
+ 
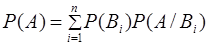
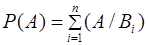
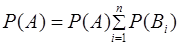
Вероятность невозможного события равна
+0
Вероятность достоверного события равна
+1
Вероятность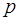 
любого события принадлежит отрезку
+ 
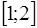
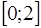
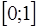
Сумма вероятностей событий, образующих полную группу, равна
1/2
+1
Достоверным называется событие, которое
может произойти, а может не произойти
никогда не произойдет
+обязательно произойдет
происходит три раза
Невозможным называется событие, которое
может произойти, а может не произойти
+никогда не произойдет
обязательно произойдет
происходит три раза
Произведено 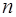испытаний. Событие А произошло 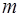раз. Относительная частота события А равна
+ 
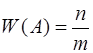
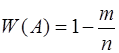
Случайным называется событие А, которое
+может произойти, а может не произойти
никогда не произойдет
обязательно произойдет
|
|
произойдет только совместно с событием 
События А и В называются зависимыми, если
сумма их вероятностей обязательно равна 1
вероятности событий А и В не зависят друг от друга
+вероятность наступления одного из событий зависит от появления или не появления другого
они происходят одновременно
События А и В называются несовместными, если
вероятность наступления одного из событий зависит от появления или не появления другого
+появление одного из них исключает появление другого
сумма их вероятностей никогда не равна 1
если одновременно они могут появиться только конечное число раз
Если вероятность события А равна 0,7, то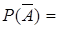 
0,8
0,5
0,4
+0,3
События называются единственно возможными, если они
независимы
несовместны
достоверны
+ одно из них обязательно происходит
Полная группа событий называется пространством элементарных событий, если события
независимы
единственно возможны
+равновозможны
попарно противоположны
Рассматривается пространство из N элементарных событий. Событию А благоприятствуют M элементарных событий. Классическая вероятность события А равна
+ 
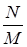
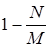
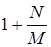
Рассматривается пространство элементарных событий. Некоторое элементарное событие благоприятствует событию А, если
они несовместны
они противоположны
они независимы
+А − следствие этого элементарного события
Если вероятность события А равна нулю, то оно называется
достоверным
случайным
произвольным
+невозможным
Если вероятность события А равна 1, то оно называется
|
|
произвольным
+достоверным
невозможным
случайным
Какая пара событий состоит из противоположных событий
день, ночь
+попадание, промах
черное, белое
большой, маленький
Если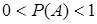 
, то событие А является
невозможным
достоверным
единственно возможным
+случайным
Уровнем значимости называется
значительная вероятность
вероятность близкая к 1
+вероятность, близкая к 0
значительный уровень события
На склад поступает продукция трех цехов. Доли цехов соответственно равны: 1) 30%; 2) 50%; 3) 20%. Процент брака в продукции первого цеха 4%, второго цеха 6%, третьего – 8%. Полная вероятность того, что случайно взятое на складе изделие – бракованное, равна
0,025
+0,058
0,03
0,045
Вероятность того, что размер изделия не соответствует стандарту, равна 0,7. Вероятность того, что вес изделия не соответствует стандарту, равна 0,6. Вероятность, что изделие не стандартно, равна
0,8
0,62
+0,88
0,53
Вероятность того, что студент Иванов сдаст сессию на «отлично», равна 0,7. Вероятность, что студент Петров сдаст сессию на «отлично», равна 0,6. Вероятность, что оба студента станут отличниками, равна
0,51
+0,42
0,24
0,31
Вероятность того, что первый стрелок поразит мишень, равна 0,6, второй 0,5. Вероятность, что хотя бы один из стрелков поразит мишень, равна
0,4
+0,8
0,7
0,5
. 
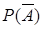равна
0,7
0,4
+0,2
0,5
Вероятность наступления каждого из трех событий p=0,8. Вероятность наступления хотя бы одного из них равна
0,995
+0,992
0,904
0,97
Число сочетаний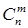 
равно
+ 
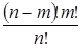
В формуле полной вероятности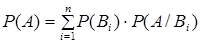 
гипотезы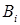 
зависимы
равновозможны
+образуют полную группу событий
достоверные
Вероятность извлечь спелый помидор из корзины равна 0,3. Вероятность, что из двух извлеченных помидоров хотя бы один спелый, равна
0,7
+0,91
0,6
0,09
В формуле полной вероятности 
сумма 
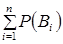равна
1/n
0,7
+1
Система контроля изделий состоит из двух независимых проверок. Вероятность не пройти первую проверку равна 0,4, вероятность не пройти вторую - 0,8. Вероятность, что изделие не пройдет систему контроля, равна
+0,88
0,32
0,12
0,4
Система контроля изделий состоит из двух независимых проверок. Вероятность, что изделие пройдет первую проверку, равна 0,6, вероятность, что изделие пройдет вторую – 0,7. Вероятность, что изделие пройдет систему контроля, равна
0,51
0,73
+0,42
0,24
Три цеха работают на общий склад. (На склад поступает продукция только из этих цехов). Доля изделий первого цеха равна 1/3, второго цеха – 1/4, третьего цеха 7/12. Доля брака среди изделий первого цеха равна 4%, второго – 7%, третьего – 3%. Вероятность брака на складе равна
5%
8,5%
+6,5%
3%
В корзине 5 красных и 8 зеленых яблок. Извлекается одно яблоко и съедается. Вероятность второй раз извлечь красное яблоко, если в первый раз извлечено красное, равна
+ 
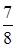
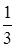
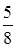
В корзине 3 сладких и 5 кислых яблок. Извлекается одно яблоко и съедается. Затем извлекается второе яблоко. Вероятность, что первый раз извлечено кислое яблоко, а второй раз – сладкое равна
+ 
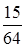
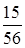
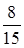
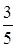
В группе 20 студентов. Из них 8 девушек и 12 юношей. Преподаватель проводит опрос. Опрошенный студент больше не вызывается. Вероятность, что первый раз будет вызвана девушка, а второй – юноша, равна
+ 
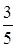
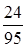
Вероятность наступления каждого из двух событий равна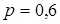 
. Вероятность наступления хотя бы одного из них равна
0,52
+0,64
0,83
0,36
В урне 10 шаров. Из них два черных, а остальные белые. Наудачу взято 2 шара. Вероятность, что они оба черные равна
+ 
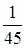
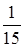
Брошены 2 игральные кости. Вероятность, что сумма очков равна 7, есть
+ 
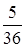
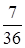
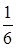
Осенью в речной порт Казани приходят пассажирские суда только из трех городов: Нижнего Новгорода, Москвы и Самары. Вероятность прибытия из Москвы равна 0,1, из Нижнего Новгорода 0,6. Вероятность прибытия из Самары равна
0,2
0,5
0,4
+0,3
Вероятность, что механик найдет неисправность в двигателе самолета, равна 0,6. Вероятность, что механик найдет неполадки в шасси, равна 0,7. Вероятность, что самолет не годен к эксплуатации, равна
0,58
0,42
+0,88
0,12