PB= ρgVтд,
где Vтд – объем «тела давления», образованного криволинейной поверхностью, ее проекцией на пьезометрическую поверхность, и соединяющими их вертикальными образующими
Линия действия вертикальной составляющей РB силы давления проходит через центр тяжести «тела давления». Вертикальная сила давления РB направлена вверх, если этот объем «тела давления» строится со стороны несмоченной части стенки, и вниз - если объем этого тела строится со стороны смоченной части стенки.
Объемы некоторых фигур и положения их центров тяжести приведены в таблице.
20. Относительный покой жидкости
Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.
Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляется новая — сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.
Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.
|
|
Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g сила инерции а (рисунок 2.9). Равнодействующая этих двух сил
(2.12)
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой всегда составляет 90°. Изгеометрических соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения
tga = а/g.
Для определения давления в произвольно выбранной точке на расстоянии l от свободной поверхности используется математическая зависимость
p = p0 + l ρ j. (2.13)
Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.
|
Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а= 0 из (2.12) следует j = g. Тогда c учетом l = h из (2.13) получим формулу (2.1), т.е. основное уравнение гидростатики
. 
Другим случаем относительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, расположенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω 2 r. Равнодействующая этих двух сил
определяет положение свободной поверхности жидкости. Но в рассматриваемом случае центробежное ускорение является переменной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую форму и описывается уравнением
|
|
,
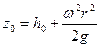где z0 — высота расположения точки свободной поверхности относительно дна сосуда;
h 0 — высота жидкости на оси вращения.
Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразделе 2.1. Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:
. (2.14)
На практике часто встречается другой частный случай — вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:
. (2.15)
21. Основы кинематики и динамики жидкости. Основные понятия
Кинематика жидкости отличается от кинематики твердого тела, у которого все точки жестко соединены между собой. В жидкости частицы могут перемещаться относительно друг друга. Задачей кинематики жидкости является определение скорости в любой ее точке, то есть определение поля скоростей.
В гидравлике существуют понятия идеальной и реальной жидкости. Идеальной жидкостью называют абстрактную модель жидкости, абсолютно лишенной вязкости и несжимаемой. Реальная жидкость всегда рассматривается как вязкая, а сжимаемостью часто пренебрегают.
|
|
Рассмотрим движение идеальной жидкости. В такой жидкости, как и в неподвижной, возможны тоже только сжимающие нормальные напряжения, то есть гидромеханическое давление. Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости: на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой другой точке – по всем направлениям одинаково.
Течение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным).
Установившимсяназывается течение, неизменное во времени, при котором давление и скорость являются только функциями координат, но не зависят от времени. Давление и скорость могут изменяться при перемещении частицы жидкости, но в данной неподвижной относительно русла точке давление и скорость во времени не изменяются:
В частном случае стационарное течение жидкости может быть равномерным, когда скорость каждой частицы не изменяется при изменении ее координат, и поле скоростей остается неизменным вдоль потока.
Неустановившимсяназывается течение жидкости, все характеристики которого (или некоторые из них) изменяются во времени в точках рассматриваемого пространства:
Исследовать установившиеся течения значительно проще, чем неустановившиеся. В дальнейшем мы будем чаще всего вести речь об установившихся течениях. Траектории частиц при стационарном течении неизменны во времени. При нестационарном течении траектории частиц, проходящих через данную точку пространства в различные моменты времени, могут иметь различную форму. Поэтому для рассмотрения картины течения вводится понятие линии тока.
Рис. 16. Линия тока
Линия тока (Рис. 16) – это кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.
Рис. 17. Трубка тока
Если в движущейся жидкости взять бесконечно малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока (Рис. 17). Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.
В любой точке трубки тока скорости частиц жидкости направлены по касательной, нормальная к этой поверхности составляющая скорости отсутствует, следовательно, при установившемся движении ни одна частица жидкости ни в одной точке не может проникнуть внутрь струйки или выйти наружу. Таким образом, трубка тока является как бы непроницаемой стенкой, а элементарная струйка – это самостоятельный элементарный поток.
Живым сечением потока называется поверхность в пределах потока, проведенная нормально к линиям тока. Если элементарные струйки проходят параллельно, то живое сечение потока будет плоским.
Смоченным периметром h называют длину линии соприкосновения жидкости с твердыми стенками в данном живом сечении.
Гидравлическим радиусом называют отношение площади живого сечения потока к смоченному периметру:
.
Гидравлический диаметр равен 4 гидравлическим радиусам:
Dг = 4Rг.
Легко убедиться, что для круглого сечения R г = 0,5 R, а D г = D.
Чаще всего живое сечение имеет форму круга, но если форма сечения иная, то в формулы подставляют эквивалентный гидравлический диаметр.
Различают напорное и безнапорноетечение. Напорным называют течение в закрытых руслах без свободной поверхности, а безнапорным – течение со свободной поверхностью. При напорном течении давление обычно вдоль потока переменное, при безнапорном – постоянное (на свободной поверхности) и чаще всего атмосферное.
22. Расход. Уравнение расхода.
Расход жидкости – количество жидкости, протекающей в единицу времени через живое сечение потока.
Различают объёмный, массовый и весовой расходы жидкости.
Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, л/с. Он вычисляется по формуле
где Q - объёмный расход жидкости,
V - объём жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле
где Q M - массовый расход жидкости,
M -масса жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, кН/с. Формула для его определения выглядит так:
где Q G - весовой расход жидкости,
G - вес жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.
Расход элементарной струйки – объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Таким образом:
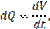
Если последнее выражение проинтегрировать по площади живого сечения потока можно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек
Применение этой формулы в расчетах затруднительно, так как расходы элементарных струек жидкости в разлчных точках живого сечения потока различны. Поэтому чаще используют среднюю скорость потока 
.
Уравнения объемного расхода во всех сечениях элементарной струйки
Аналогичные уравнения можно составить и для потока конечных размеров
Это уравнения неразрывности потока капельной жидкости.
23. Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и 2-2. Площади живых сечений потока обозначим dS1 и dS2. Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0-0 характеризуется величинами Z1 и Z2. Давления и скорости жидкости в этих сечениях имеют значения P1, P2 и v1, v2 соответственно.
Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.
За малый промежуток времени dt частицы жидкости из 1-1 переместятся в 1'-1' на расстояние, равное v1dt, а частицы из 2-2 в 2' - 2' на расстояние v2dt.
Согласно теореме кинетической энергии приращение энергии тела (в данном случае выделенного объёма жидкости) равно сумме работ всех действующих на него сил.
Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести. Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки. Она будет равна произведению силы P1dS1 на путь v1dt:
Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение
Полная работа, выполненная силами давления, примет вид:
Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их веса dG:
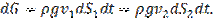
При перетекании от сечения 1-1 в сечение 2-2 центр тяжести выделенного объёма переместится на разность высот (Z1–Z2) и работа, произведённая силами тяжести, составит:
Проанализируем теперь изменение кинетической энергии рассматриваемого объёма элементарной струйки жидкости.
Приращение кинетической энергии выделенного объёма за dt равно разности его кинетических энергий в сечениях 1-1 и 2-2. Это приращение составит
Приравнивая приращение кинетической энергии к сумме работ сил тяжести и сил давления, придём к виду:
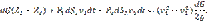
Разделив обе части на вес dG, т.е. приведя уравнение к единичному весу, получим
После сокращения и преобразований придём к искомому виду
Таким образом, получено уравнение Бернулли для элементарной струйки невязкой жидкости при установившемся движении под действием сил тяжести.
24. В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. Поэтому в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора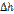 
составят:
где H1-1 ‑ напор в первом сечении потока жидкости,
H2-2 ‑ напор во втором сечении потока,
h ‑ потерянный напор ‑ энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть
Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.
Если учесть, что характеристики потока V и 
зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока.
Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём
Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор 
а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.