Если гидравлический уклон всегда положителен, то пьезометрический может быть и положительным, и отрицательным. Следовательно, пьезометрическая линия параллельна энергетической, и пьезометрический уклон равен гидравлическому.
Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, называют геометрическим уклоном i и определяют по формуле
где l ‑ расстояние между сечениями потока.
25. При изучении движения реальных жидкостей встречается много. Первым этапом изучения процесса является отбор определяющих этот процесс факторов и исключение из рассмотрения тех из них, которые оказывают пренебрежимо малое влияние.
Гидродинамическое подобие складывается из трех составляющих: геометрического, кинематического и динамического подобия.
Геометрическое подобие, как известно из геометрии, предполагает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие тех поверхностей, которые ограничивают потоки, то есть подобие русел или каналов. При этом подобными должны быть не только русла в пределах изучаемого участка, но и непосредственно перед и за ними, так как они будут оказывать влияние на характер течения жидкости на изучаемом участке. Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим через kL. Эта величина одинакова (idem) для подобных русел I и II:
.
Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей:
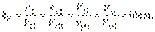
где kV – масштаб скоростей, одинаковый при кинематическом подобии.
Так как
где T – время, kT – масштаб времени.
Очевидно, что для кинематического подобия необходимо геометрическое подобие русел.
Динамическое подобие – это пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил.
В потоках жидкости обычно действуют разные силы: силы давления, вязкости, тяжести и др. Соблюдение этих пропорциональностей означает полное гидродинамическое подобие. Осуществить полное подобие на практике удается далеко не всегда, поэтому часто имеют дело с частичным (неполным) подобием, при котором пропорциональны только лишь основные, главные силы.
Для напорных течений в закрытых руслах, то есть для потоков в трубах, в гидромашинах и т. п., такими силами являются силы давления, вязкости и инерции. На жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление: p пр = p + grh, то есть она учитывается.
Силы инерции определяются произведением массы на ускорение F = ma, а их отношение в подобных потоках равно масштабу сил:
где k r – масштаб плотностей.
Таким образом, силы инерции пропорциональны плотности, квадрату скорости и размеру L во второй степени, то есть площади S:
Силы инерции примем за основу и другие силы будем сравнивать с инерционными, то есть с 
Таким образом, для гидродинамического подобия потоков необходимо, чтобы
Это отношение называют числом Ньютона и обозначают Ne
Рассмотрим три характерных случая воздействия на движущуюся жидкость основных сил и найдем условия подобия потоков.
1. На жидкость действуют лишь силы давления и инерции. Тогда F = D pS ~ D pL2 и условие гидродинамического подобия примет вид:
где D p – разность давлений или просто давление,
Eu – безразмерный критерий, число Эйлера.
Таким образом, в этом случае условием гидродинамического подобия потоков является равенство чисел Эйлера, которые равны величине, пропорциональной отношению сил давления к силам инерции.
2. На жидкость действуют силы вязкости, давления и инерции. Тогда 
. Условие гидродинамического подобия потоков после деления на r V 2 L 2 примет вид:
где Re – безразмерный критерий, называемый числом Рейнольдса.
Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Рейнольдса, подсчитанных для сходственных сечений потоков.
3. На жидкость действуют силы тяжести, давления и инерции. Тогда F ~ g r L 3 и условие гидродинамического подобия потоков примет вид:
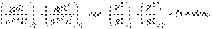
где Fr – безразмерный критерий, число Фруда.
Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Фруда.
26. Опыты показывают, что возможны два режима или два вида течения жидкостей и газов в трубах: ламинарный и турбулентный.
ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления. При таком течении все линии тока определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т. е. прямолинейно; отсутствуют поперечные перемещения жидкости.
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объемов жидкости.
Режим течения данной жидкости в данной трубе изменяется при вполне определенной средней по сечению скорости течения υ кр, которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости v и обратно пропорционально диаметру d трубы, т. с.
.
Входящий в эту формулу безразмерный коэффициент пропорциональности k одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и вязкостью v:
k = υкр d/v.
Полученное безразмерное число называется критическим числом Рейнольдса и обозначается
Reкр = υкр d/v. (3.19)
Критическое число Рейнольдса Reкр не зависит от рода жидкости и размеров сечения, а лишь в небольшой степени определяется формой сечения и шероховатостью стенок трубы.
Таким образом, критическое число Рейнольдса является критерием, определяющим режим течения в трубах.
Как показывают опыты, для труб круглого сечения Reкр ≈ 2300.
Зная скорость движения жидкости, ее вязкость и диаметр трубы, можно расчетным путем найти число Re и, сравнив его с Reкр, определить режим течения жидкости.
При Re < Reкр течение является ламинарным, при Re > Reкр — турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при
Re ≥ 10000, а при Re = 2300 … 10000 имеет место переходная, критическая область.
На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно происходит в водопроводах, а также в трубах, по которым перетекают бензин, керосин, спирты, кислоты и другие маловязкие жидкости.
27. В некоторых случаях при движении жидкости в закрытых руслах происходят явления, связанные с изменением агрегатного состояния жидкости, т.е. с превращением ее в пар, а также с выделением из жидкости растворенных в ней газов. Например, при течении жидкости через местное сужение трубы увеличивается скорость и падает давление. Если абсолютное давление при этом достигает значения, равного давлению насыщенных паров этой жидкости при данной температуре, или давлению, при котором начинается выделение из нее растворенных газов, то в данном месте потока начинается интенсивное парообразование (кипение) и выделение газов. В расширяющейся части скорость потока уменьшается, а давление возрастает, и выделение паров и газов прекращается; выделившиеся пары конденсируются, а газы постепенно вновь растворяются. Это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке, называется кавитацией.
Вода или иная жидкость под давлением в несколько атмосфер подводится к регулировочному крану (вентилю) А и далее протекает через прозрачную трубку Вентури, которая сначала плавно сужает поток, затем еще более плавно расширяет и через кран Б выводит в атмосферу.
При небольшом открытии регулировочного крана и, следовательно, при малых значениях расхода и скорости жидкости падение давления в узком месте трубки незначительно, поток вполне прозрачен, и кавитация отсутствует. При постепенном открытии крана происходит увеличение скорости жидкости в трубке и падение абсолютного давления.
При некотором значении этого давления, которое можно считать равным давлению насыщенных паров (р абс2 = р н.п), в узком месте трубки появляется отчетливо видимая зона кавитации, представляющая собой область местного кипения жидкости и последующей конденсации паров. Размеры зоны кавитации возрастают по мере дальнейшего открытия крана, т. е. при увеличении давления в сечении 1-1, а следовательно, и расхода. Однако как бы при этом ни возрастал расход, давление в узком сечении 2-2 сохраняется строго постоянным потому, что постоянно давление насыщенных паров.
Кавитация сопровождается характерным шумом, а при длительном ее воздействии также эрозионным разрушением металлических стенок.
При возникновении кавитации значительно увеличивается сопротивление трубопроводов и, следовательно, уменьшается их пропускная способность, потому что каверны уменьшают живые сечения потоков, скорость в которых резко возрастает, и, как следствие, резко возрастает коэффициент местных сопротивлений.
В гидросистемах кавитация может возникать в трубопроводах низкого давления — во всасывающих трубопроводах.
28. Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода - это линейные потери; в других - они сосредоточены на очень коротких участках, длиной которых можно пренебречь, - на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.
Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.
29. Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастают плавно.
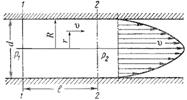
Уравнение, связывающее переменные 
и 
, имеет следующий вид:
где P1 и P2 - давления соответственно в сечениях 1 и 2.
У стенок трубы величина r = R,, значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной
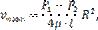
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.
Максимальная скорость дает высоту параболоида
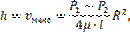
Как известно из геометрии, объем параболоида высотой h и площадью 
равен
а в нашем случае
Если вместо R подставить диаметр трубы d, то
Расход в трубе можно выразить через среднюю скорость:
откуда 
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима.
Потеря давления в трубопроводе будет равна
Если в формуле динамический коэффициент вязкости 
заменить через кинематический коэффициент вязкости и плотность 
(
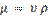) и разделить обе части равенства на удельный вес жидкости 
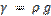, то получим:
Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:
Уравнение может быть преобразовано в универсальную формулу Дарси‑Вейсбаха, которая окончательно записывается так:
где 
- коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:
Однако при ламинарном режиме для определения коэффициента гидравлического трения Т.М. Башта рекомендует при Re < 2320 применять формулу
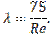
33. Истечение под уровень
При течении жидкости в закрытых руслах часто приходится иметь дело с истечением жидкости не в газовую среду, а в пространство, заполненное этой же жидкостью (рисунок 4.2). Такое истечение называется истечением под уровень или истечением через затопленное отверстие.
Здесь, так же как и в предыдущем случае, при определении расхода Q следует составить уравнение Бернулли. Запишем его для 
сечений 1-1 и 2-2, в которых скорости движения жидкости принимаются равными нулю:
,
где 
— потери напора при движении жидкости между сечениями 1-1 и 2-2.
При определении потерь напора в этом случае необходимо учитывать, что они складываются из двух составляющих:
,
где ho — потери напора на торможение частиц жидкости о входную кромку отверстия;
hв.р — потери напора на внезапное расширение в баке после прохождения жидкости через отверстие.
Потери ho практически равны потерям при истечении через отверстие в газовую среду:
.
Следует иметь в виду, что при истечении под уровень вся кинетическая энергия струи, приобретенная частицами жидкости в отверстии, при попадании в покоящуюся жидкость теряется на вихреобразование так же, как при внезапном расширении. Поэтому потери hв.р численно равны соответствующему скоростному напору, посчитанному по средней скорости жидкости в струе с учетом коэффициента Кориолиса α:
.
Таким образом, суммарные потери напора
.
Подставив полученное выражение в уравнение Бернулли, получим
.
Если в этом уравнении за расчетный напор принять выражение 
, то после преобразований можно получить формулу, определяющую значение средней скорости жидкости в сжатом сечении струи:
,
которая совпадает с формулой (4.2). Это значит, что, проводя дальнейшие преобразования, необходимые для получения формулы, определяющей расход Q при истечении, можно получить формулы (4.6) и (4.7).
Таким образом, как при истечении в газовую среду, так и при истечении под уровень расчетные формулы, определяющие расход Q, имеют один и тот же вид. Кроме того, как показала практика, коэффициенты 
, 
и 
, использующиеся в этих формулах, в обоих случаях истечения имеют одинаковые значения при равенстве соответствующих чисел Рейнольдса.
34. Истечение жидкости через насадки.
Насадками называются короткие трубки, монтируемые, как правило, с внешней стороны резервуара таким образом, чтобы внутренний канал насадка полностью соответствовал размеру отверстия в тонкой стенке. Наличие такой направляющей трубки приведет к увеличению расхода жидкости при прочих равных условиях.
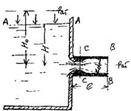
Причины увеличения следующие При отрыве струи от острой кромки отверстия струя попадает в канал насадка, а поскольку струя испытывает сжатие, то стенок насадка она касается на расстоянии от 1,0 до 1,5 его диаметра. Воздух, который первоначально находится в передней части насадка, вследствие неполного заполнения его жидкостью постепенно выносится вместе с потоком жидкости. Таким образом, в этой области образуется «мёртвая зона», давление в которой ниже,
чем давление в окружающей среде (при истечении в атмосферу в «мёртвой зоне» образуется вакуум). За счёт этих факторов увеличивается перепад давления между резервуаром и областью за внешней его стенкой и в насадке генерируется так называемый эффект подсасывания жидкости из резервуара. Однако наличие самого насадка увеличивает гидравлическое сопротивление для струи жидкости, т.к. в самом насадке появляются потери напора по длине трубки. Если трубка имеет ограниченную длину, то влияние подсасывающего эффекта с лихвой компенсирует дополнительные потери напора по длине. Практически эти эффекты (подсасывание и дополнительные сопротивления по длине) компенсируются при соотношении: / = 55 d. По этой причине длина насадков ограничивается / = (3 -5)d. По месту расположения насадки принято делить на внешние и внутренние насадки. Когда насадок монтируется с внешней стороны резервуара (внешний насадок), то он оказывается более технологичным, что придаёт ему преимущество перед внутренними насадками. По форме исполнения насадки подразделяются на цилиндрические и конические, а по форме входа в насадок выделяют ещё коноидальные насадки, вход жидкости в которые выполнен по форме струи.
Внешний цилиндрический насадок. При истечении жидкости из цилиндрического насадка сечение выходящей струи и сечение отверстия одинаковы, а это значит, что коэффициент сжатия струи 
= 1.
Сходящиеся насадки. Если придать насадку форму конуса, сходящемуся по направлению к его выходному отверстию, то такой насадок будет относиться к группе сходящихся конических насадков. Такие насадки характеризуются углом конусности а. От величины этого угла зависят все характеристики насадков. Как коэффициент скорости, так и коэффициент расхода увеличиваются с увеличением угла конусности, при угле
» 
конусности в 13° достигается максимальное значение коэффициента расхода превышающее 0,94. При дальнейшем увеличении угла конусности насадок начинает работать как отверстие в тонкой стенке, при этом коэффициент скорости продолжает увеличиваться, а коэффициент расхода начинает убывать. Это объясняется тем, что уменьшаются потери на расширение струи после её сжатия. Область применения сходящихся насадков связана с теми случаями, когда необходимостью иметь большую выходную скорость струи жидкости при значительном напоре (сопла турбин, гидромониторы, брандспойты).
Расходящиеся насадки. Вакуум в сжатом сечении расходящихся насадков больше, чем у цилиндрических насадков и увеличивается с возрастанием угла конусности, что увеличивает расход жидкости. Но с увеличением угла конусности расходящихся насадков возрастает опасность отрыва струи от стенок насадков. Необходимо отметить, что потери энергии в расходящемся насадке больше, чем в насадках других типов. Область применения расходящихся насадков охватывает те случаи, где требуется большая пропускная способность при малых выходных скоростях жидкости (водоструйные насосы, эжекторы, гидроэлеваторы и др.)
Коноидальные насадки. В коноидальных насадках вход в насадки выполнен по профилю входящей струи. Это обеспечивает уменьшение 
потерь напора до минимума. Так значение коэффициентов скорости и расхода в коноидальных цилиндрических насадков достигает 0,97 - 0,99.