Гидростатика – раздел гидравлики, который изучает законы равновесия жидкости, находящейся в состоянии относительного покоя.
Основным параметром, характеризующим жидкость в таком состоянии, является давление, называемое гидростатическим.
Следует помнить, что в любой гидравлической системе действует абсолютное давление, которое по отношению к атмосферному может быть (см.рис.1):
1.  .
.
2.  , тогда
, тогда 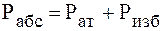 .
.
3.  , тогда
, тогда  .
.
4. 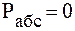 .
.

Рис.1
Гидростатическое давление в любой точке покоящейся жидкости может быть определено из дифференциального уравнения равновесия жидкости (уравнения Эйлера):
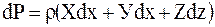 , (1)
, (1)
где r - плотность жидкости; Х, У, Z – алгебраическая сумма проекций ускорений от массовых сил.
Для случая, когда единственной массовой силой, действующей на объем жидкости, является сила тяжести, Х, У = 0, Z = -g; тогда  , или
, или  , т.к.
, т.к.  . Т.е
. Т.е
 (одно и то же). (2)
(одно и то же). (2)

Рис.2
Из иллюстрации выражения 2 (рис.2) следует

 (3)
(3)
Уравнения (2) и (3)являются выражениями основного уравнения гидростатики, позволяющего вычислять гидростатическое давление в любой точке покоящейся жидкости, для чего в каждом конкретном случае составляется уравнение равновесия.
Задача 11
Покоящийся на неподвижном поршне и открытый сверху и снизу сосуд массой m = 16 кг состоит из двух цилиндрических частей, внутренние диаметры которых D = 0,5 м и d = 0,3 м. Определить, какой минимальный объем W воды должен содержаться в верхней части сосуда, чтобы сосуд всплыл над поршнем. Трением сосуда о поршень пренебречь.

Рисунок к задаче 11
Задача 12
Определить, на какой угол повернется кольцевой манометр, имеющий диаметр трубки d = 20 мм и средний диаметр кольца D = 200 мм, если величины давления воздуха, подводимого к ветвям: p1 = 90 кПа, р2 = 80 кПа, вес груза G = 5,25 Н и его плечо относительно оси вращения а = 120 мм.
Указание. Рассмотреть условие равновесия прибора, сводящееся в данном случае к равенству нулю суммы моментов относительно оси вращения сил давления газа и ртути на внутреннюю поверхность кольцевой трубки и веса груза.

Рисунок к задаче 12
Задача 13
Определить абсолютное давление в сосуде по показанию жидкостного манометра, если известно: h1=2 м; h2=0,5 м; h3=0,2 м; rм=880 кг/м3, rрт = 13600 кг/м3, rводы = 1000 кг/м3.


Рисунок к задаче 13
Задача 14
Определить вакуумметрическое давление воды рв в точке В трубопровода, расположенной на а=200 мм ниже линии раздела между водой и ртутью. Разность уровней ртути в коленах манометра h=300 мм, dрт = 13,6.


Рисунок к задаче 14
Задача 15
Определить давление на свободной поверхности воды в резервуаре, если hрт = 200 мм; h = 1,2 м; Z = 1 м; dрт = 13,6.


Рисунок к задаче 15
Задача 16
Для измерения высоты налива нефти в открытом резервуаре установлена вертикальная труба, открытый нижний конец которой почти доходит до днища. В эту трубу с очень малой скоростью подают воздух, что позволяет пренебречь гидравлическими сопротивлениями. Определить высоту Н налива нефти плотностью r = 890 кг/м3, если давление воздуха, поступающего в резервуар, эквивалентно высоте h = 890 мм рт.ст.
 |
Рисунок к задаче 16
Задача 17
Для измерения падения давления в вентиляционной трубе применяется чашечный наклонный микроманометр, наполненный спиртом плотностью r = 0,8 г/см3. Наклон трубки a = 30°. Определить необходимую длину l манометрической шкалы для измерения падения давления Dр = 0,001 атм.

Рисунок к задаче 17
Задача 18
Определить абсолютное давление воздуха в сосуде, если показание ртутного прибора h = 368 мм, высота H = 1 м. Плотность ртути r = 13600 кг/м3. Атмосферное давление 736 мм рт.ст.


Рисунок к задаче 18
Задача 19
Определить абсолютное давление воздуха в баке р1, если при атмосферном давлении hа = 760 мм рт.ст. показание ртутного вакуумметра hрт = 0,2 м, высота h = 1,5 м. Каково при этом показание пружинного вакуумметра? Плотность ртути r = 13600 кг/м3.

Рисунок к задаче 19
Задача 20
Кессон П-образного сечения в начале работ по выемке грунта покоится на дне реки на глубине Н = 20 м от поверхности воды, сильно пропускает воду. Как велико должно быть давление р сжатого воздуха в рабочей камере, для того чтобы вода не просачивалась через речное дно?


Рисунок к задаче 20
3. Сила гидростатического давления
на плоские поверхности

Рис.1
Если плоская поверхность АВ (рис.1) подвергается одностороннему давлению жидкости высотой h и избыточному давлению на ее поверхности Р0 при атмосферном давлении с другой стороны, то результирующая сила Р, воспринимаемая поверхностью и нормальная к ней определяется по формуле
 , (1)
, (1)
где р0+ rghc – давление в центре тяжести смоченной поверхности; w - смоченная площадь поверхности.
Первая составляющая силы Р0 = р0w будет приложена в центре тяжести (точке С), т.к. давление Р0 распределяется равномерно по поверхности и эпюра давления – прямоугольник.
Вторая составляющая от столба жидкости Рh = rghcw будет смещена по отношению точки С и приложена ниже ее в точке d, называемой центром давления, т.к. давление от столба жидкости распределено неравномерно и эпюра от этого давления – прямоугольный треугольник.
Расстояние от свободной поверхности до центра давления определяется из выражения
 , (2)
, (2)
где Jc – момент инерции площади поверхности относительно горизонтальной оси, проходящей через центр тяжести площади этой поверхности.
Например, для прямоугольника  , треугольника
, треугольника  , круга
, круга  и т.д., т.е. Jc зависит от геометрической формы поверхности и ее размеров, она берется из справочной литературы.
и т.д., т.е. Jc зависит от геометрической формы поверхности и ее размеров, она берется из справочной литературы.
Следует помнить, что сила давления на поверхность есть всегда результат действия разности давлений на эту поверхность.
Задача 21
Дроссельный затвор диаметром D = l м, установленный в трубопроводе, может свободно вращаться вокруг горизонтальной центральной оси О-О. Глубина погружения центра тяжести затвора Н =10 м. При закрытом затворе за ним в трубопроводе воды нет.
Определить:
1) момент Мд силы давления воды относительно горизонтальной оси О-О вращения затвора;
2) момент Мтр силы трения, если диаметр цапф d = 200 мм, а коэффициент трения f = 0,2;
3) момент силы, который необходимо приложить для открытия затвора при его вращении по часовой стрелке.

Рисунок к задаче 21
Задача 22
Определить силу давления на плоский прямоугольный затвор и центр давления. Глубина воды в верхнем бьефе h1 = 3 м, в нижнем h2 = 1,2 м. Ширина затвора b = 4 м, высота H = 3,5 м. Расчет произвести аналитическим и графо-аналитическим способами. Найти начальное подъемное усилие, если толщина затвора t = 0,08 м, плотность материала, из которого изготовлен затвор, ρ = 1200 кг/м3, коэффициент трения затвора о пазы f = 0,5.

Рисунок к задаче 22
Задача 23
Плоский затвор, закрывающий выпускное отверстие в плотине, может перемещаться по ее стенке, наклоненной к горизонту под углом а = 70° (отметки уровней даны в метрах). Размеры затвора: высота h = 1,8 м; ширина b == 2,4 м; толщина с = 0,4 м; масса затвора m = 2 т. Определить силу Т, необходимую для начального смещения закрытого затвора вверх, если коэффициент трения скольжения затвора в направляющих f = 0,35.
 |
Рисунок к задаче 23
Задача 24
Щитовой затвор должен автоматически опрокидываться для пропуска воды при уровне последней Н1 = 6 м. Щит поворачивается на цапфах О диаметром d = 0,4 м, имеющих коэффициент трения скольжения f= 0,2. Ширина щита В = 8 м, его угол наклона а = 60°. Найти расстояние х, на каком должна быть расположена ось поворота щита, если под щитом имеется постоянный уровень воды Н2 = 3 м, и определить силу Р, воспринимаемую его опорами в момент опрокидывания.

Рисунок к задаче 24
Задача 25
Прямоугольный поворотный затвор размером L x B = 2x3 м перекрывает выход воды в атмосфepy из резервуара, уровень в котором Н = 4 м.
Определить:
1. На каком расстоянии х от нижней кромки затвора следует расположить его ось поворота, чтобы для открытия затвора нужно было преодолевать только момент трения в цапфах О.
 |
2. Момент трения Мтр, если диаметр цапф d = 150 мм, коэффициент трения скольжения в цапфах f = 0,2.
Рисунок к задаче 25
Задача 26
Поворотный клапан АО закрывает выход из бензохранилища в трубу квадратного сечения со стороной h = 0,3 м. Прямоугольная пластина клапана опирается на срез трубы, сделанный под углом 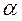 =45°. В трубе жидкость отсутствует.
=45°. В трубе жидкость отсутствует.
 |
Определить (без учета трения в опоре О клапана и ролике В) силу Т натяжения троса, необходимую для закрытия клапана, если уровень бензина Н = 0,85 м, давление над ним по манометру М=5 кПа. Плотность бензина r = 700 кг/м3.
Рисунок к задаче 26
Задача 27
Поворотный клапан закрывает выход из бензохранилища в трубу квадратного сечения. Определить, какую силу Т нужно приложить к тросу для открытия клапана при следующих данных: h = 0,4 м, Н=1,0 м; α = 30°; плотность бензина rб = 700 кг/м3. Манометрическое давление паров бензина в резервуаре рм = 10 кПа.


Рисунок к задаче 27
Задача 28
Труба прямоугольного сечения a×b = 0,5×0,2 м для выпуска нефти из открытого нефтехранилища закрывается откидным плоским клапаном, расположенном под углом а = 60° к горизонту. Определить начальное подъемное усилие Т троса, чтобы открыть клапан при глубине нефти h = 2,8 м. Построить эпюру гидростатического давления на клапан.
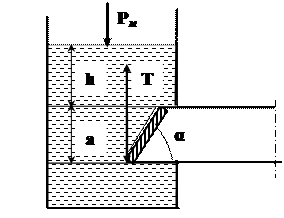
Рисунок к задаче 28
Задача 29
Труба диаметром d = 300 ммдля выпуска нефти из открытого нефтехранилища закрывается откидным клапаном, расположенным под углом a = 45° к горизонту. Определить усилие Р, которое нужно приложить к тросу, чтобы открыть клапан, если глубина расположения клапана Н = 8 м, плотность нефти r = 860 кг/м3.

Рисунок к задаче 29
Задача 30
Наклонный щит плотины имеет возможность поворачиваться около оси О. При каком уровне воды Н щит перевернется, если угол наклона щита a = 60°, расстояние от нижней кромки щита до шарнира а = 0,9 м?
Весом щита и трением в оси пренебречь.

Рисунок к задаче 30
4. Сила гидростатического давления
на криволинейные поверхности

Рис.1
Для криволинейных поверхностей, симметричных относительно вертикальной плоскости (большинство практических задач), сумма элементарных сил давления приводится к одной равнодействующей силе, лежащей в плоскости симметрии, или к паре сил, лежащей в той же плоскости.
Методика определения равнодействующей (результирующей) силы Р (рис.1) сводится к разложению ее на горизонтальную Рх и вертикальную Рz составляющие с их дальнейшим определением.
Горизонтальная составляющая силы давления, воспринимаемой криволинейной поверхностью, равна силе давления на вертикальную проекцию этой поверхности, нормальную к плоскости симметрии, и определяется по формуле
 , (1)
, (1)
где hc – расстояние по вертикали от центра тяжести вертикальной проекции поверхности до пьезометрической плоскости о-о, т.е. до плоскости, где расчетное давление равно атмосферному; wz – площадь вертикальной проекции поверхности; r - плотность жидкости; g – ускорение свободного падения.
Линия действия силы Рх, проходя через центр давления вертикальной проекции поверхности, лежит в плоскости симметрии и смещена относительно центра тяжести вертикальной проекции на расстояние
 ,
,
где Jc – момент инерции площади вертикальной проекции относительно горизонтальной оси, проходящей через центр тяжести проекции.
Вертикальная составляющая силы давления, воспринимаемой криволинейной поверхностью, равна весу жидкости в объеме «тела давления» Wт.д, которое ограничено самой поверхностью, свободной поверхностью и вертикальной проектирующей поверхностью, построенной на контуре криволинейной поверхности. Она определяется по формуле
 . (2)
. (2)
Сила Рz проходит через центр тяжести объема «тела давления» Wт.д и направлена вниз, если объем строится со смоченной стороны поверхности; если объем строится с несмоченной стороны поверхности, сила Рz направлена вверх.
В формулах (1) и (2) для Рх и Рz предполагается, что жидкость находится с одной стороны поверхности и с несмоченной ее стороны давление равно атмосферному.
Полная сила давления на поверхность представляет геометрическую сумму сил Рх и Рz:
 . (3)
. (3)
Линия действия силы Р проходит через точку пересечения линий действия сил Рх и Рz.
Угол j наклона равнодействующей к горизонту определяется из формулы
 . (4)
. (4)
Задача 31
Бензин (относительная плотность  =0,7) под избыточным давлением р = 30 кПа подводится к поплавковой камере карбюратора по трубке диаметром d = 4 мм. Шаровой поплавок массой 25 г и игла массой 12 г, перекрывающая доступ бензина, укреплены на рычаге a = 40 мм, b = 15 мм, который может поворачиваться вокруг неподвижной оси 0. Определить радиус r поплавка из условия, чтобы в момент открытия отверстия поплавок погружен наполовину (трением в шарнирах и весом рычага пренебречь).
=0,7) под избыточным давлением р = 30 кПа подводится к поплавковой камере карбюратора по трубке диаметром d = 4 мм. Шаровой поплавок массой 25 г и игла массой 12 г, перекрывающая доступ бензина, укреплены на рычаге a = 40 мм, b = 15 мм, который может поворачиваться вокруг неподвижной оси 0. Определить радиус r поплавка из условия, чтобы в момент открытия отверстия поплавок погружен наполовину (трением в шарнирах и весом рычага пренебречь).

Рисунок к задаче 31
Задача 32
Подводный железобетонный туннель круглого сечения с внутренним диаметром D = 3 м и толщиной стенки d = 250 мм удерживается от всплывания тросами Т, расположенными попарно через каждые 6 м длины туннеля. Определить натяжение тросов, полагая дополнительную нагрузку, приходящуюся на 1 м длины туннеля G = 10 кН, плотность бетона 2,5 т/м3.

Рисунок к задаче 32
Задача 33
Определить отрывающее усилие, воспринимаемое болтами полусферической крышки радиусом r = 0,5 м, если показание манометра Pо = 26487 н/м2. Глубина воды h=1,2 м.

Рисунок к задаче 33
Задача 34
Определить минимальную толщину стенок стального трубопровода диаметром d=60 см, находящегося под средним гидростатическим давлением Р =294,3•104 н/м2=30 атм. Допускаемое напряжение s = 13734×104 н/м2

Рисунок к задаче 34
Задача 35
Каков наименьший уровень Н воды в сосуде, при котором стальной шар (относительной плотностью s = 8) радиусом R = 100 мм, перекрывающий круглое отверстие диаметром d = 1,5 R в вертикальной стенке, будет находиться в равновесии?





Задача 36
Определить силу, прижимающую стальной (относительная плотность d = 8) шаровой всасывающий клапан радиусом R = 100 мм к седлу, имеющему диаметр d = 125 мм, если диаметр насосного цилиндра D = 350 мм, а усилие по штоку Р = 4000 Н. Седло клапана расположено ниже оси цилиндра на расстояние h1 = 0,5 м и выше свободной поверхности в резервуаре с атмосферным давлением на расстояние h2 = 6,5 м, причем труба под клапаном заполнена водой.

Рисунок к задаче 36
Задача 37
Поворотный пролет моста опирается на цилиндрический поплавок диаметром D = 3,4 м, плавающий в камере диаметром D1 = 3,6 м.
Определить: погружение а поплавка в воду, если масса пролета с поплавком m = 30 т; осадку h пролета при нагружении его внешней силой Р = 100 кН.

Рисунок к задаче 37
Задача 38
Смотровой люк в боковой стенке резервуара перекрывается полусферической крышкой диаметром d=0,6 м. Определить отрывающее Fx и сдвигающее Fz усилия, воспринимаемые болтами, если уровень бензина над центром отверстия H = 2 м. Показание манометра рм= 4,1 кПа.

Рисунок к задаче 38
Задача 39
Для автоматического поддержания уровня воды в резервуаре использован полусферический клапан диаметром d = 250 мм в дне. Определить массу груза т для поддержания уровня воды H = 3,2 м, если плечи рычага АВ = 0,6 м, ВС=1,4 м. Масса клапана mк=15 кг.

Рисунок к задаче 39
Задача 40
Погруженный в воду полый шаровой клапан диаметром D = 150 мм и массой m = 0,5 кг закрывает выходное отверстие внутренней трубы диаметром d = 100 мм. При какой разности уровней Н клапан начнет пропускать воду из внутренней трубы в резервуар?

Рисунок к задаче 40