Так как поток представляется совокупностью элементарных струек, то его энергия будет равна их сумме.
При плавно изменяющемся движении потенциальную энергию для каждой струйки можно считать величиной постоянной, а действительная кинетическая энергия потока будет несколько больше по сравнению с кинетической энергией, подсчитанной по средней скорости, поэтому для компенсации этого неравенства вводится скоростной коэффициент (коэффициент Кориолиса).
Таким образом, уравнение Бернулли для потока реальной жидкости имеет вид
,
где a - коэффициент Кориолиса, он зависит от режима движения жидкости.
Для ламинарного движения при Re < 2320 a = 2; для турбулентного при Re > 2320 a = 1,05…1,1 » 1,0.
Гидравлические потери
Причиной гидравлических потерь являются гидравлические сопротивления по длине потока и в местах изменения конфигурации потока. Соответственно потери напора делятся также на потери по длине (линейные) и местные.
Гидравлические потери существенным образом зависят от режима движения жидкости, который характеризуется числом Рейнольдса Re.
Для круглой трубы
,
где V – средняя скорость движения жидкости; d – диаметр трубы; r - плотность жидкости; m, n - соответственно динамический и кинематический коэффициенты вязкости.
При Re < 2320 режим ламинарный, при Re > 2320 режим турбулентный.
Линейные потери определяются по формуле Дарси-Вейсбаха
,
где l - коэффициент гидравлического трения или коэффициент Дарси, 
; l,d – соответственно длина и диаметр трубопровода; v – средняя скорость жидкости; 
– относительная шероховатость; D - абсолютная шероховатость.
Местные потери определяются по формуле
,
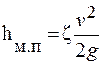где z - коэффициент местного сопротивления; зависит от вида местного сопротивления и режима движения жидкости. Для различных видов местных сопротивлений z находят индивидуально из таблиц, формул и графиков; v – средняя скорость в трубопроводе, в котором установлено местное сопротивление.
|
|
Задача 51
Вода перетекает из напорного бака А в резервуар Б через вентиль с коэффициентом сопротивления z =3 по трубе. Диаметры: d 
= 40 мм; d2=60 мм. Считая режим течения турбулентным и пренебрегая потерями на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Высоты: H1=l м, H2=2 м; избыточное давление в напорном баке р0= 0,15 МПа.
Рисунок к задаче 51
Задача 52
Для определения потерь давления на фильтре установлены манометры, как показано на рисунке. При пропускании через фильтр жидкости, расход которой Q = 1 л/с; давления: р1 = 0,1 МПа, р2 = 0,12 МПа. Определить, чему равна потеря давления в фильтре, если известно: d1 = 10 мм, d2 = 20 мм, rж = 900 кг/м3.
Указание. Потерей давления на участках от мест установки манометров до фильтра пренебречь. Принять a1a2 = 1.
Рисунок к задаче 52
Задача 53
Бензин сливается из цистерны по трубе диаметром d = 50 мм, на которой установлен кран с коэффициентом сопротивления zкр = 3. Определить расход бензина при Н1 = 1,5 м, Н2 = 1,3 м, если в верхней части цистерны имеет место вакуум hвак = 73,5 мм рт.ст. Потерями на трение в трубе пренебречь. Плотность бензина r = 750 кг/м3.
Рисунок к задаче 53
Задача 54
Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте Н = 2 м и постоянное давление Р2 = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d1 = 75 мм, показывает Р1 = 0,25 МПа. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку, d2 = 50 мм; коэффициент сопротивления этой трубы принят z = 0,5. Плотность жидкости r = 800 кг/м3.
|
|
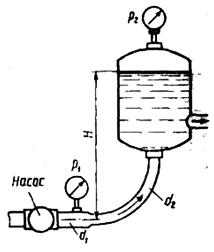
Рисунок к задаче 54
Задача 55
Заполнение бака бензином происходит через воронку диаметром d2 = 50 мм, высотой h = 400 м с коэффициентом сопротивления z = 0,25. В воронку бензин заливается из резервуара с постоянным уровнем по короткой трубе диаметром d1 = 30 мм с краном и угольником, коэффициенты сопротивления которых соответственно z = 8,5 и z = 0,8. Определить, какой наибольший напор Н можно иметь в резервуаре, чтобы воронка не переполнялась, и каков при этом расход бензина, поступающего в бак. Потери на трение по длине трубы не учитывать.
рисунок к задаче 55
Задача 56
Вода перетекает из левого бака в правый по трубопроводу, диаметры которого d1 = 100 мм и d2 = 60 мм. Определить, пренебрегая потерями трения по длине, расход в трубопроводе при располагаемом напоре Н = 3 м и коэффициенте сопротивления вентиля z = 5. Построить график напоров. При каком значении z расход уменьшится в два раза?
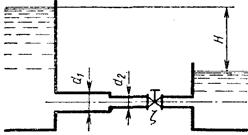
Рисунок к задаче 56
Задача 57
Вода вытекает в атмосферу по короткому горизонтальному трубопроводу, на котором установлен вентиль, под постоянным напором Н = 16 м. Диаметры участков трубопровода d1 = 50, d2 = 70 мм. Коэффициент сопротивления вентиля z = 4. Определить расход в трубе, учитывая только местные потери напора.
Построить линию полного напора и пьезометрическую линию.
|
|
Рисунок к задаче 57
Задача 58
Вода перетекает из напорного бака, где избыточное давление воздуха р = 0,3 МПа, в открытый резервуар по короткой трубе диаметром d = 50 мм, на которой установлен кран. Чему должен быть равен коэффициент сопротивления крана, чтобы расход воды составлял Q = 8,7 л/с? Высоты уровней Н1 = 1 м, Н2 = 3 м. Учесть потерю напора на входе в трубу (zвх = 0,5) и на выходе из трубы (внезапное расширение).
Рисунок к задаче 58
Задача 59
Определить напор, создаваемый насосом системы охлаждения автомобильного двигателя, при следующих данных: подача насоса Q = 3,9 л/с; коэффициенты сопротивления: блока цилиндров z1 = 3,5; термостата z2 = 2,5; радиатора z3 = 4,0; трубы (шланга) от радиатора до насоса z4 = 2,0. Все коэффициенты отнесены к скорости в трубе диаметром d = 40 мм. Чему равно абсолютное давление перед входом в насос, если в верхней части радиатора возник вакуум rвак = 1 кПа; высота Н = 0,4 м; атмосферное давление соответствует hа = 750 мм рт.ст., rж = 1000 кг/м3.
Рисунок к задаче 59
Задача 60
От бака, в котором с помощью насоса поддерживается постоянное давление жидкости, отходит трубопровод диаметром d = 50 мм. Между баком и краном К на трубопроводе установлен манометр. При закрытом положении крана р0 = 0,5 МПа. Найти связь между расходом жидкости в трубопроводе Q и показанием манометра р при разных открытиях крана, приняв коэффициент сопротивления входного участка трубопровода (от бака до манометра) z = 0,5. Плотность жидкости r = 800 кг/м3.
Подсчитать расход жидкости при полном открытии крана, когда показание манометра р = 0,485 МПа.
Рисунок к задаче 60