Идея приближенного метода была изложена И.Г. Бубновым в отзыве на работу С.П. Тимошенко по устойчивости упругих систем в 1913 году и затем, впоследствии был развит Б.Г. Галеркиным. Этот метод решения задач в перемещениях основан на использовании первой вариации энергии, которая равна нулю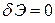 
. Вариация энергии приводит к уравнению равновесия и статическим граничным условиям. На аппроксимирующие функции прогиба накладывается требование удовлетворения геометрическим граничным условиям. Если выбранные функции удовлетворяют и статическим граничным условиям, то остается удовлетворить полученному уравнению равновесия. Рассмотрим это подробнее. Запишем полную энергию пластины в форме (4.3).
.
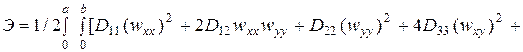
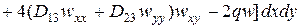Проварьируем выражение энергии для ортотропной пластины по функции прогиба (В 13 = В 23 = 0) и проинтегрируем по частям производные от вариации функции прогиба. В результате получим под интегралом уравнение равновесия изгиба пластин и статические граничные условия на ее краях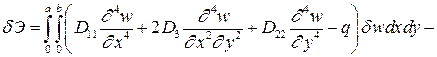 
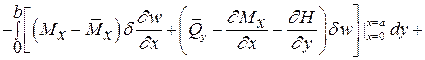
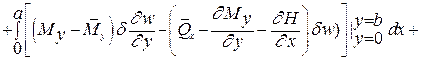
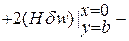
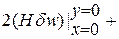
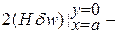
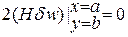
Последнюю строчку обычно не учитывают.
Если функция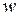 
удовлетворяет не только геометрическим граничным условиям, но и статическим условиям на границе пластины, то тогда остается удовлетворить только уравнениям равновесия. Если для шарнирного края выбрана функция прогиба, только удовлетворяющая условию 
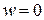, то эта функция не обеспечивает равенство нулю моментов и тогда выражение для соответствующего момента на границе должно остаться в общем решении.
Рассмотрим более подробно метод на примере одномерной задачи. Пусть решение некоторой задачи связано с минимумом функционала вида
.
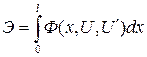Тогда вариация функционала равна нулю и принимает вид
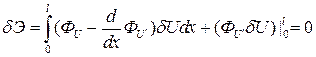
или
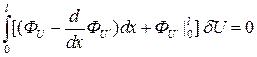, но т.к. 
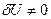, то выражение в квадратных скобках равно нулю.
|
|
Предположим, что статические граничные условия удовлетворены, тогда предыдущее выражение примет вид
,
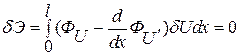а подынтегральный функционал преобразуется к дифференциальному выражению
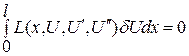, (4.6)
где L - дифференциальный оператор. Приближенное решение можно искать в виде ряда
,
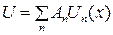где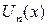 
- заданные функции, 
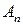- неизвестные коэффициенты.
Тогда вариация функции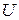 
запишется в виде
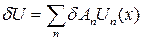, (4.7)
где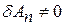 
, а выражение (4.6) примет вид с учетом (4.7)
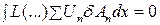. (4.8)
В (4.8) после подстановки ряда 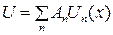с учетом того, что выражение равно нулю, то в нуль должно обращаться каждое слагаемое при независимом коэффициенте 
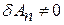, то есть
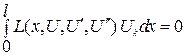, (4.9)
где индекс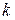 
есть номер слагаемого из ряда n.
То есть выбранный ряд мы должны подставить в подынтегральное выражение, умножить на заданную функцию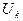 
и проинтегрировать. Полученную систему алгебраических уравнений решаем относительно искомых коэффициентов 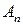. Этот метод решения можно рассматривать как приближенный метод интегрирования дифференциальных уравнений. С другой стороны, с точки зрения математики, условие (4.9) есть процедура ортогонализации выбранной функции между собой, т. e. мы требуем, чтобы ошибка выбранной функции стремилась к нулю. Для упрощения решения желательно, чтобы выбранные перемещения выбирались по ортогональным функциям.
Рассмотрим пример. Найдем прогиб шарнирно опертой пластины с размерами сторон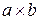 
, с координатами 
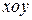, началом координат в угловой точке пластины и нагруженной равномерной нагрузкой 
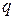(рис.4.2). Этому условию закрепления отвечает тригонометрический ряд
.
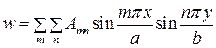На границах пластины сама функция и ее вторая производная, то есть прогиб и моменты, равны нулю. В соответствии с методом Бубнова-Галеркина для изотропной пластины каждое разрешающее алгебраическое уравнение имеет вид
|
|
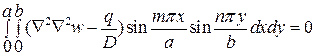. (4.10)
Для симметричного прогиба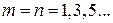 
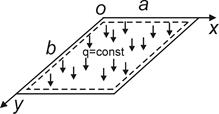
Рис. 4.2. Геометрия, координаты и нагрузка на пластину
Подставляя тригонометрический ряд в (4.10), получаем выражение
.
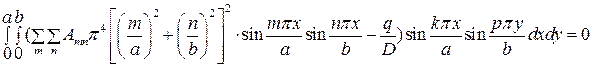Откуда после интегрирования с учетом ортогональности заданных функций находим коэффициенты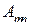 
.
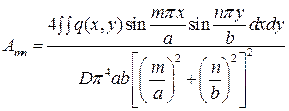В случае, когда поверхностная нагрузка 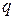постоянна, то коэффициент равен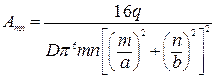 
и функция прогиба имеет вид
(
).
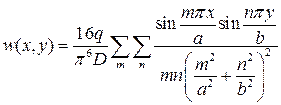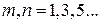Как видно из приведенного вычисления для квадратной пластины этот ряд быстро сходится
.
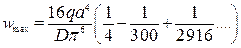