Расчет подкрепленных пластин, у которых подкрепления расположены достаточно часто решаются теми же способами, которые были рассмотрены раньше. Жесткость подкрепления с учетом их геометрии размазывается по ширине пластины и приводится к тем же известным цилиндрическим жестокостям, после чего и производится расчет пластины на изгиб. Высота подкрепления обычно соизмерима с шагом между стрингерами. Подкрепления бывают следующих видов: П - образный профиль, есть самый общий (рис.4.6); из него остальные получаются как частный случай: T – образный профиль (стенка в середине полки), Z – образный профиль и подкрепления в виде ребра (рис.4.7)
Рис. 4.6. Общий вид стрингерного подкрепления
Для определения средних цилиндрических жесткостей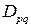 
с учетом подкрепляющих элементов рассмотрим в панели выделенный элемент, шириной 
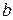(расстояние между стрингерами), который содержит сам профиль с присоединенной к нему обшивкой. Ширина расчетной обшивки определяется расстоянием между стрингерами , 
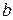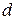- ширина полки -2, 
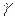- технологический угол, 
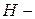высота профиля (стенки 1), 
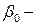ширина основания П – образного профиля, 
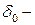расстояние от основания профиля до центра тяжести. На рис. 4.7 приведены возможные типы подкрепленных панелей.
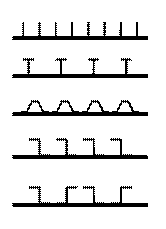
Рис. 4.7. Типы подкрепленных панелей
Вычислим изгибную жесткость рассматриваемого профиля с учетом обшивки (4.6). Для каждого элемента жесткости di равны:
,
, 
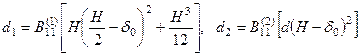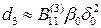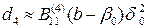, (4.21)
где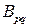 
- жесткость элементов вдоль продольной оси с учетом их толщины. Из конструктивно-технологических соображений можно принять 
, 
, 
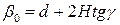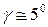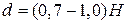. Тогда положение центра тяжести 
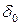относительно оси x вычисляется по формуле
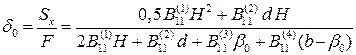. (4.22)
Здесь Sx - статический момент с учетом жесткости участков профиля, F - жесткость сечения. В этих характеристиках учитываются площади и упругие характеристики участков профиля, т. к. характеристики будут разными для разных участков. Тогда цилиндрическая жесткость элемента в направлении продольной оси будет равна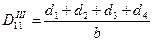 
. Другие цилиндрические жесткости для П – образного профиля вычисляются по формуле
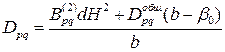(здесь Dpq есть 
, 
, 
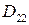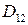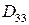для обшивки).
Для остальных профилей цилиндрические жесткости 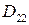, , 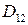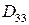равны цилиндрическим жесткостям обшивки.
Для профиля первого типа (оребренная панель) в записанных соотношениях (4.21) и (4.22) надо принять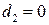 
(ширина полки 
), 
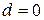(здесь 
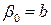), вертикальные стенки объединяются в одну и тогда 
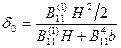и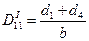 
.
Для профиля второго типа (Т – образного) в соотношениях (4.21) и (4.22) надо принять (здесь 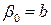), тогда с учетом объединения вертикальных стенок запишем
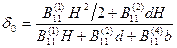и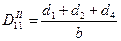 
.
разделены пополам на расстояние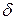 
. В соответствии с обозначениями рисунка 4.8 общую формулу цилиндрической жесткости ортотропной панели можно представить в виде
.
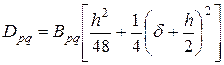Обозначая через D выражение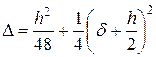 
, представим цилиндрическую жесткость в форме 
.
 |
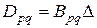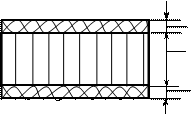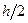
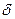
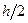
Рис. 4.8. Геометрия трехслойной пластины
Изгиб подкрепленных и трехслойных пластин ничем не отличается от расчета гладких пластин.
Рассмотрим гофрированную пластину типа стенки лонжерона (рис.4.9). Пусть каждый гофр описывается формулой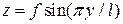 
, где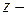 
координата по нормали к панели, 
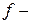максимальная высота гофра, 
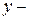поперечная координата панели, 
проекция гофра на координату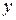 
, 
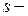длина полуволны гофра по его поверхности. Гофры увеличивают изгибную продольную жесткость пластины 
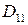, а также сдвиговую жесткость за счет увеличения поперечной длины панели 
(
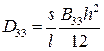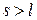). Остальные цилиндрические жесткости вычисляются по формулам
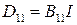, где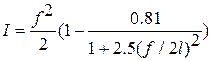 
, 
, 
, 
.
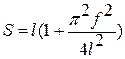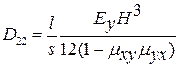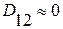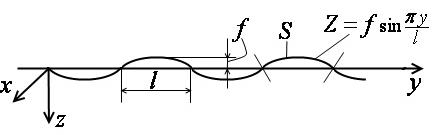
Рис. 4.9. Геометрия гофрированной пластины