Рассмотрим применение метод Власова – Канторовича к расчету треугольных и скошенных пластин. Перейдем от ортогональной системы координат (x, y) к косоугольной системе (r, 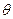 ) по формулам [5]:
) по формулам [5]:
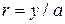 ,
, 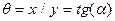 ,
, 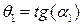 ,
, 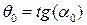 . (4.14)
. (4.14)
Рассмотрим пластину из квазиизотропного материала (рис.4.5). Примем, что цилиндрические жесткости 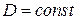 и в общем случае
и в общем случае 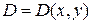 . Для решения задачи изгиба пластин применим принцип Лагранжа. Считаем справедливыми гипотезы Кирхгоффа, а полная энергия имеет вид:
. Для решения задачи изгиба пластин применим принцип Лагранжа. Считаем справедливыми гипотезы Кирхгоффа, а полная энергия имеет вид:
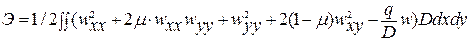
Переход к координатам (r, 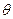 ) осуществляется с помощью следующих равенств:
) осуществляется с помощью следующих равенств:
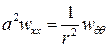 ;
; 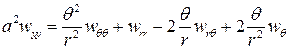 ;
;
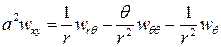 . (4.15)
. (4.15)
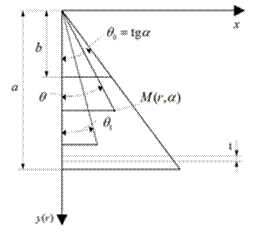
Рис. 4.5. Треугольная пластина
Заменяя переменные в двойном интеграле в выражении энергии с помощью (4.15), получим
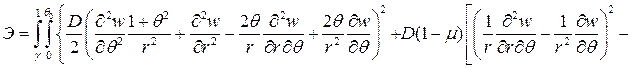
 , (4.16)
, (4.16)
где 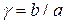 .
.
Согласно используемому методу функцию прогиба представим в виде конечного ряда:
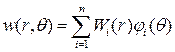 , (4.17)
, (4.17)
где через 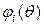 обозначены выбираемые функции. Подставляя разложение (4.17) в (4.16), получим
обозначены выбираемые функции. Подставляя разложение (4.17) в (4.16), получим
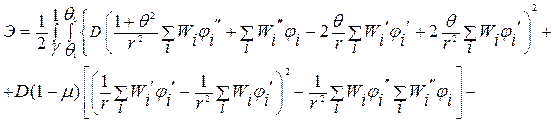
.
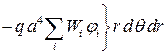 (4.18)
(4.18)
После интегрирования в (4.18) функции 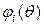 по
по 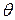 выражение (4.18) представляет собой функционал вида
выражение (4.18) представляет собой функционал вида
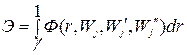 .
.
Согласно принципу Лагранжа функция 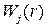 , реализующая минимум функционал, должна удовлетворять уравнению Эйлера-Лагранжа
, реализующая минимум функционал, должна удовлетворять уравнению Эйлера-Лагранжа
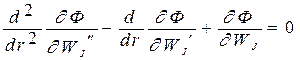
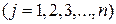 .
.
В развернутом виде это уравнение примет вид
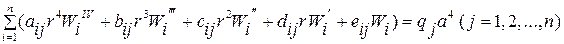 , (4.19) где
, (4.19) где 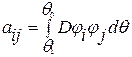 ,
, 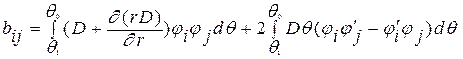 ,
,
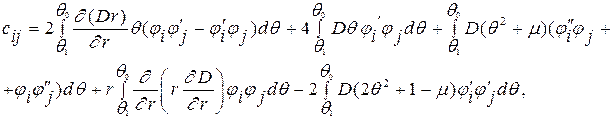
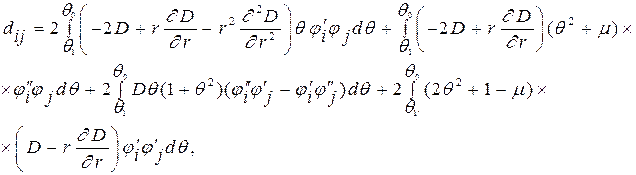
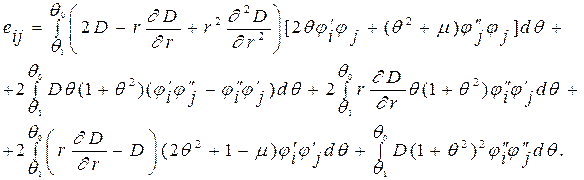
Если края пластины 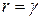 и
и 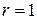 свободны от закрепления, то естественные граничные условия имеют вид:
свободны от закрепления, то естественные граничные условия имеют вид:
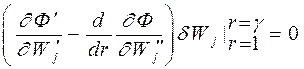 ;
; 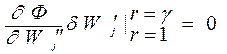 .
.
Рассмотрим решение в случае одночленной аппроксимации. Примем, что жесткость в пластине 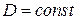 . Для треугольной пластины на границе
. Для треугольной пластины на границе 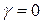 , где сходятся обе стороны в вершине, имеем особенность, поэтому при определении констант решение задачи из условия регулярности решения в этой точке константы решения в этой точке необходимо принять нулю. Для данной задачи имеется аналог выбираемой функции, который был рассмотрен в предыдущей задаче для прямоугольной пластины. Для выбора функции рассмотрим балку единичной ширины. В треугольной пластинке
, где сходятся обе стороны в вершине, имеем особенность, поэтому при определении констант решение задачи из условия регулярности решения в этой точке константы решения в этой точке необходимо принять нулю. Для данной задачи имеется аналог выбираемой функции, который был рассмотрен в предыдущей задаче для прямоугольной пластины. Для выбора функции рассмотрим балку единичной ширины. В треугольной пластинке 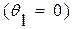 принимаем для косоугольной системы координат
принимаем для косоугольной системы координат 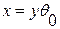 . Прогиб в этом случае примет вид
. Прогиб в этом случае примет вид 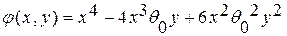 .
.
|
|
Заменяя здесь 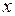 и
и 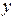 через
через 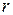 и
и 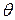 с помощью формул (4.14) и отбрасывая множитель
с помощью формул (4.14) и отбрасывая множитель  , который может быть отнесен к функции
, который может быть отнесен к функции 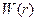 , окончательно получим
, окончательно получим
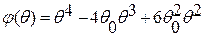 .
.
Для косоугольной пластинки:
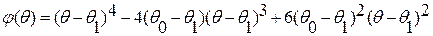
При одночленной аппроксимации разрешающее уравнение (4.19) для треугольной пластинки примет вид:
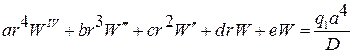 , (4.20)
, (4.20)
где 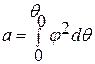 ,
, 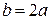 ,
,
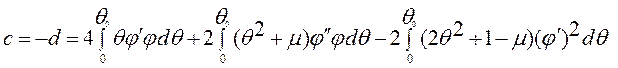 ,
,
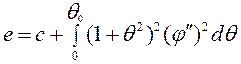 ,
, 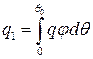 .
.
Граничные условия при 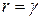 и
и 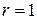 запишутся в виде
запишутся в виде
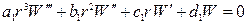 ;
;
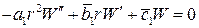 ,
,
где 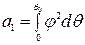 ,
, 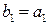 ,
, 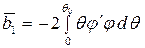 ,
,
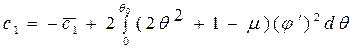 ,
,
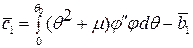 ,
, 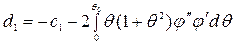 .
.
Уравнение (4.20) есть уравнение типа Эйлера. Решение этого уравнения будем искать в виде 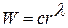 .
.
Подставляя в уравнение (4.20) получим для однородного уравнения характеристическое уравнение:
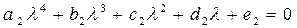 ,
,
где 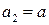 ,
, 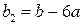 ,
, 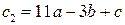 ;
; 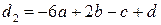 ;
; 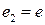 .
.
К общему решению однородного уравнения необходимо добавить частный интеграл, вид которого определяет поверхностная нагрузка.
В качестве примера рассмотрим треугольную пластину с углом стреловидности по передней кромке  . Выбирая решение в виде
. Выбирая решение в виде
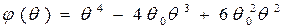 ,
,
и вычисляя коэффициенты уравнения, запишем его в виде
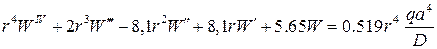 .
.
Характеристическое уравнение примет вид
 .
.
Решение этого уравнения дает два отрицательных действительных корня и два комплексных корня, которые равны
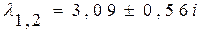 .
.
В общем виде решение задачи запишется в форме
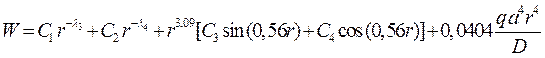 .
.
Действительные корни в точке 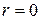 дают бесконечность, то есть нарушают регулярность решения задачи и поэтому коэффициенты
дают бесконечность, то есть нарушают регулярность решения задачи и поэтому коэффициенты 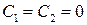 . Решение уравнений естественных граничных условий для края
. Решение уравнений естественных граничных условий для края 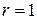 дает значение двух других констант
дает значение двух других констант
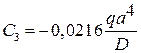 ,
, 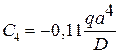 .
.
По расчету максимальный прогиб пластины в угловой точке равен
|
|
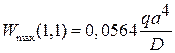 .
.
Экспериментальное значение прогиба дало результат
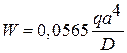 .
.
Сравнение результатов показывает, что аналитическое решение дает хорошее совпадение с экспериментом и может использоваться как в расчетах, так и в задачах проектирования.