Приложение 3. Пример оформления ПЗ

 

Введение

 

Целью работы является развитие и закрепление практических навыков разработки программ с использованием технологии структурного программирования на примере решения задачи об обработке результатов измерений по методу наименьших квадратов. Ее значение заключается в том, что разработчик на основе своих знаний разрабатывает и реализует программный комплекс, демонстрируя знание и владение системой программирования Turbo Pascal.

1 Описание решения

 

1.1 Постановка задачи

 

Даны 10 пар чисел (x_i,y_i) вещественного типа, где i от 1 до 10. Произвести обработку данных по методу наименьших квадратов, то есть найти параметры в формулах

так, чтобы , где , для каждой из этих формул была минимальной.

 

1.2 Спецификация программы

1.2.1 Название задачи

Даны 10 пар чисел (x_i,y_i) вещественного типа, где i от 1 до 10. Произвести обработку данных по методу наименьших квадратов, то есть найти параметры в формулах

так, чтобы , где , для каждой из этих формул была минимальной.

Название программного комплекса: ” Обработка результатов измерений по методу наименьших квадратов ”.

Система программирования: Turbo Pascal 7.0.

Требования к аппаратному обеспечению:

Ø Процессор: Pentium 133 МГц или выше;

Ø ОЗУ: 16 Мб;

Ø Видеокарта: 2 Мб;

Ø операционная система: Windows 98/Me/2000/XP;

Ø клавиатура

1.2.2 Описание

Для оптимальных значений параметров a₀,a₁ линейной регрессии справедлива система уравнений

где , (1)

вывод которой дается в [1].

Оптимальным значениям параметров a₀, a₁, a₂ параболической регрессии соответствует система

, (2)

вывод которой представлен там же. Решив эту систему (например, методом Гаусса), получим:

, (3)

где , , , , , .

 

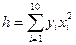Для нахождения параметров A, k в экспоненциальной регрессии представим ее в виде где a₀=ln A, a₁=k, 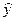= ln y, то есть составим пары () и найдем параметры a₀, a₁ из системы (1) для этих пар. Тогда , .

Определение параметров A и v в степенной регрессии происходит аналогичным образом с той лишь разницей, что необходимо составить пары (), где 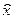= ln x,

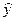= ln y. Тогда , .

Необходимо учитывать, что значения экспоненциальной функции всегда одного знака и не равны нулю. К тому же значение этой зависимости при x=0 равно значению параметра A, который заранее не известен. Исходя из этого, для избежания больших погрешностей стоит исключить исследование экспоненциальной регрессии в следующих случаях:

· хотя бы одно из исходных значений равно 0;

· значения y_i не одного знака.

Используемые методы вычисления неизвестных параметров в экспоненциальной и степенной регрессиях предусматривают использование только положительных исходных значений.

В экспоненциальной регрессии для расширения области значений исходных данных будем действовать по следующей схеме

 

.

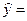
Значения y=0 заранее исключаются. После вычисления искомых параметров к значению A дописывается минус, если y<0. Мы можем воспользоваться этим приемом вследствие того, что противоположные по знаку экспоненциальные функции симметричны относительно оси Ox (рис. 1(а), 1(б)).

рис. 1(а)

рис. 1(б)

В степенной регрессии для расширения области значений исходных данных будем также присваивать 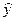значение , а значениям 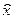- значение . Это можно сделать вследствие симметричности графика степенной функции относительно оси Oy или начала координат (рис. 2(а), 2(б), 2(в), 2(г)).

рис. 2(а)

рис. 2(в)

рис. 2(б)

рис. 2(г)

 

Метод вычисления параметров v и A показан выше. Значение v оставляем без изменений. Знак же параметра A необходимо установить. Для этого проверяем, одного ли знака все значения x. Если нет, то находим два противоположных по знаку значения x (пары предварительно упорядочены по возрастанию x). Пусть это будут пары и . Перед параметром A допишем знак ‘-‘, если y₄<0 и y₅<0 или y₄>0 и y₅<0. Иначе, оставим параметр A без изменения.

Если же все значения x одного знака без нулей, то исследуем получившуюся функцию на четность. Допишем знак ‘-‘ перед значением параметра A, если:

o все x>0, все y<0;

o все x<0, y₅>0, функция нечетная;

o все x<0, y₅<0, функция четная;

В других случаях знак перед значением параметра A оставим без изменений.

1.2.3 Управление режимами работы

Пользователь программы может:

Ø вводить исходные данные вручную;

Ø вводить исходные данные из файла;

Ø пользоваться справкой;

Ø выходить из программы.

Осуществление этих действий производится посредством выбора пунктов главного меню программы или нажатия специальных клавиш:

<F1> - для вызова справки;

<F2> - для ввода исходных данных вручную;

<F3> - для ввода исходных данных из файла;

<ESC> - для выхода из программы.

После вызова справки на экран выводится меню справки, вернуться в главное меню из которого можно нажав клавишу <ESC>. Просмотр разделов справки производится выбором пунктов меню справки с помощью клавиш управления курсором и <Enter>. Возвращение в меню справки происходит посредством нажатия клавиши <Enter>.

После выбора пункта Ввод исходных данных вручную на экран выводится форма ввода. Вернуться в главное меню можно, набрав символ вместо числа и отрицательно ответить в появившемся окне. После ввода исходных данных на экран выводятся введенные данные. Вернуться в главное меню с этого этапа можно, нажав <ESC>. Для продолжения необходимо нажать <ESC>. Если среди введенных данных есть нули или не все значения y одного знака, то выводится сообщение об исключении исследования экспоненциальной регрессии. Далее на экране появляется таблица с отклонениями по каждой из получившихся функций, а также формула наиболее приемлемой зависимости и запрос о выводе результата в файл. Если пользователь отвечает положительно, то появляется поле ввода, куда необходимо ввести желаемое имя файла. После этого (или вместо) пользователь возвращается в главное меню.

При выборе пункта Ввод исходных данных из файла на экран выводится окно с полем, куда необходимо ввести путь к файлу с данными или просто имя файла (с расширением.txt), если файл находится в папке программы. Для возвращения в главное меню необходимо в это поле ввести EXIT или exit. Дальнейшие действия аналогичны действиям при вводе данных вручную.

При выборе пункта Выход появляется запрос о подтверждении выхода.

1.2.4 Входные данные

Значения x и y могут быть в диапазоне от –999999.999 до 999999.999, в том числе и равными нулю, однако не сколь угодно близкими к нулю. В файле с исходными данными значения x должны располагаться через пробел в первой строке, значения y – во второй. Формат чисел: 999.999 (НЕ 999,999!); между знаком ‘-‘ и числом нет пробела.

1.2.5Выходные данные

Выходными данными являются значения искомых параметров. Они выводятся на экран, вставленные в соответствующие им формулы. В файл выводятся наиболее приемлемая формула и исходные данные.

1.2.6 Ошибки

При работе с программой пользователь может допустить следующие ошибки:

1. При вводе исходных данных вручную: ввод нечислового значения. При этом появляется сообщение об ошибке с запросом о повторении ввода. Повторный ввод начинается с неверно введенного элемента. Для защиты от этой ошибки следует предварительно присваивать введенное значение переменной строкового типа, а затем с помощью процедуры Val преобразовать эту переменную в число и присвоить его соответствующему x или y. После этого производится обработка кода ошибки преобразования. Код ошибки, не равный 0, свидетельствует об ошибке преобразования, то есть о нечисловом формате данных.

2. При вводе исходных данных из файла: неправильный путь к файлу, неверное имя файла или неготовность устройства. При этом появляется сообщение об ошибке с запросом о повторном вводе. При положительном ответе вновь выводится окно с полем ввода, при отрицательном – на экран выводится главное меню. Для защиты от этой ошибки перед связыванием внешнего файла исходных данных с некоторой файловой переменной (процедура Assign) дать директиву компилятору {$I-}, чтобы отключить автоматическую проверку ошибок ввода/вывода. После связки помещается директива {$I+}, вновь включающая проверку. Затем проверяется значение, возвращенное функцией IOResult. Если это значение не равно 0, то произошла ошибка ввода/вывода.

3. При вводе исходных данных из файла: недостаточное количество чисел в файле в одной из строк или в обеих сразу; в строках есть символы, отличные от цифр, точки и знака ‘-‘; неверно записано число (например, -99..5). При возникновении одной из этих ошибок на экран выводится сообщение об ошибке, исследование прекращается и на экран выводится главное меню. Для обхода этой ошибки следует считывать символы до пробела в строковую переменную, а затем преобразовывать в значение x или y с помощью процедуры Val, как было описано выше.

1.2.7 Пример работы программного комплекса

Пользователь выбирает пункт Ввод исходных данных из файла. На экране появляется окно с полем для ввода пути к файлу. Путь к файлу с данными:”C:\Research\data.txt”. Содержание файла:

-5 -4 -3 -2 -1 0 1 2 3 4

0.15 0.25 0.36 0.45 0.56 0.68 0.82 0,96 1.06

Пользователь вводит “C:Reserch\data.txt” и нажимает <Enter>. На экран выводится сообщение об ошибке ввода/вывода с запросом о повторном вводе. Пользователь набирает в этом окне <y> и нажимает <Enter>. Снова появляется окно с полем ввода. Пользователь набирает в нем “C:\Research\data.txt” и нажимает <Enter>. Появляется сообщение об ошибке считывания данных из файла по причине их нехватки или неверного ввода. Исследование прекращается, на экран выводится главное меню.

 

1.3 Проектирование программы

Общая структура программного комплекса:

Диаграмма потоков данных:

 

 

Блок-схемы алгоритмов вычислений искомых параметров для линейной регрессии:

 

 

 

1.4 Кодирование

Файлы программного комплекса:

1. MAIN.EXE содержит основную программу. Процедура MenuToScr организовывает вывод на экран главного меню программы.

2. Calcul.tpu содержитматематические и логические функции и процедуры, включая процедуры по вычислению искомых параметров задачи.

Функция Add(arr: array of real): real находит сумму элементов массива Arr.

Функция Max(arr: array of real): real находит максимальный элемент массива Arr.

Функция RelZ(arr: array of real): boolean – истина, если элементы Arr одного знака (или ноль).

Функция MoreZ(arr: array of real): boolean – истина, если массив Arr состоит из положительных чисел (без нуля).

Функция ZeroIs(arr: array of real): boolean – истина, если среди элементов массива Arr есть нули.

Функция Change(ax, ay: array of real): menu равна 1, если выполнены условия исследования всех четырех функций, и равна 2, если нет.

Функция TheBest(dlin, dpar, dexp, dsig: real): integer равна

o 1, если наиболее подходящей является линейная зависимость;

o 2, если параболическая;

o 3, если экспоненциальная;

o 4, если степенная.

Обработка ведется по наибольшим отклонениям каждой функции от исходных данных dlin, dpar, dexp, dsig.

Процедура LinReg(ax, ay:array of real; var coef0, coef1, dmax: real; var dmas: array of real) осуществляет вычисление параметров coef0 и coef1 для линейной регрессии по данным массивов ax и ay. А также составляет массив отклонений dmas получившейся зависимости от исходных данных и находит максимальное из этих отклонений dmax.

Процедура Procedure ParReg(ax, ay: array of real; var coef0, coef1, coef2, dmax: real; var dmas: array of real) осуществляет вычисление параметров coef0, coef1 и coef2 для параболической регрессии по данным массивов ax и ay. А также составляет массив отклонений dmas получившейся зависимости от исходных данных и находит максимальное из этих отклонений dmax.

Процедура ExpReg(ax, ay: array of real; vars coef, pow, dmax: real; var dmas: array of real) осуществляет вычисление параметров coef и pow для экспоненциальной регрессии по данным массивов ax и ay. А также составляет массив отклонений dmas получившейся зависимости от исходных данных и находит максимальное из этих отклонений dmax.

Процедура SigReg(var ax, ay: array of real; var coef, pow, dmax: real; var dmas: array of real) осуществляет вычисление параметров coef и pow для степенной регрессии по данным массивов ax и ay. А также составляет массив отклонений dmas получившейся зависимости от исходных данных и находит максимальное из этих отклонений dmax.

3. IOPut.tpu содержит процедуры ввода и вывода данных, а также оформления экрана.

Процедура InpHnd организовывает ввод данных вручную.

Процедура InpFile организовывает ввод данных из файла.

Процедура Analyze(masx, masy: array of real) производит вывод промежуточной информации и результатов на экран.

Процедура Border обрамляет экран рамкой из специального символа.

Процедура Ramka(x0, y0, x1, y1, bc: integer) обрамляет окно сообщения с координатами левого верхнего угла x0, y0, координатами правого нижнего угла x1, y1 и цветом главного окна bc.

Процедура Table(n: integer) рисует таблицу с n столбцами.

4. Preview.tpu содержит процедуру Zastavka, организовывающую вывод заставки на экран.

5. HelpC.tpu содержит процедуру Contest, организовывающую вывод на экран меню справки и справочных статей.

1.5 Тестирование программы

Наборы данных для тестирования приведены в Таблице №1.

Таблица №1

№ набора	i
	xi	-2.0	-1.5	-1.0	-0.5	0.0	0.5	1.0	1.5	2.0	2.5
yi	11.3	13.2	14.1	13.0	10.9	7.9	7.9	3.8	-1.3	-7.4

Продолжение таблицы №1

№ набора	i
	xi	-3.0	-2.5	-2.0	-1.5	-1.0	-0.5	0.0	0.5	1.5	2.5
yi	-3.2	-1.8	-0.4	0.9	2.3	3.6	5.0	6.4	9.1	11.3
	xi	-2.5	-2.0	-1.5	-1.0	-0.5	0.0	0.5	1.0	1.5	2.0
yi	11.0	8.5	6.7	5.2	4.0	3.1	2.4	1.9	1.5	1.2
	xi	-5.0	-4.0	-3.0	-2.0	-1.0	0.0	1.0	2.0	3.0	4.0
yi	-10.0	-8.0	-6.0	-4.0	-2.0	0.0	2.0	4.0	6.0	8.0
	xi	-5.0	-4.0	-3.0	-2.0	-1.0	0.0	1.0	2.0	3.0	4.0
yi	125.0	64.0	27.0	8.0	1.0	0.0	-1.0	-8.0	-27.0	-64.0
	xi	-10.0	-9.0	-8.0	-7.0	-6.0	-5.0	-4.0	-3.0	-2.0	-1.0
yi	-0.013	-0.022	-0.037	-0.06	-0.1	-0.16	-0.27	-0.45	-0.74	-1.21
	xi	-5.0	-4.0	-3.0	-2.0	-1.0	0.0	1.0	2.0	3.0	4.0
yi	39.0	24.0	13.0	6.0	3.0	4.0	9.0	18.0	31.0	48.0

 

Результаты:

1. , макс. отклонение 5.5;

, макс. отклонение 1.7;

, макс. отклонение 12.61;

2. , макс. отклонение 0.3;

, макс. отклонение 0.2;

, макс. отклонение 8.9;

3. , макс. отклонение 1.8;

, макс. отклонение 0.3;

, макс. отклонение 6.4;

4. , макс. отклонение 0;

, макс. отклонение 0;

, макс. отклонение 0.6;

5. , макс. отклонение 43.8;

, макс. отклонение 25;

, макс. отклонение 0;

6. , макс. отклонение 0.4;

, макс. отклонение 0.1;

, макс. отклонение 0;

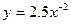, макс. отклонение 1.3;

7. , макс. отклонение 24;

, макс. отклонение 0;

, макс. отклонение 17.6.

 

Трассировочная таблица для набора № 4 (процедура LinReg):

 

Таблица №2

Строка

Ход выполнения

midx

k

ar11

ar12

ar13

ar14

ar15

ar16

ar17

ar18

ar19

ar110

ar21

ar22

ar23

ar24

ar25

ar26

ar27

ar28

ar29

ar210

coef0

coef1

Вход в LinReg

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

-0,5

Начало цикла

20,25

12,25

6,25

2,25

0,25

0,25

 

Продолжение таблицы №2

Строка

Ход выполнения

midx

k

ar11

ar12

ar13

ar14

ar15

ar16

ar17

ar18

ar19

ar110

ar21

ar22

ar23

ar24

ar25

ar26

ar27

ar28

ar29

ar210

coef0

coef1

2,25

6,25

12,25

20,25

Выход из цикла

Выход из LinReg

2. Анализ результатов

2.1 Оценка стиля программирования

Оценка стиля программирования приведена в Таблице № 3.

Таблица № 3

Критерий оценки	Значение	Вес
1. Длина модуля		15%
2. Длина идентификатора		14%
3. Процент строк комментариев		10%
4. Процент отступов	16,2	10%
5. Процент пустых строк		0%
6. Число символов в строке		9%
7. Добавленные пробелы		4%
8. Процент определения констант		0%
9. Служебные слова		5%
10. Включаемые файлы		0%
	Итого:	67%

2.2 Анализ временной сложности программы

Построение аналитического профиля приведено в Таблице № 4.

Таблица № 4

Номер строки	Профиль	Аналитический профиль	Текст программы
			BEGIN
			midx:=Add(ax)/10;
			for k:=0 to 9 do
			begin
			ar1[k]:=ay[k]*(ax[k]-midx);
			ar2[k]:=sqr(ax[k]-midx);
			end;
			coef1:=Add(ar1)/Add(ar2);
			coef0:=Add(ay)/10-coef1*midx;
			for k:=0 to 9 do
			dmas[k]:=abs(ay[k])-abs(coef0+coef1*ax[k]);
			dmax:=Max(dmas);
			END.

Для построения оценки сформируем таблицу:

Таблица № 5

<

Номер строки	Аналитический профиль	Условное время однократного выполнения	Общее время выполнения строки

⇐ Предыдущая12

Поделиться: