Для оценки физических параметров газов часто используют уравнения состояния идеального газа. К ним относятся:
1) Закон Бойля-Мариотта
2) Закон Гей-Люсака
3) Закон Шарля
Общая зависимость между объемом, давлением и температурой для газа имеет вид:
(10)
где Ро, Vo (Vст), То (Тст) - параметры газа при нормальных или стандартных условиях.
Обобщенное уравнение состояния идеального газа Клайперона-Менделеева, выведенное на основе (1) с учетом закона Авогадро, имеет вид:
(11)
где n - число молей; 
- универсальная (молярная) газовая постоянная.
Численное значение постоянной можно получить, введя в уравнение (11) молярный объем 
при Р = Ро = 0,101325 МПа и То = 273,15 °К:
,
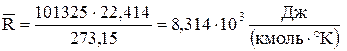то есть универсальная газовая постоянная численно равна работе расширения 1 кмоль идеального газа при повышении температуры на 1 °К и не зависит от природы газа.
Так как число молей газа равно n = G / Мг, то обобщенное уравнение состояние для произвольной массы газа будет иметь вид:
, (12)
где 
- удельная газовая постоянная, 
.
Для расчета состояния реальных газов пользуются уравнением (12), в которое вводится коэффициент сверхсжимаемости, учитывающий отклонение реальных газов от идеальных:
, (13)
Величина z является двумерной функцией и зависит от приведенных значений давления и температуры, т.е. z = f (Pпр,Тпр). Для реального природного или попутного газа приведенные параметры давления и температуры равны:
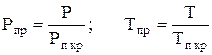, (14)
где Р, Т - действительные давления и температура;
- псевдокритические (среднекритические) параметры газа, вычисляемые по правилу аддитивности при известных молярных концентрациях компонентов в смеси и их критических параметрах Ркрi и Tкрi.
Приведенные параметры смеси углеводородных и небольшого (до 5%) количества неуглеводородных газов (без азота) можно определить по аппроксимационным формулам Ляпкова П. Д.:
|
|
, (15)
где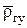 
- относительная по воздуху плотность смеси газов (кроме азота), которую можно определить по относительной (по воздуху) плотности всего газа при стандартных условиях:
, (16)
где 
- относительная плотность азота по воздуху, равная 0,97; 
- относительная плотность всего газа; yа - молярная доля азота при стандартных условиях.
Коэффициент сверхсжимаемости газовой смеси, состоящей из углеводородных компонентов и азота, определяют по следующей формуле:
, (17)
где 
и 
- коэффициенты сверхсжимаемости углеводородной части газа (графики Брауна и Катца) и азота; 
- объемная (молярная) доля углеводородной части газа.
При технологических расчетах, особенно с применением ЭВМ, удобно использовать следующие аппроксимационные уравнения для функции z = f(Рпр, Тпр). Для углеводородной составляющей газа в области давлений и температур, наиболее часто встречающихся в практике эксплуатации нефтяных скважин (Р = 0 - 20 Мпа, Т = 273 - 355 °К):
1) при 
(18)
2) при 
(19)
3) при 
(20)
Для азота в интервале давлений Р = 0 - 20 Мпа и температур Т=280 -380 °К:
. (21)
Для расчета плотности газа и его объема при данных термодинамических условиях (Р, Т), отличных от нормальных или стандартных (когда z = zo = 1), используется уравнение состояния (13), из которого следуют соотношения:
, (22)
, (23)
где Vо (Vст),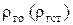 
- объем и плотность газа при нормальных или стандартных условиях [ Ро, То (Тст) ].