Данный подход к представлению классов объектов и отношений между ними базируется на использовании понятий исчисления предикатов. Суть заключается в следующем: взаимосвязи между различными объектами описываются с помощью предикатов. Если Р есть n -местная предикатная переменная, а х 1, х 2,..., хn – предметные переменные (аргументы предиката), то, по определению, выражение есть атомарная (элементарная) формула. Содержательно эта формула означает высказывание, гласящее, что объекты х 1, х 2,..., хn связаны отношением Р.
Порядок следования аргументов должен всегда задаваться в соответствии с интерпретацией предиката, принятой для моделирования ПО при разработке информационной системы, т.е. разработчик должен принять решение о фиксированном, приемлемом для интерпретации порядке и неукоснительно соблюдать его в системе при работе с такими данными.
Например, факт «Петров работает программистом» можно представить следующим образом:
Работает (Петров, Программист)
Причем теперь в системе все предикаты такого типа должны в списке аргументов на первом месте содержать фамилию служащего, а на втором месте – название должности, например:
Работает (Иванов, Лаборант)
Работает (Кузнецов, Слесарь) и т.п.
В приведенных примерах факты выражают единичные отношения, указанные слева от скобок, и перечисленные в скобках объекты, связанные данным отношением. Подобные структуры используют при моделировании для формирования основных предложений исчисления предикатов.
Используемые в исчислении предикатов логические выражения, называемые высказываниями, должны иметь значения либо истина, либо ложь.
В высказывании, записанном в нотации исчисления предикатов, некоторый объект может быть представлен как КОНСТАНТА, т.е. как конкретный индивидуум или класс индивидуумов, или как ПЕРЕМЕННАЯ, в результате чего конкретный индивидуум или класс индивидуумов остаются незаданными, например:
Является (X, Специалист по ЭВМ).
Одна из возможных интерпретаций этого предиката может быть такой: имеется некоторый объект X, который является специалистом по ЭВМ.
Когда переменной ставится в соответствии определенное имя некоторого объекта (т.е. некоторой константы), то говорят, что происходит порождение экземпляра этой переменной.
Высказывания, состоящие из предиката и связанных с ним аргументов, называются элементарными. Элементарные высказывания могут объединяться в сложные высказывания логическими связками:
И (and, Ù, &),
ИЛИ (or, Ú),
НЕ (not, Ø),
ИМПЛИКАЦИЯ (®).
Импликация читается как:
ЕСЛИ..., ТО....
Для того чтобы в исчислении предикатов можно было манипулировать переменными, введены дополнительные структуры – кванторы. Кванторы служат для указания меры, в какой экземпляры переменных должны быть истинны, чтобы высказывание в целом тоже было истинным:
" – квантор общности; $ – квантор существования.
Например, пользуясь кванторами, предложение «все специалисты по ЭВМ являются операторами» можно представить следующим образом:
("X)(Специалист по ЭВМ (X) ® ОПЕРАТОР (X)),
а предложение «некоторые специалисты по ЭВМ являются операторами»:
($Х)(Специалист по ЭВМ (X) ® ОПЕРАТОР (X)).
Кванторы общности и кванторы существования могут перемежаться в пределах одного и того же выражения. В этом случае порядок, в соответствии с которым вводятся квантифицируемые переменные, может влиять на смысл высказывания. Например, утверждение
("X)($Y) (Служащий (X) ® Руководит (Y, X))
может быть интерпретировано как «каждым служащим X руководит некоторое лицо Y». А утверждению
($Y)("X) (Служащий (X) ® Руководит (Y, X))
соответствует интерпретация «есть такое лицо Y, которое руководит всеми».
Конструирование сложных высказываний из элементарных с помощью логических связок и кванторов подчиняется определенным правилам, называемым правилами вывода. По правилам вывода можно из исходных, так называемых, правильно построенных формул (ППФ), строить новые правильно построенные формулы. Рассмотрим определение ППФ (далее будем говорить логическая формула).
1. Атомарный предикат является логической формулой.
2. Если А, В – логические формулы, то А Ù В, A Ú В,ù А, ù В, А ® В, В ® А также являются логическими формулами.
3. Если С (Х)– логическая формула, то и ("X)C(X), и ($Х) С(Х) так же являются логическими формулами.
4. Все формулы, полученные повторением конечного числа раз формул 1,2, и 3, являются логическими формулами.
С помощью правил вывода в логике предикатов можно из заранее заданных посылок вывести заключение. Сам вывод представляет собой процедуру, которая из заданной исходной группы выражений выводит отличное от них некоторое другое выражение. Использование только правил вывода гарантирует, что если группа выражений, образующая посылку, является истиной, то и полученное выражение также будет истиной.
Рассмотрим некоторые правила вывода.
1. Из двух логических формул А и А ® В выводится новая логическая формула В (Modus ponens). Для описания правил вывода во многих случаях используется нотация, когда над чертой записывается группа выражений, выступающих в качестве посылки, а под чертой записывается выражение, которое из них выводится:
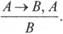
Например: «Если моя программа правильна, то она будет работать; моя программа правильна; следовательно, она будет работать». 2. Modus tollens (отрицательный способ рассуждений):
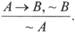
Например: «Если моя программа правильна, то она будет работать; моя программа не будет работать; следовательно, она неправильна».
3. Двойное отрицание:
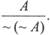
Например: «Моя программа работала; следовательно, моя программа не не работала».
4. Введение конъюнкции:
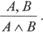
Например: «Моя программа работала, она правильна; следовательно, моя программа работала и она правильна».
5. Заключение истинности суждения независимо от посылки:
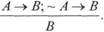
Например: «Если моя программа правильна, то она будет работать; если моя программа неправильна, то она будет работать; моя программа будет работать».
6. Специализация. Она означает, что если некоторому классу объектов присуще какое-либо свойство, то любой объект этого класса будет обладать этим же свойством:
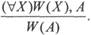
Например: «Все предметы, являющиеся ЭВМ, надежны; IBM PC -ЭВМ; следовательно, IBM PC надежна».
Правила вывода, которые из известных выражений выводят некоторое новое выражение, называют правилами дедуктивных выводов.
При использовании логики предикатов для описания ПО необходимо установить соответствие между понятиями описываемой ПО и предикатными формулами. Для этого необходимо выполнить следующее:
1) установить соответствие между константами логики предикатов и сущностями описываемой ПО (в качестве констант выступают имена сущностей);
2) установить соответствие между атомарными предикатами и отношениями, между сущностями, имеющими место в ПО;
3) выполнить описание функциональных отношений ПО с помощью формул логики предикатов;
4) задать значения истина или ложь в зависимости от выполнения или невыполнения отношений ПО, описанных логическими формулами.
Пример. БД представлена совокупностью трех фактов:
1: Руководит (Петров, Иванов) – интерпретация: Петров руководит Ивановым;
2: Руководит (Иванов, Кузнецов) – интерпретация: Иванов руководит Кузнецовым;
3: Руководит (Кузнецов, Яковлев) – интерпретация; Кузнецов руководит Яковлевым.
Эти факты истинны, поскольку имеют место в данной ПО, и потому их представляют в базе данных.
Далее описывают два прикладных правила (т.е. функциональных отношения), которые имеют место в рассматриваемой ПО.
Правило 1: "(X, Y) (Руководит (X, Y) ® Отчитывается (Y, X)) – интерпретация: «Для всех значений X и Y, если X руководит Y, то Y отчитывается перед X».
Правило 2: "(X, Y, Т) (Руководит (X, Y) Ù Отчитывается (Т, Y) ® Отчитывается (Т, X)), где X, Y, Т – переменные; интерпретация: «Для всех значений X, Y, Т, если X руководит Y и Т отчитывается перед Y, то Т отчитывается перед X».
Теперь посмотрим, как в такой модели можно обрабатывать запросы пользователей. Например, поступает следующий запрос: «Проверить, имеет ли место в ПО факт «Яковлев отчитывается перед Ивановым» (т.е. иначе сделать заключение, что «Яковлев отчитывается перед Ивановым».
Итак, в данной базе данных непосредственно такого факта нет. Однако предикат, описывающий интересующее нас отношение, встречается в правилах 1 и 2. Применим правило 1 к факту 3. Выполнив подстановку значения констант из факта 3 на позиции соответствующих переменных в правиле 1, получим следующую логическую формулу:
Руководит (Кузнецов, Яковлев) ® Отчитывается (Яковлев, Кузнецов).
Применяя к ней и факту 3 правило вывода Modus ponens, получим логическую формулу
Отчитывается (Яковлев, Кузнецов),
описывающую тот факт, что Яковлев отчитывается перед Кузнецовым. Так как применялось правило вывода и исходные выражения были истинными, то, следовательно, и данное заключение является истинным. Итак, данный факт имеет место в данной ПО, хотя в явном виде он в базе и не представлен.
Применяя к этому факту (промежуточному результату) и факту 2 правило 2 и выполнив подстановку значений констант из фактов на позиции соответствующих переменных в правиле 2, получим следующую логическую формулу:
Руководит (Иванов, Кузнецов) Ù Отчитывается (Яковлев, Кузнецов) ® Отчитывается (Яковлев, Иванов).
Применяя к факту 2 и к факту (Отчитывается Яковлев, Кузнецов) правило вывода «введение конъюнкции», получим логическую формулу Руководит (Иванов, Кузнецов) Ù Отчитывается (Яковлев, Кузнецов).
Применяя к ней и к формуле
Руководит (Иванов, Кузнецов) Ù Отчитывается (Яковлев, Кузнецов) ® Отчитывается (Яковлев, Иванов)
правило вывода Mondus ponens, получим логическую формулу
Отчитывается (Яковлев, Иванов),
описывающую тот факт, что Яковлев отчитывается перед Ивановым.
Так как применялось правило вывода и исходные посылки были истинными, то данное заключение является истинным. Теперь можно дать утвердительный ответ на запрос, действительно ли в ПО имеет место факт, что Яковлев отчитывается перед Ивановым.
Системы продукций
Этот класс моделей при представлении в системе знаний базируется на использовании так называемых продукций. Продукция – это правило вида:
ЕСЛИ левая – часть – правила, ТО – правая – часть – правила.
Если левая часть правила является посылкой, а правая – заключением, то имеют дело с элементарным логическим актом (логической операцией).
Если левая часть правила является описанием ситуации, а правая – действия, то такая продукция характерна, например, для систем управления и т.п. Ясно, что подобного рода продукции можно применить в различных областях знания и сфер деятельности. Например, в медицинских системах левая часть продукции может выступать в качестве симптома заболевания, а правая – в качестве диагноза и т.п.
Отметим следующую особенность этого класса моделей. Значения каких-либо продукций могут входить в условия других, что приводит к образованию сложных цепочек, которые можно использовать для логического вывода. Имеющаяся в системе программа-планировщик может в этом случае выполнять логический вывод как прямой, от условий к заключительному факту, так и обратный – от заключительного факта. В последнем случае заключительный факт рассматривается как гипотеза, для которой необходимо сделать проверку – подтверждается эта гипотеза имеющимися в системе фактами, выступающими в качестве условий, или нет.
Системы продукции включают три основных компонента:
базу данных, содержащую множество фактов, описывающих ПО;
базу правил, состоящую из набора продукций – правил вывода, имеющих место в предметной области;
управляющую структуру (УС) (или, как ее еще называют программа-планировщик, интерпретатор), реализующую механизм логического вывода: УС имеет рабочую кратковременную память, в которой она реализует необходимые преобразования правил, соединение их в цепочки с целью получения логического вывода для конкретной решаемой задачи.
Заметим, что база правил и БД в совокупности образуют БЗ.
Факты в модели представляются в правой части правила продукции, т.е. как заключение без посылки.
Используя нотацию исчисления предикатов, продукцию ЕСЛИ А ТО В можно записать в виде A Ú В, и в этом случае база знаний системы описывается в виде совокупности предложений:

Управляющая структура является третьим необходимым компонентом процесса обработки знаний в данной модели. Она определяет порядок и последовательность применения правил. Основной задачей в модели систем продукций является проверка наличия в БЗ фактов, касающихся условной (левой) части правила.
Так как левая часть продукций может состоять из одного либо нескольких условий, соединенных связкой И, а в базе знаний может существовать несколько правил, из которых выводится одно и то же заключение, то всю систему продукций можно представить в виде графа И–ИЛИ. В самых нижних узлах этого графа будут располагаться факты, а в самых верхних – заключения, выводимые системой. Следовательно, вывод, получаемый системой продукций, можно представить в виде совокупности правил, поддерживающих заключение, и совокупности данных, на основании которых делается вывод. Таким образом, проблему вывода можно представить как проблему поиска пути на графе.
Варианты управляющих структур в реальных системах разнообразны. Есть УС, которые перебирают правила последовательно, т.е. работают по принципу: поочередно опробовать правила, которые заданы последовательным списком, пока одно из них не сработает; затем следовать к началу списка правил и начать процесс опробования сначала; процесс закончить при встрече оператора «стоп». Такая УС независима от ПО и является универсальной. Но правила в ней должны быть независимы от порядка расположения в базе.
Другой вариант – часть знаний о ПО переносят из базы знаний в УС, т.е., таким образом, модифицируют алгоритм УС, чтобы ускорить в базе поиск тех данных, которые релевантны запросу.
В реальных системах продукций зачастую возникает необходимость работы с нечеткой информацией. В этом случае заключение выводится с участием нечетких данных и с помощью специальной оценочной функции определяется степень нечеткости всего заключения.
Относительная простота механизма логического вывода, а также простота создания, понимания и модификации отдельных правил привели к широкому использованию этой модели представления знаний в ЭС.
Контрольные вопросы
1. Охарактеризуйте основные концепции, реализованные в СЕМС.
2. Приведите пример представления конкретной ситуации с помощью СЕМС.
3. Рассмотрите пример построения сети фреймов.
4. Приведите пример «сценария».
5. Приведите пример представления знаний с помощью логики предикатов.
6. Охарактеризуйте особенности моделей типа «системы продукций».