Лабораторная работа ЭВ.2.

ИНТЕРФЕРЕНЦИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН.

Кольца Ньютона

Цели работы

1) Наблюдение и изучение интерференции с помощью «колец Ньютона».

2) Определение радиуса кривизны линзы, создающей кольца Ньютона.

Теоретическое введение

Колеблющимися величинами в электромагнитной волне являются векторынапряженностейэлектрического Е и магнитного Н полей. В монохроматической волне (например, в световой волне, прошедшей через светофильтр) эти ве­личины в каждой точке пространства совершают гармонические коле­бания, т. е. изменяются с течением времени по гармоническому (синусоидальному) закону. Количество полных колебаний за одну секунду называется частотой волны (частòты видимых световых волн лежат в диапазоне — Гц). Если взять наугад две какие-ни­будь точки в волне, то колебания в этих точках будут, вообще го­воря, асинхронными, т.е. одно из них будет запаздывать по от­ношению к другому (иначе говоря, их фазы различны). Однако в волне на одинаковых расстояниях друг от друга расположены точки, колебания в которых синхронны (нахо­дятся в одной фазе). Минимальное расстояние между двумя такими точками называется длиной волны. Длина волны , частота и скорость распространения волны с свя­заны соотношением

(1)

Величина , характеризующая длительность одного полного колебания, называется периодом колебаний. Соотношение (1) можно переписать так: . Значит, длина волны — это расстояние, который волна проходит за один период.

Как и волны любой иной природы, электромагнитные волны (в частности, свет) способны интерферировать. Интерфе­ренцией называется явление взаимного усилия или ослабления двух или большего числа волн при их наложении друг на друга. Усиление возникает, если в точке, где смешиваются волны, колебания находятся в фазе, при этом на «горбы» одной волны накладываются горбы же другой. Ослабление возникает, если волны находятся в противофазе, в этом случае на горбы одной приходятся «впадины» другой. Ин­терферировать друг с другом могут только когерентные волны, т. е. волны, характеризующиеся постоянной во времени разностью фаз. (В случае электромагнитных плоскополяризованных волн для интерференции, помимо когерентности, необходимо, чтобы совпадали плоскости поляризации интерферирующих волн). Когерентные волны обычно получают, разделяя излучение одного монохроматического источни­ка на различные лучи. Если «предыстории» этих лучей до смешения друг с дру­гом различны (например, если лучи до смешения проходят различные расстояния), то в точку смешения они приходят в разных фазах. В точке смешения интерференция приводит к взаимному ослаблению, если разность пройденных лучами расстояний (называемая геометрической разностью хо­да) выражается нечетным числом отрезков длиной в , т. е. нечетным числом полуволн. В этом случае горб од­ной волны встречается с впадиной другой. Если же разность хода равна четному числу полуволн, то, как указывалось, на горб одной волны накладывается горб другой, приводя к увеличениюамплитуды колебаний.

Разность фаз двух разделенных лучей образуется не только из-за несовпадения проходимых ими расстояний. Так, при отражении от оптически более плотной среды (т.е. среды с бòльшим показа­телем преломления) световой луч «теряет» полволны; это эквива­лентно увеличению (или уменьшению) его фактического пути на . Поэтому результат интерференции волн определяется не просто геометрической разностью хода, а итоговой — оптической разностью хода, которая в данном случае представляет собой сумму геометрической разности хода (выраженной в числе полуволн) и числа «потерянных» полуволн.

Рассмотрим следующий пример интерференции. Пусть монохроматическая световая волна падает на плоскопараллельную прозрачную стеклянную пластину, расположенную на высоте h над отражающей поверхностью (см. рис. 1). Предположим, что отражением от верхней поверхности пластины можно пренебречь и что существенно только отражение от ее нижнего края. Тогда каждый луч, достигнув нижней поверхности пластины, будет раздваиваться: одна часть волны отразится от ниж­него края, а часть пройдет дальше, отразится от расположенного ниже зеркала и, вернувшись обратно, сольется с первой «половиной» волны (для наглядности идущие вверх лучи изображены на рисунке правее породившего их направленного вниз луча). Таким обра­зом, в точке, помеченной на рисунке крестиком, происходит смеше­ние двух волн, причем вторая проходит дополнительный путь . Геометрическая разность хода, выраженная в числе полуволн, по­этому равна . Однако эта же волна, кроме того, теряет полволны за счет отражения от оптически более плотной среды. Следователь­но, оптическая разность хода d (выраженная в числе полуволн) окажется на единицу больше: Если оптическая разность хода будет нечетным числом (например, 2 n + 1, где n = 0, 1, 2,...), то два луча взаимно ослабят друг друга, и сверху пла­стина будет казаться темной. Если же оптическая разность хода бу­дет четной, то лучи, наоборот, усилят друг друга, и пластина по­кажется сверху светлой. Запомним из этого рассуждения, что усло­вие взаимного ослабления двух лучей имеет вид:

. (2)

Рассуждения в только что разобранном примере требуют корректирующих пояснений. Как уже указывалось колеблющимися величинами в электромагнитной волне являются векторы Е и Н, образующие с волновым вектором k (и с вектором Пойнтинга S=[EH] для плотности потока электромагнитной энергии) правую тройку. Так как интерференция происходит между волнами, отраженными от верхней и нижней поверхностей воздушной прослойки, то для вычисления разности фаз нужно иметь в виду, как правильно указывалось, помимо геометрической разности хода внутри воздушной прослойки, еще и изменение фаз электрического и магнитного векторов при отражении на границах стекло — воздух и воздух — стекло. Это изменение приводит как для Е, так и для Н к дополнительной разности фаз, равной . При этом для Е первое отражение происходит без изменения фазы, а второе с изменением фазы на , а для вектора Н — наоборот. Такое поведение Е и Н награницах раздела сред обеспечивает «разворот» падающих волн, их преобразование в отраженные. Действительно, изменение фазы на у любого из векторов поля означает, что вектор переориентирован в противоположном направлении. При этом, если другой из векторов поля сохраняет прежнее направление, то чтобы тройка векторов оставалась правой, обязан изменить направление на обратное волновой вектор k.

Теперь нетрудно разобраться и с кольцами Ньютона. Предста­вим себе, что на зеркальной плоской поверхности лежит линза с большим радиусом кривизны R (рис. 2). Пусть эта линза освещается сверху монохроматическим светом. Ввиду того, что R, очень велико, нижний край линзы практически параллелен зеркалу, и на любом не очень большом участке зеркала мы фактически будем иметь дело с разобранным ранее случаем плоскопараллелъной пластины. Правда, теперь на разных расстояниях от центра линзы величина ока­жется различной, так что где-то будут выполнены условия ослабле­ния лучей, а где-то — условия усиления. Рассматривая линзу свер­ху, мы увидим поэтому систему чередующихся темных и светлых ко­лец (см. рис. 3) с темным кругом в центре. Это и есть кольца Ньютона.

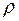Чтобы получить формулу для радиуса n -го кольца Ньютона, нужно найти зависимость величины от расстояния до центра линзы. Находим из рис. 2

. (3)

Если 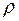мало по сравнению с R, то эту формулу можно упростить:

. (4)

Учитывая условие (2) минимума освещенности, получаем, что , и, следовательно, радиус n -го темного кольца Ньютона дается выражением . (5)

В рамках данной лабораторной работы это соотношение используется для определения радиуса R кривизны линзы по известной длине волны света и измеренной величине . Заметим, что радиус n -го светлого кольца Ньютона описывается доказываемой аналогично (5) формулой

.

Лабораторная установка представляет собой линзу, на которой установлены источник света и микроскоп, служащий для регистрации интерференционной картины колец Ньютона.

Интерференцию наблюдают в отраженном свете с помощью микро­-
скопа. Так как кольца, близкие к центру, имеют размытый характер, целесообразно проводить измерения радиусов колец более высокого порядка, начиная с 5-го кольца. Для большей точности измерений расчет радиуса линзы делают, измеряя радиусы двух колец Ньютона, далеко отстоящих друг от друга. Обозначая их порядковые номера через k и m (например, 10-е и 5-е или 15-е и 10-е), можно записать

Вычитая из первого равенства второе, получаем

.

Таким образом, расчет радиуса линзы следует вести по формуле

(6)

Порядок выполнения работы

1.Ознакомиться с микроскопом и отсчетным устройством.

2. Добившись четкой интерференционной картины и появления в центре темного пятна, совместить крест нитей окуляра микроскопа с центром интерференционной картины.

3. Осторожно перемещая крест нитей влево, совместить его с
серединой ширины линии 5-го темного кольца. Отметить показания индикатора в таблице.

4. Измерить c 1-го по 10-е темные кольца, занося показания в таблицу .

5. Измерения повторить в обратном порядке от 10-го до 1-го кольца слева от центра . Это необходимо для уменьшения ошибки измерений. Определить

6. Повторить пп. 3 — 5 для 5 — 15-го колец справа от центра и . Рассчитать

№ коль-ца										R

7. Найти радиус каждого кольца
8. Используя расчетную формулу (6), определить радиус R лин- зы, найти его среднее значение и оценить погрешность измерений.

Таблица

Контрольные вопросы

1. Электромагнитные волны. Характеристики электромагнитных волн: длина волны λ, частота ν. Интенсивность электромагнитной волны.

2. Электромагнитные волны. Механизм электромагнитного волнового процесса, взаимосвязь полей.

3. Свойства электромагнитных волн: скорость с распространения в вакууме, поперечность.

4. Свойства электромагнитных волн: поляризация и ее виды.

5. Энергия электромагнитной волны. Вектор Пойнтинга (формула, физический смысл).

Литература

1. А. В. Астахов, Ю. М. Широков. Курс физики. М.: «Наука», 1980. Т. II. 359 с.

2. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1965. Т. 3. 238 с.

3. Д. В. Сивухин. Общий курс физики. Т.IV. Оптика. М.: «Наука», 1980. 752 с.

4. И. Е. Иродов. Волновые процессы. Основные законы. М.-СПб.: Физматлит, 1999. 254 с.