На дифракционной решетке

Цель работы

Определение длин волн ртутного спектра с помощью дифракционной решетки

Теоретическое введение

Дифракцией называют любые отклонения наблюдаемых законо­мерностей распространения света от законов геометрической оптики (согласно которым световые лучи распространяются прямолинейно). Дифракция свидетельствует о волновой природе света. Она становит­ся заметной, если длина световой волны сравнима по порядку величины с размерами препятствий, стоящих на ее пути. В этом случае свет как бы огибает препятствие. Если препятствия образуют регулярную структуру (например, систему большого количества равностоящих друг от друга параллельных щелей одинаковой ширины, т.е. так называемую дифракционную решет­ку), то на расположенном за препятствиями экране возникает харак­терная система чередующихся темных и светлых полос, именуемая дифракционной картиной. Дифракцию обычно наблюдают в монохроматическом (одно­цветном) свете, т.е. в свете с фиксированной длиной вол­ны.

Образование дифракционной картины вызвано интерференцией когерентных волн, пришедших к той или иной точке экрана по раз­личным траекториям. Поэтому, чтобы понять дальнейшее, необходимо ознакомиться с явлением интерференции, хотя бы в объеме теоретического введения к лабораторной работе ЭВ.2.

Для объяснения дифракции существен также принцип Гюйгенса-Френеля. Согласно этому принципу каждую точку световой волны можно рассматривать как источник новых волн (той же частоты), распро-страняющихся по всем направлениям. Форма волны во все последующие моменты времени, а также характер дифракционной картины трактуются как результат интерференции этих «вторичных волн». Вчастности, если две вторичные волны одинаковой интенсивности приходят в точку наблюдения, имея разность хода, равную нечетному числу полуволн, то эти волны взаимно гасят друг друга, Если же разность хода для этих вторичных лучей составляет четное число полуволн (т. е. целое число длин волн), то интенсивность волны в соответствующей точке удваивается.

Дифракционная решетка — это бесконечная система параллель­ных равноотстоящих друг от друга щелей ширины с. Если расстояние между соседними щелями равно a, то величина b = a + c называ­ется постоянной решетки (см. рис. 1).

Предположим, что на решетку (перпендикулярно к ней) падает монохроматическая волна. Оценим интенсивность излучения, исходящего от дифракционной решетки под углом .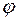

В описанных условиях интерференция между лучами, исходящими из разных точек одной и той же щели, гораздо менее существенна, чем интерференция между лучами, исходящими от разных щелей. По­этому будем учитывать только этот тип интерференции.

Разность хода между лучами, выходящими в направлении 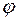от двух соседних щелей решетки, равна

(1)

Если эта разность хода в точности равна целому числу длин волн, т.е.

(2)

то результатом наложения лучей от соседних щелей является максимальная интенсивность; точнее говоря, в соответствующем направле­нии будет наблюдаться -й максимум. Таким образом, условие, определяющее -й максимум освещенности, имеет вид

. (3)

В данной работе дифракционная решетка является спектральным.прибором, Для наблюдения дифракционной картины используется опти­ческий прибор, называемый гониометром (ГС-5), который состоит из зрительной трубы, коллиматора и отсчетного устройства. Он содержит столик, на котором укреплена дифракционная решетка. Свет от источника направляется на решетку при помощи коллиматора, на конце которого, обращенном к источнику, имеется узкая верти­кальная щель. Ширина щели меняется с помощью специального винта. Щель находится в фокусе линзы. Лучи, пройдя линзу, падают на решетку параллельным пучком. Наблюдают дифракционное изображение через окуляр зрительной трубы. Поворачивая зрительную трубу, до­биваются совмещения вертикальной риски окуляра с интересующим дифракционным максимумом и делают отсчет по лимбу гониометра. Разность двух отсчетов слева и справа от белой линии дает угол 2 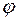. Зная период решетки b = 0,02 мм, по формуле

находят длины волн соответствующих линий спектра.

Порядок выполнения работы

1. Ознакомиться с гониометром. Включить ртутную лампу.

2. Поворачивая зрительную трубу, добиться совмещения окулярной риски с синей линией в спектре 1-го порядка слева от бе­лой центральной линии. Сделать отсчет по шкале лимба 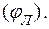Цена деления шкалы 20'.

3. Аналогично сделать измерения синей линии в спектрах 2-го и 3-го порядков. Данные заносить в табл. I.

Таблица 1

Цвет линии	Порядок спектра	Отсчеты			,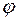
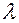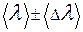
Синий
Зеленый
Желтый

4. Проделать п.п. 2, 3 для синей линии справа от центра дифракционной картины для спектров 1-го, 2-го и 3-го порядков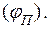

5. Пункты 2 4 повторить для зеленой и желтой линий спектра.

7. Рассчитать угол , найти длины волн измеренных линий.

8. Определить среднее значение каждой длины волны.

Контрольные вопросы

1.Цель работы.

2. Уравнения Максвелла.

3. Электромагнитные волны (механизм электромагнитного вол­нового процесса и его характеристики).

4. Свойства электромагнитных волн: скорость распространения в вакууме, поперечность, взаимосвязь полей.

5. Поляризация и виды поляризации электромагнитных волн.

6. Характеристики электромагнитных волн: импульс, энергия, интенсивность.

7. Интерференция (сущность явления).

8. Интерференция (условие реализации — когерентность, время
когерентности)

9. Дифракция (сущность явления).

10. Принцип Гюйгенса-Френеля.

11. Дифракция Фраунгофера на решетке.

12. Содержание лабораторных упражнений. Порядок и х выполнения.

Литература

1. А. В. Астахов, Ю. М. Широков. Курс физики. М.: «Наука», 1980. Т. II. 359 с.

2. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1965. Т. 3. 238 с.

3. Д. В. Сивухин. Общий курс физики. Т.IV. Оптика. М.: «Наука», 1980. 752 с.

4. И. Е. Иродов. Волновые процессы. Основные законы. М.-СПб.: Физматлит, 1999. 254 с.