Изучение поляризации света

Московский государственный горный университет

____________________________

Кафедра физики

ЛАБОРАТОРНЫЕ РАБОТЫ

ПО ФИЗИКЕ

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

( ОПИСАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ )

МОСКВА

 

 

Учебное пособие содержит описания лабораторных работ по теме «Электромагнитные волны», входящей в раздел физики «Колебания и волны». Основному тексту описания каждой работы предпослан теоретический материал, который включает краткое изложение сути изучаемого явления и представлен в объеме, достаточном для получения допуска к выполнению лабораторных работ. Применительно к каждой работе в пособии освещены экспериментальный метод исследования изучаемого явления, используемая аппаратура, даны указания о приемах наблюдений и методике измерений, изложены требования по обработке результатов измерений, приведен список литературы для более глубокого ознакомления с темой.

 

Учебно-методическое пособие подготовлено на кафедре физики МГГУ. Под редакцией Р.З. Муратова.

 

Авторский коллектив: Л.В. Мудрецова и Ф.В. Шапошников (ЭВ1), О.Б. Карпов и Л.В. Мудрецова (ЭВ2), Р.З. Муратов и А.Ф. Мухамедгалиева (ЭВ3), А.Ф. Мухамедгалиева и Д.Л. Широчин (ЭВ4).

 

В материально-технической реализации лабораторного комплекса участвовали сотрудники лаборатории (зав. лабораторией Л.В. Мудрецова).

 

 

Рецензент — проф. Е.Б. Черепецкая

 

 

ВВЕДЕНИЕ

Предлагаемое методическое пособие объединяет лабораторные работы, в которых изучаются свойства электромагнитных волн. Из обширного частотного диапазона (радиоволны, инфракрасное, видимое, ультрафиолетовое, рентгеновское и гамма-излучения), в котором существуют электромагнитные волны, в данных работах представлен только видимый свет (чему соответствуют длины волн, лежащие в диапазоне 400—760 нм). Так что фактически речь идет о работах, относящихся к оптике [1]. Положительное следствие этого — возможность наблюдать изучаемые явления в буквальном смысле воочию.

В трех из представленных в пособии работ изучаются интерференция и дифракция — явления, свойственные волновым полям любой природы (электромагнитным волнам произвольного диапазона, упругим волнам, волнам в плазме, квантовомеханическим волнам амплитуды вероятностей и т.д.). Впервые явление интерференции оптических волн (в форме возникновения разноцветной окраски тонких пленок) было обнаружено в XVII веке независимо Р. Бойлем и Р. Гуком. Как известно, интерференционная картина (а нередко и дифракционная картина) есть результат наложения (суперпозиции) когерентных волн, а ее истолкование опирается на анализ фазовых соотношений интерферирующих волн.

В случае плоскополяризованных электромагнитных волн, как обнаружили в 1816 г. Араго и Френель, помимо удовлетворения требуемым фазовым соотношениям интерферирующие волны должны быть поляризованы в одной плоскости. Юнг, узнавший об этом от Араго, в 1817 г. выдвинул предположение о поперечности световых колебаний. Поперечность и поляризация являются, таким образом, неотъемлемыми свойствами электромагнитных волн, изучению которых посвящена первая из лабораторных работ, представленных в данном методическом пособии.

 

 

Лабораторная работа ЭВ.1

 

ИЗУЧЕНИЕ ПОЛЯРИЗАЦИИ СВЕТА

Цели работы

1) Изучение явления поляризации света.

2) Экспериментальная проверка закона Малюса.

3) Измерение угла Брюстера.

 

Теоретическое введение

Поляризация свойственна только поперечным волнам. К их числу относятся и электромагнитные волны. Как известно, электромагнитная волна характеризуется двумя взаимно перпендикулярными колеблющимися векторами напряженностей электрического Е и магнитного Н полей, которые образуют с направлением распространения волны, т. е. с волновым вектором k, правую тройку. Выражение вектора Пойнтинга S=[EH], т. е. плотности потока электромагнитной энергии, через Е и Н, также указывает на поперечность электромагнитной волны (S параллелен k).

Если пространственная ориентация вектора напряженности электрического поля со временем не меняется или изменяется некоторым упорядоченным образом, то свет называется поляризованным. Если колебания вектора Е происходят в одной и той же плоскости, то волна называется плоскополяризованной (или линейно поляризованной), а сама эта плоскость, образуемая векторами Е и k, именуется плоскостью поляризации.

Обычные источники света испускают естественный свет, в котором напряженность электрического поля хаотически изменяет свое направление, оставаясь перпендикулярной к волновому вектору k. Существует также частично поляризованный свет, представляющий собой смесь естественного света с плоскополяризованным.

Плоскополяризованный свет можно получить из естественного, пропуская его через поляризатор. Этот прибор свободно пропускает волны, в которых вектор Е колеблется параллельно так называемой плоскости пропускания поляризатора, но задерживает волны с колебаниями вектора Е, перпендикулярными к этой плоскости.

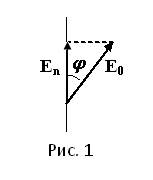
Если в падающей на поляризатор плоскополяризованной волне амплитуда вектора Е составляет угол φ с плоскостью пропускания поляризатора, то амплитуда прошедшей через поляризатор волны (см. рис. 1) равна

Е _п = Е_о cos φ. (1)

 

Поскольку интенсивность световой волны пропорциональна квадрату ее амплитуды , то интенсивность после поляризатора дается формулой

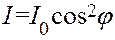,(2)

выражающей закон Малюса.

Рассмотрим наклонное (угол падения отличен от нуля) падение плоской электромагнитной волны на плоскую границу раздела двух однородных прозрачных сред (рис. 2). Плоскость, в которой лежат вектор n нормали к границе и волновой вектор k _пад падающей волны, называется плоскостью падения. В этой же плоскости находятся и волновые векторы k _отр отраженной и k _пр преломленной волн. Обсудим сначала случай, когда наклонно падает

		kотр

		Рис. 2
	kпр

плоскополяризованная волна. Нас интересует коэффициент отражения R, т. е. отношение среднего (по времени) отраженного от поверхности потока энергии к падающему потоку. Как следует из формул Френеля (так называются соотношения, выражающие амплитуды полей отраженной или преломленной волны через амплитуду Е падающей волны), коэффициент отражения R зависит от угла между плоскостью падения и плоскостью поляризации волны. Удобно различать два случая поляризации: 1) (при этом вектор Е перпендикулярен плоскости падения), 2) (вектор Е лежит в плоскости падения). Соответствующие коэффициенты отражения равны

 

 

(3)

 

Здесь — угол падения, — угол преломления, а индексные символы и отмечают случаи, когда поле Е соответственно перпендикулярно или параллельно плоскости падения (в общем случае вектор Е может быть разложен на указанные два направления). Замечательным свойством обладает отражение света, падающего под таким углом , при котором (отраженный и преломленный лучи при этом взаимно перпендикулярны). Обозначим это значение, называемое углом полной поляризации или углом Брюстера, посредством . Написав 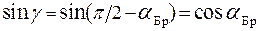и воспользовавшись законом преломления

,

получим

.(4)

 

Здесь и — показатели преломления сред (рис. 2).

При имеем и обращается в нуль. Поэтому при любом направлении поляризации света, падающего под этим углом, отраженный свет поляризован так, что электрическое поле в нем перпендикулярно к плоскости падения. Сказанное иллюстрирует рис. 2, где электрическое поле падающей волны представлено суммой двух взаимно перпендикулярных составляющих, из которых вектор лежит в плоскости падения (что отмечено на рисунке символом ), а перпендикулярен к плоскости падения (отмечено символом ). На аналогично ориентированные составляющие разложены и поля преломленной и отраженной волн.

Обращение в нуль при означает, что и при падении естественного света электрическое поле в отраженной волне будет перпендикулярно к плоскости падения: все компоненты с другой поляризацией при этом вообще не отразятся. Отметим, что в то время как отражение может приводить к полной поляризации естественного света, в преломленном свете полная поляризация не достигается ни при каком угле падения. Отметим также, что, как видно из формул (3), при всех углах падения (кроме и ) выполняется неравенство . Это означает, что в отраженной (кроме ) и преломленной волнах имеет место частичная поляризация.

Рис. 3