для применения которого нужно вычислить частные производные 2-го порядка в точке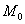 
Для компактности обычно используют следующие обозначения:
Если 
, то функция 
имеет экстремум в точке 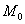, причём, если 
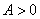, то это минимум, а если 
– то максимум.
Примечание: здесь также можно ориентироваться и на букву «цэ», т.к. неравенство выполняется только в том случае, если 
и 
– одного знака.
Если 
, то в точке 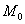нет экстремума.
Если же 
, то требуется дополнительное исследование, о котором загадочно умалчивают практически все источники. Впрочем, беспокоиться особо не нужно – встретите вряд ли.
В нашем примере все частные производные 2-го порядка равны константам:
а значит, соответствующим константам они равны и в частности в точке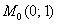 
:
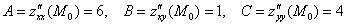
Таким образом: 
, следовательно, в точке 
есть экстремум, и так как 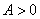, то это – минимум. Осталось его найти. Перепишем функцию 
, чтобы она была перед глазами, и ОЧЕНЬ внимательно проведём вычисления:
Надо сказать, момент весьма неприятный, поскольку здесь существует ненулевая вероятность запороть всё задание. Правда, в данном случае вычисления здОрово облегчил нулевой «икс».
Ответ: 
Признаюсь честно, привык я использовать значки 
, что не есть хорошо, т.к. они обычно используется для обозначения минимального и максимального значений функции. От чего вас и предостерегаю.
И справка для любознательных: поверхность 
представляет собой не что иное, как «подзашифорованный» эллиптический параболоид – весьма похожий на тот, который мы видели на 1-й картинке урока.
Пара разминочных примеров для самостоятельного решения:
Пример 2
Исследовать на экстремум функцию двух переменных
Пример 3
Исследовать на экстремум функцию двух переменных
Решение 3-го примера осложняется тем, что получается система нелинейных уравнений. Подумайте, что и откуда выгоднее выразить. Примерный образец чистового оформления задач в конце урока.
Когда я подбирал материалы к этой статье, то обнаружил у себя целую тьму подобных примеров (даже сам удивился) и поэтому рекомендую со всей ответственностью отнестись к предлагаемым заданиям.
Нередко приходится разбираться с двумя или даже бОльшим количествам стационарных точек. Типовая задача с экспонентой:
Пример 4
Исследовать функцию на экстремум
Решение: чтобы определить стационарные точки, найдем частные производные 1-го порядка и приравняем их к нулю. Техническая сложность дифференцирования состоит в применении правила 
, после чего, руководствуясь здравой логикой, нужно «загонять» слагаемые в одну скобку и по необходимости «наводить там порядок»:
На всякий пожарный проверим, что 
(тем более, находить всё равно придётся):
ОК
Составляем систему:
Поскольку экспоненты не могут равняться нулю, то их можно с чистой совестью убрать:
В подобных системах нужно проявить смекалку: где-то удаётся удачно выразить одну переменную через другую, где-то можно выделить полный квадрат, ну а у нас решение лежит на поверхности:
(к такому же результату приводит вычитание одного уравнения из другого )
Теперь подставляем соотношение 
в любое, например, во 2-е уравнение системы:
В результате получены 2 стационарные точки:
Не упущу возможности позанудствовать и напомнить о проверке – координаты найденных точек должны удовлетворять каждому уравнению системы.
Достаточное условие экстремума, как вы понимаете, нужно проверить для каждой точки отдельно. И в том, и в другом случае нам потребуются частные производные 2-го порядка:
Смешанная производная уже найдена:
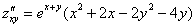
И, наконец, «двойная игрековая»:
...Это ещё не самый страх – пример я подобрал довольно гуманный =)
На очереди кропотливые вычисления:
1) Проверим выполнение достаточного условия экстремума для точки 
:
, значит, в точке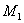 
нет экстремума.
2) Проверим выполнение достаточного условия экстремума для точки 
:
, значит, в точке 
существует экстремум, и поскольку 
, то это – максимум. Вспоминаем про функцию и НЕ ОШИБАЕМСЯ:
Ответ: 
О точке перевала в ответе не упоминаем. Зачем? Нас же просили провести исследование на экстремум.
От следующего задания тоже трудно отказаться – почти баян:
Пример 5
Исследовать функцию на экстремум
Краткое решение и ответ в конце урока
Время от времени посетители сайта просят меня включать в уроки задания и посложнее… ну что же, нашёлся тут интересный экземпляр: 
. Здесь придётся разрулить не самую простую систему и проверить на экстремум несколько стационарных точек. Чтобы не убивать интригу, в конце урока не будет ни решения, ни ответа =)
И специально для всех читателей mathprofi.ru, можно сказать, эксклюзивная задача:
Пример 6
Исследовать функцию на экстремум
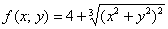
Решение начинается как обычно:
Но вот следующий шаг, казалось бы, сразу приводит к ответу об отсутствии экстремумов:
Система не имеет решений, поскольку единственная «подозрительная» точка 
обращает знаменатели в ноль, то есть функция 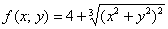– не дифференцируема в данной точке. Но неужели всё так просто? И действительно – ведь САМА-ТО функция там определена:
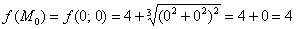
И более того, поверхность 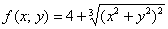непрерывна в точке (да и вообще в любой точке плоскости 
). Так почему же тут не может существовать минимум или максимум?
Сомнения не напрасны! По аналогии с похожим «плоским» случаем (см. Пример 8 урока Возрастание, убывание и экстремумы функции ) такая точка тоже считается стационарной и в ней тоже может быть экстремум!
Но здесь возникает второй камень преткновения. В знаменателях частных производных 2-го порядка (проверьте самостоятельно) находятся корни 
, что делает невозможным вычисление значений .
Как быть? В трудной ситуации всегда есть смысл проанализировать самое простое решение. А самое элементарное в экстремумах – это непосредственно их определения!
Рассмотрим достаточно малую 
-окрестность точки 
. Любую точку данной окрестности, отличную от , можно представить в виде 
, где значения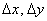 
не равны нулю одновременно и достаточно малы для того чтобы точка 
входила в эту окрестность.
Примечание: оба числа могут быть положительны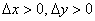 
, отрицательны 
, разных знаков: 
либо 
; и, кроме того, одно из них может равняться нулю (ещё 4 случая). Таким образом, обозначение 
действительно пригодно.
Вычислим значение функции в этой произвольной точке окрестности:
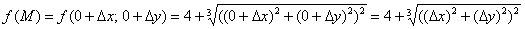
Так как 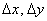не равны нулю одновременно, то корень 
будет хоть чуть-чуть, но больше нуля, а значит, 
. И вспоминая, что 
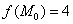, записываем очевидный факт: 
. Грубо говоря, в рассматриваемой окрестности значение 
«самое низкое».
Вывод: для точки нашлась -окрестность, в которой выполнено неравенство 
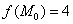, таким образом, – минимум по определению.
Нетрудно понять, что минимум глобальный. Геометрически поверхность представляет собой своеобразное пространственное остриё, а точнее – «шип».
Ответ: 
Представленное решение полностью корректно и полноценно! Более того, данный способ можно попытаться применить и в ситуации, когда достаточное условие экстремума не даёт ответа 
. Однако дело осложняется тем, что неравенство либо 
нужно обосновать для каждого из восьми случаев (см. Примечание), что реально осуществимо далеко не всегда. Зависит от функции.
И заключительный, не менее интересный параграф: