Плюс одно измерение. Рассмотрим функцию трёх переменных 
, внутреннюю точку 
её области определения и 
-окрестность данной точки, которая представляет собой шар с центром в точке 
радиуса 
.
Определение: если в некоторой -окрестности точки выполнено неравенство 
(
– точка -шара, отличная от ), то функция имеет минимум в точке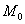 
; если же 
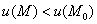– то максимум.
Вполне, кстати, понятное и не такое уж абстрактное определение.
Всё очень похоже. Если дифференцируемая функция имеет экстремум в точке , то обязательно выполняются условия 
. Но с другой стороны, если в какой-либо точке производные 1-го порядка равны нулю, то это ещё не значит, что там есть экстремум.
Алгоритм решения сохраняется прежним:
Пример 7
Найти экстремумы функции
Решение: переключаем передачу на частные производные функции трёх переменных:
Чтобы найти стационарные точки, составим и решим следующую систему:
Аккуратно расположим переменные в обычном порядке и, кроме того, разделим последнее уравнение на 2:
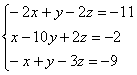
Систему можно решить методом Гаусса, нозачем такие сложности? Из 3-го уравнения выразим 
и подставим его в первые два уравнения:
Из 1-го уравнения выразим 
и подставим во 2-е уравнение:
Таким образом:
Таким образом, 
– стационарная точка. Здесь, напоминаю, не помешает подставить найденное решение 
в каждое уравнение исходной системы и убедиться в выполнении условий 
.
Проверка достаточного условия экстремума осуществляется несколько по-другому. Сначала нужно найти все частные производные 2-го порядка, вычислить их в точке 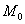и составить так называемую матрицу Гессе:
Да не пугайтесь вы так =) Данная матрица является симметричной (или симметрической). Это значит, что её элементы симметричны относительно главной диагонали, на которой в данном случае расположены «однобуквенные» частные производные 
. Уловили закономерность?
Далее нужно вычислить угловые миноры. Это определители, которые «разрастаются» из левого верхнего угла:
1) Если 
, то функция достигает минимума в точке .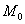
2) Если 
(так и только так!), то функция достигает максимума в точке .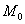
3) Если получилось что-то другое и при этом 
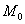, то – седловая точка. Здесь это уже во многом условное название.
4) Если 
, то признак не даёт ответа о характере точки .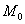
Внимательные читатели заметили, что эту схему в варианте «два на два» мы использовали и в предыдущем параграфе – только оформление «детское» было. Но не будем отвлекаться.
В нашем примере все производные 2-го порядка равны константам:
а значит, они равны константам и в точке 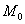. Составим матрицу Гессе:
и вычислим её угловые миноры:
Вывод: функция достигает максимума в точке 
.
Для удобства вычислений скопирую функцию:
Ответ: 
Аналогичное задание для закрепления материала:
Пример 8
Исследовать функцию на экстремум
Краткое решение и ответ рядом.
Рассмотренный алгоритм исследования распространяется и на функции бОльшего количества переменных. Я бы мог расписать его в общем виде, но заметная часть аудитории просто на дух не переносит общие формулы с нагромождением цифр и индексов. Поэтому разберём ещё случай функции 4 переменных, а дальше – будет понятно.
Чтобы исследовать на экстремум дифференцируемую функцию 
четырёх аргументов, нужно найти частные производные 1-го порядка и решить систему:
Предположим, что в результате решения найдена стационарная точка 
. Далее нужно найти частные производные 2-го порядка, вычислить их в точке 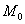и составить матрицу Гессе:
после чего вычислить её угловые миноры 
.
Если все миноры положительны, то в точке 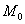– минимум, если знакочередуются в следующем порядке: 
(и именно в таком!), то в точке 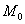– максимум. Если имеет место другой случай, но 
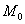, то – седловая точка; если же 
, то признак не даёт ответа о характере точки .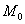
Ну и для совсем продвинутых читателей сообщу, что это есть не что иное, как проверка квадратичной формы полного дифференциала 2-го порядка на знакоопределённость методом Сильвестра (для функций 2, 3, 4 и бОльшего количества переменных).
Удачных вам исследований!
На следующих уроках мы познакомимся с условными экстремумами, задачей нахождения минимального и максимального значений функции, а также известнейшим приложением темы – Методом наименьших квадратов.
Как наберётесь сил – приходите ещё! =)
Решения и ответы:
Пример 2: Решение: найдём стационарные точки:
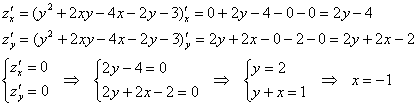
– стационарная точка.
Проверим выполнение достаточного условия экстремума:
, в частности:
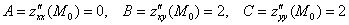
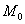, значит, в точке нет экстремума.
Ответ: экстремумы отсутствуют
Пример 3: Решение: найдём стационарные точки:
Из 1-го уравнения выразим: 
– подставим во 2-е уравнение: