ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ К КОНТРОЛЬНОЙ РАБОТЕ №4

Пример №1. Исследовать сходимость числового ряда .

Решение. Имеем , . Применяя признак Даламбера, вычислим

По признаку Даламбера данный ряд сходится.

Пример №2. Исследовать сходимость числового ряда .

Решение. Введем функцию , удовлетворяющую условию 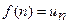, и исследуем сходимость по интегральному признаку. Для этого вычислим

Несобственный интеграл сходится, следовательно, сходится и данный ряд.

Пример №3. Найти интервал сходимости степенного ряда .

Решение. Составим ряд из модулей членов ряда и вычислим

По признаку Даламбера ряд сходится при , отсюда или . Следовательно, ряд абсолютно сходится при . Исследуем сходимость ряда в граничных точках. При и из данного ряда получаем соответственно числовые ряды и . Из интегрального признака сходимости следует, что эти ряды сходятся абсолютно, поэтому промежутком сходимости данного ряда является отрезок .

Пример №4. Вычислить определенный интеграл с точностью до 0.001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.

Решение. Пользуясь рядом Маклорена для , заменяя в нем на , имеем . Интегрируя в указанных пределах, получим

.

Четвертый член этого знакочередующегося сходящегося ряда меньше 0.001. Поэтому для вычисления искомого приближенного значения интеграла достаточно взять три первых члена ряда

.

Пример №5. Найти изображение по Лапласу функции

Решение. Предварительно преобразуем исходную функцию, воспользовавшись формулой . В результате получим . Воспользуемся изображением функций и . По теореме смещения получим

; .

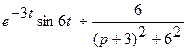Используя свойство линейности преобразования Лапласа, окончательно запишем

Пример №6. Найти функцию-оригинал для функции

.

Решение. Для отыскания функции-оригинала по данному изображению разложим функцию на простейшие дроби

 

.

 

Неизвестные находим методом неопределенных коэффициентов. Для этого приводим правую часть равенства к общему знаменателю

 

.

 

Из тождественного равенства дробей заключаем, что коэффициенты при соответствующих степенях в числителях дробей слева и справа должны быть равны. Это приводит к следующей системе уравнений для коэффициентов

Откуда получаем .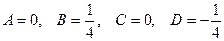

Тогда запишем

Для каждой из полученных дробей с помощью таблицы изображений основных элементарных функций легко установить функцию-оригинал

Откуда

Пример №7. Методом операционного исчисления найти частное решение дифференциального уравнения с начальными условиями .

Решение. Пусть решение имеет изображение , . Тогда по теореме о дифференцировании оригинала получим

.

Запишем изображение правой части исходного уравнения , тогда заданное дифференциальное уравнение примет вид

или

Функция является решением исходной задачи в изображении Лапласа. Найдем функцию-оригинал . Для этого разложим дробь на простейшие

Методом неопределенных коэффициентов получим , , . Для полученных дробей найдем функции-оригиналы

.

Окончательно решение дифференциального уравнения запишем в виде

Пример №8. Методом операционного исчисления найти решение системы дифференциальных уравнений

удовлетворяющее начальным условиям .

Решение. Обозначим , и напишем систему вспомогательных уравнений

Решая эту систему, находим

Здесь правые части уравнений разложены на простейшие дроби, как показано в примере 9. По изображениям находим функции-оригиналы, т. е. искомые решения системы

 

Пример №9. В партии из 20 изделий 5 изделий имеют скрытый дефект. Какова вероятность того, что из 4, взятых наугад изделий, 2 изделия будут дефектными?

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 4 изделия из 20, т.е. числу сочетаний из 20 элементов по 4 элемента (). Определяем число исходов, благоприятствующих событию А (среди 4 изделий 2 дефектных). Два дефектных изделия из 5 дефектных можно взять способами, при этом остальные 4-2=2 изделия должны быть недефектными; взять же 2 недефектных изделия из 20-5=15 недефектных изделий можно способами. Следовательно, число благоприятствующих исходов равно .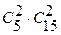

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

.

 

Пример №10. Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадет различное число очков (не равное шести).

Решение. Общее число элементарных исходов испытания равно числу сочетаний из шести элементов по три, т.е. .

Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равных шести) на гранях двух других костей, равно числу сочетаний из пяти элементов по два, т.е. .

Для вычисления числа сочетаний из элементов по воспользуемся формулой

.

Таким образом, искомая вероятность равна

.

Пример №11. Два стрелка производят по одному выстрелу по одной мишени. Первый попадает в мишень с вероятностью 0.8, второй – с вероятностью 0.6. Найти вероятность того, что: а) оба стрелка попадут в мишень, б) оба стрелка промахнутся, в) только один стрелок попадет, г) хотя бы один стрелок попадет в мишень.

Решение. Пусть событие А означает, что первый стрелок попал в мишень, событие В – попал второй. По условию

а) Пусть событие С – оба стрелка попали в мишень, тогда . Поэтому, учитывая независимость событий А и В, по теореме умножения вероятностей имеем

 

б) Перейдем к противоположным событиям, которые состоят в том, что первый стрелок промахнулся , второй стрелок промахнулся . Тогда событие означает, что оба стрелка промахнулись:

в) Событие Е – только один стрелок попал, можно представить в виде . События и несовместные. Поэтому, применяя теорему сложения вероятностей несовместных событий, получим

г) Вероятность появления хотя бы одного из совместных событий А, В равна разности между единицей и вероятностью произведения противоположных событий , . Пусть событие F – хотя бы один стрелок попал. Тогда

Пример №12. В первой урне 2 белых и 3 черных шара, во второй – 7 белых и 1 черный. Из первой урны во вторую переложили 2 шара, затем наудачу извлекли шар из второй урны. Найти вероятность того, что выбранный из второй урны шар – белый.

Решение. Если событие А может произойти только совместно с одним из событий , образующих полную группу несовместных событий (гипотез), то вероятность появления события определяется по формуле полной вероятности: , где - вероятность гипотезы , - условная вероятность события при этой гипотезе.

Вероятность извлечения белого шара из второй урны после добавления двух шаров из первой урны зависит от состава шаров (по цвету) в этой урне. При этом возможны следующие гипотезы:

- из первой урны во вторую переложены два белых шара,

- из первой урны во вторую переложен один белый и один черный шар,

- из первой урны во вторую переложены два черных шара.

Найдем вероятности этих гипотез. Вероятность каждой гипотезы связана с вероятностью извлечения соответствующих шаров из первой урны. Тогда получим

Пусть А – событие, состоящее в извлечении белого шара из второй урны, если предварительно имела место одна из гипотез . Условные вероятности события А будут равны

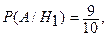
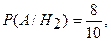
По формуле полной вероятности найдем вероятность извлечения белого шара из второй урны

Пример №13. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0.3, для второго - 0.5, для третьего – 0.8. Мишень не поражена. Найти вероятность, что выстрелы произведены первым стрелком.

Решение. Если вероятности гипотез до опыта были , а в результате опыта появилось событие А, то условная вероятность с учетом появления события А вычисляется по формуле Бейеса

.

Возможны три гипотезы: - на линию огня вызван первый стрелок; - на линию огня вызван второй стрелок; - на линию огня вызван третий стрелок. Так как вызов на линию огня любого стрелка равновозможен, то вероятности этих гипотез до опыта .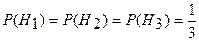

В результате опыта наблюдалось событие А – после произведенных двух выстрелов мишень не поражена. Условные вероятности этого события

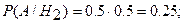
По формуле Бейеса, для частного случая, когда вероятности гипотез до опыта равны между собой, находим вероятность гипотезы после опыта

Пример №14. Найти вероятность того, что в пяти независимых испытаниях событие появится: а) ровно 3 раза, б) не менее трех раз, в) не более трех раз, г) хотя бы один раз, если в каждом испытании вероятность появления этого события .

Решение. Так как число испытаний невелико, то для вычисления искомой вероятности воспользуемся формулой Бернулли , где - число сочетаний из n элементов по k, . В рассматриваемом случае:

а) вероятность появления события ровно 3 раза в 5 испытаниях

б) вероятность появления события не менее трех раз в 5 испытаниях

в) вероятность появления события не более 3 раз в 5 испытаниях

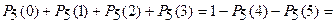
г) вероятность появления события хотя бы один раз в 5 испытаниях

 

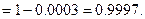
При решении б) - г) использована теорема сложения вероятностей несовместных событий, а при решении в), г) – понятие противоположных событий, сумма вероятностей которых равна 1.

Пример №15. Дана плотность распределения случайной величины Х. Найти параметр , функцию распределения случайной величины, математическое ожидание , дисперсию , вероятность выполнения неравенства

Решение. Для определения параметра воспользуемся основным свойством плотности распределения . Так как при плотность распределения равна нулю, то интеграл примет вид или откуда

Функция распределения связана с функцией плотности соотношением .

Отсюда получим

Математическое ожидание и дисперсию определим по формулам

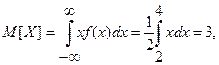
Вероятность выполнения неравенства определим по формуле

 

Пример №16. Заданы математическое ожидание и среднеквадратическое отклонение нормально распределенной случайной величины. Требуется:

1) написать плотность распределения вероятностей и схематично построить ее график;

2) найти вероятность того, что примет значение из интервала , если .

Решение. 1) Так как случайная величина имеет нормальное распределение, то ее плотность имеет вид:

.

Тогда

.

 

График функции 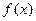называется кривой Гаусса и имеет вид (рисунок).

2) Вероятность попадания значений нормально распределенной случайной величины в интервал определяется формулой

где - функция Лапласа:

.

Учитывая то, что функция Лапласа является нечетной и используя таблицу значений функции , получим

.

Пример №17. Масса пойманной рыбы подчиняется нормальному закону с параметрами: , г. Найти вероятность того, что масса одной рыбы составит от 300г до 425г.

Решение. Для решения задачи воспользуемся формулой

где 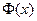- функция Лапласа и .

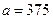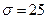Полагая в ней г, г, , получим

ПРИЛОЖЕНИЕ 1

Разложения в степенные ряды функций

.

ПРИЛОЖЕНИЕ 2

Таблица изображений основных элементарных функций

 

№	при
1.
2.
3.
4.
5.
6.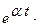
7.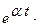
8.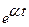
9.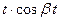
10.

ПРИЛОЖЕНИЕ 3

Таблица значений функции .

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09	0.0000 0.0040 0.0080 0.0120 0.0160 0.0199 0.0239 0.0279 0.0319 0.0359	0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19	0.0398 0.0438 0.0478 0.0517 0.0557 0.0596 0.0636 0.0675 0.0714 0.0753	0.20 0.21 0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29	0.0793 0.0832 0.0871 0.0910 0.0948 0.0987 0.1026 0.1064 0.1103 0.1141	0.30 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39	0.1179 0.1217 0.1255 0.1293 0.1331 0.1368 0.1406 0.1443 0.1480 0.1517
0.40 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49	0.1554 0.1591 0.1628 0.1664 0.1700 0.1736 0.1772 0.1808 0.1844 0.1879	0.50 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59	0.1915 0.1950 0.1985 0.2019 0.2054 0.2088 0.2123 0.2157 0.2190 0.2224	0.60 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69	0.2257 0.2291 0.2324 0.2357 0.2389 0.2422 0.2454 0.2486 0.2517 0.2549	0.70 0.71 0.72 0.73 0.74 0.75 0.76 0.77 0.78 0.79	0.2580 0.2611 0.2642 0.2673 0.2703 0.2734 0.2764 0.2794 0.2823 0.2852
0.80 0.81 0.82 0.83 0.84 0.85	0.2881 0.2910 0.2939 0.2967 0.2995 0.3023	0.90 0.91 0.92 0.93 0.94 0.95	0.3159 0.3186 0.3212 0.3238 0.3264 0.3289	1.00 1.01 1.02 1.03 1.04 1.05	0.3413 0.3438 0.3461 0.3485 0.3508 0.3531	1.10 1.11 1.12 1.13 1.14 1.15	0.3643 0.3665 0.3686 0.3708 0.3729 0.3749

Продолжение прил. 3

0.86 0.87 0.88 0.89	0.3051 0.3078 0.3106 0.3133	0.96 0.97 0.98 0.99	0.3315 0.3340 0.3365 0.3389	1.06 1.07 1.08 1.09	0.3554 0.3577 0.3599 0.3621	1.16 1.17 1.18 1.19	0.3770 0.3790 0.3810 0.3830
1.20 1.21 1.22 1.23 1.24 1.25 1.26 1.27 1.28 1.29	0.3849 0.3869 0.3888 0.3907 0.3925 0.3944 0.3962 0.3980 0.3997 0.4015	1.30 1.31 1.32 1.33 1.34 1.35 1.36 1.37 1.38 1.39	0.4032 0.4049 0.4066 0.4082 0.4099 0.4115 0.4131 0.4147 0.4162 0.4177	1.40 1.41 1.42 1.43 1.44 1.45 1.46 1.47 1.48 1.49	0.4192 0.4207 0.4222 0.4236 0.4251 0.4265 0.4279 0.4292 0.4306 0.4319	1.50 1.51 1.52 1.53 1.54 1.55 1.56 1.57 1.58 1.59	0.4332 0.4345 0.4357 0.4370 0.4382 0.4394 0.4406 0.4418 0.4429 0.4441
1.60 1.61 1.62 1.63 1.64 1.65 1.66 1.67 1.68 1.69	0.4452 0.4463 0.4474 0.4484 0.4495 0.4505 0.4515 0.4525 0.4535 0.4545	1.70 1.71 1.72 1.73 1.74 1.75 1.76 1.77 1.78 1.79	0.4554 0.4564 0.4573 0.4582 0.4591 0.4599 0.4608 0.4616 0.4625 0.4633	1.80 1.81 1.82 1.83 1.84 1.85 1.86 1.87 1.88 1.89	0.4641 0.4649 0.4656 0.4664 0.4671 0.4678 0.4686 0.4693 0.4699 0.4706	1.90 1.91 1.92 1.93 1.94 1.95 1.96 1.97 1.98 1.99	0.4713 0.4719 0.4726 0.4732 0.4738 0.4744 0.4750 0.4756 0.4761 0.4767
2.00 2.02 2.04 2.06 2.08 2.10 2.12	0.4772 0.4783 0.4793 0.4803 0.4812 0.4821 0.4830	2.20 2.22 2.24 2.26 2.28 2.30 2.32	0.4861 0.4868 0.4875 0.4881 0.4887 0.4893 0.4898	2.40 2.42 2.44 2.46 2.48 2.50 2.52	0.4918 0.4922 0.4927 0.4931 0.4934 0.4938 0.4941	2.60 2.62 2.64 2.66 2.68 2.70 2.72	0.4953 0.4956 0.4959 0.4961 0.4963 0.4965 0.4967

Окончание прил. 3

2.14 2.16 2.18	0.4838 0.4846 0.4854	2.34 2.36 2.38	0.4904 0.4909 0.4913	2.54 2.56 2.58	0.4945 0.4948 0.4951	2.74 2.76 2.78	0.4969 0.4971 0.4973
2.80 2.82 2.84 2.86 2.88 2.90 2.92 2.94 2.96 2.98	0.4974 0.4976 0.4977 0.4979 0.4980 0.4981 0.4982 0.4984 0.4985 0.4986	3.00 3.20 3.40 3.60 3.80 4.00 4.50 5.00	0.4986 0.4993 0.4996 0.4998 0.4999 0.4999 0.4999 0.4999