Анализ описанных выше моделей (1) и (2) выполняется при допущении, что все параметры и коэффициенты положительны (некоторые в частных случаях принимаются равными нулю) и не зависят от времени. Исследование систем уравнений начинаем с определения точек стационарных состояний, их типа и устойчивости. Модель (1) в общем случае имеет три особые точки, координаты которых определяются формулами:

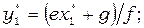
 (3)
(3)
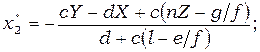
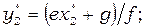
 (4)
(4)


 (5)
(5)
В частном случае, при  , в системе могут быть две особые точки. Тип и устойчивость точек определяется, как обычно, характеристическим уравнением для линеаризованной в окрестности этих точек системы.
, в системе могут быть две особые точки. Тип и устойчивость точек определяется, как обычно, характеристическим уравнением для линеаризованной в окрестности этих точек системы.
Система (1) диссипативна при условии:
 ,
,
которое выполняется всегда при положительных а и с. Следовательно, имеется предположение о возможности существования гетероклинических контуров, определяющих вид траекторий в фазовом пространстве.
Уравнения (1) и (2) исследовались численно методом Рунге-Кутта с переменным шагом и точностью  .
.
Зафиксируем константы модели (1), как указано в табл.1. Рассматривая коэффициенты d, e, f, k, l, m, n в качестве бифуркационных параметров, можем обнаружить все основные виды решений, характерных для трехмерных автономных нелинейных систем: стационарное состояние, предельный цикл, хаотический аттрактор и другие типы циклов различной периодичности. Например, на рис.2 и 3 представлены хаотический аттрактор, а также циклы типа  и
и  (в терминологии, принятой в работе [4]).
(в терминологии, принятой в работе [4]).
Таблица 1
Параметры модели макросистемы 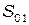
| a | b | c | d | e | f | g |
| 0.2 | 2.5 | 0.3 | 1.535 | |||
| k | l | m | n | X | Y | Z |
 а
а
 б
б
|  в
в
|
Рис.2. Проекции хаотического аттрактора (параметры соответствуют табл.1)
в координатах: а – z(y); б – x(z)

| 
|
а б
Рис.3. Циклы типа  и
и  при d = 2, e = 0.5, k = m = 0.5, l = n = 1
при d = 2, e = 0.5, k = m = 0.5, l = n = 1
(остальные параметры как в табл.1): а – f = 21; б – f = 10
Предположение о возможности существования гетероклинического контура косвенно подтверждается видом аттрактора (рис.4), полученного в системе (1) с параметрами, заданными в табл.2. На рис.4, б приведена зависимость z(t), которая свидетельствует о существовании так называемых контрастных структур и пограничного слоя [5] в решениях модели. Эти особенности являются неслучайными, так как при заданных в табл.2 параметрах система стремится к сингулярно возмущенной задаче, что и является, по-видимому, источником подобных эффектов. Зависимость z(t) весьма напоминает при этом некоторую стратегию управления запасами, что придает модели (1) практическую привлекательность.
Таблица 2
Параметры модели макросистемы  для случая
для случая
Контрастных структур
| a | b | c | d | e | f | g |
| 0.23 | 2.937 | 72,1 | 1.532 | 14,9 | ||
| k | l | m | n | X | Y | Z |
| 0.49 |
 а
а
 б
б
|  в
в
|
Рис.4. Проекция аттрактора (а, отмечены особые точки) с контрастными структурами и погранслоем (б)
К сожалению, в рамках данной статьи невозможно привести все найденные виды решений, исследование которых в настоящий момент находится тем не менее на начальной стадии.
Система (2) может иметь различное, в зависимости от числа действительных корней уравнения 4-й степени, количество особых точек. Это уравнение здесь не приводим ввиду его громоздкости.
В табл.3 представлены значения параметров модели и начальные условия, которые принимались при изучении системы (2).
Таблица 3
Параметры и начальные условия модели 
| a | b | c | d | e | f | g | h |
| 2,5 | 0,2 | 0,5 | 1,5 | ||||
| k | m | X | Y | Z | X0 | y0 | z0 |
| 0,5 |
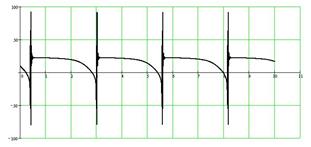
Практический интерес представляет решение системы, полученное при f = 8 (1/мин) и приведенное на рис.5. Здесь имеет место циклический характер работы системы. Временная зависимость переменных x и y показывает изменение числа автобусов и пассажиров на остановке, напоминающее известные функции из теории управления запасами, как и в модели (1). В течение некоторого времени число автобусов на остановке плавно уменьшается, число пассажиров остается до определенного момента почти постоянным, затем их количество заметно уменьшается и практически мгновенно (в масштабе времени одного цикла) осуществляется интенсивный переходный процесс, связанный с накоплением пассажиров и автобусов до исходного уровня. Эти пилообразные кривые представляют своего рода временные (контрастные, как и в модели грузового склада) структуры, показывающие согласованный характер работы всех элементов (остановок) макросистемы, т.е. самоорганизацию. Изучение подобных структур в реальных системах позволит сформулировать постановку задачи теории управления для создания требуемых типов временных структур в течение дня работы автобусного парка.
В модели реализуется каскад бифуркаций, приводящих к нерегулярному аттрактору. Параметры, приведенные в таблице, соответствуют этому решению, которое показано на рис.6. Таким образом, в системе уравнений (2) также имеется детерминированный хаос, возникающий в результате гомоклинического каскада бифуркаций [4].

| 
|
а б
Рис.5. Решение модели (2) при f = 8 (1/ мин):
а – временные зависимости; б – фазовый портрет


| 

|
а б
Рис.6. Хаотический аттрактор в модели пассажирской остановки:
а – временные зависимости; б – проекции фазового портрета