Структурные группы плоских рычажных механизмов

Условие существования структурных групп плоских рычажных механизмов описывается формулой

W = 3n - 2P₅ = 0.

Так как количество подвижных звеньев механизма n и количество кинематических пар P₅ – целые числа, то соответственно

,

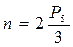откуда можно сделать вывод, что количество звеньев n в структурной группе кратно 2, или чётно.

А так как количество кинематических пар в структурной группе описывается формулой

,

то отсюда можно сделать вывод, что количество кинематических пар P₅ в структурной группе кратно 3.

Примеры структурных групп приведены на рис. 1.3.

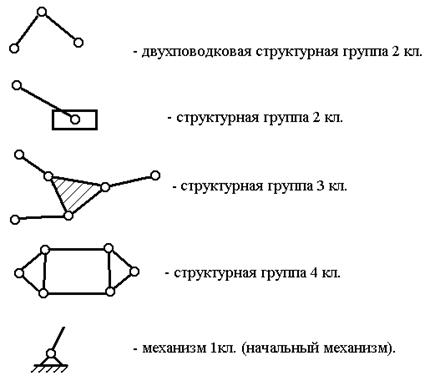
Рис.1.3. Примеры структурных групп.

При добавлении к механизму 1-го класса различных структурных групп можно получить механизм, состоящий из одной или нескольких структурных групп и механизма 1-го класса.

Механизмам, состоящим из одной или нескольких структурных групп, присваивается определённый класс. Класс механизма соответствует наивысшему классу входящих в него структурных групп. Примеры механизмов различных классов приведены на рис.1.4.

Рис. 1.4. Механизмы различных классов

Порядок структурной группы равен числу свободных кинематических пар, которыми она присоединяется к более простому механизму. Примеры структурных групп 1-го, 2-го и 3-го порядков приведены на рис.1.5. Здесь стрелками показаны свободные кинематические пары, которыми эти структурные группы могут подсоединяться к другим звеньям или структурным группам при синтезе механизмов.

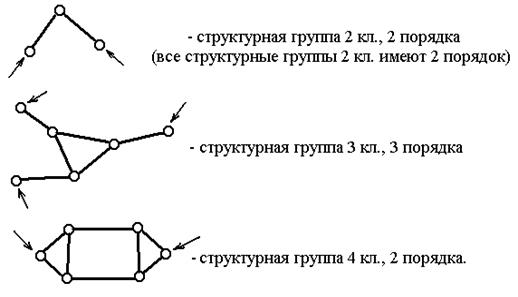
Рис.1.5. Порядок структурных групп

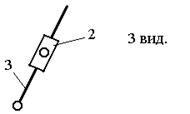
Очень широко распространены плоские рычажные механизмы, в состав которых входят структурные группы 2-го класса. Эти структурные группы подразделяют на 5 видов (модификаций). Их кинематические схемы приведены в таблице 1.1. Первый вид имеет два звена и три вращательные кинематические пары, во втором виде одна из крайних вращательных пар заменена поступательной, в третьем виде поступательной парой заменена средняя вращательная пара, в четвертом виде две крайние вращательные заменены двумя поступательными, а в пятом виде поступательными парами заменены крайняя и средняя вращательные пары. Каждый из видов этих структурных групп, будучи присоединен к начальному механизму, состоящему из стойки и кривошипа, образует определенный тип простейшего рычажного механизма: шарнирный четырехзвенник, кривошипно-ползунный, кулисный, тангенсный или синусный механизмы.

Таблица 1.1

Виды структурных групп 2-го класса

Кинематические схемы структурных групп 1…5 видов	Механизмы, содержащие соответствующие структурные группы

Для определения класса механизма его необходимо расчленить на структурные группы, начиная с конца механизма. За начало механизма принимают ведущее звено (начальный механизм).

От конца механизма отделяются поочерёдно простейшие структурные группы до тех пор, пока не останется лишь механизм 1-го класса (начальный механизм). Причем следует иметь в виду, что начальных механизмов может быть несколько.

Класс механизма определяется по наивысшему классу входящих в него структурных групп. Количество начальных механизмов равно величине W.

На рисунке 1.6 показан пример расчленения рычажного механизма на структурные группы. Предварительно вычисляют степень подвижности механизма W по формуле:

W = 3n - 2P₅ - P₄..

В данном случае W = 1, а это говорит о том, что в механизме должно быть одно ведущее звено и, соответственно, один начальный механизм. Затем отделяется структурная группа 2 класса 2 вида, состоящая из звеньев 4 и 5, а за ней – структурная группа 2 класса 1 вида со звеньями 2 и 3.

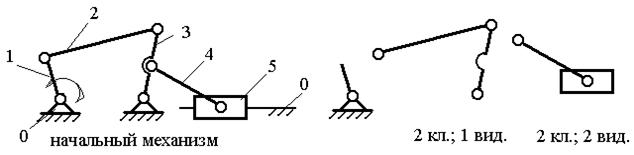Рис. 1.6. Расчленение механизма на структурные группы

Избыточные связи

В некоторых случаях при проектировании механизмов вводятся так называемые избыточные связи (дополнительные звенья) для повышения жёсткости конструкции, улучшения условий передачи сил и т.д. (рис. 1.7.)

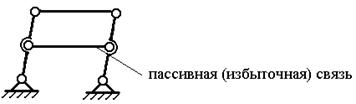
Рис. 1.7. Механизм с избыточной связью

В этом случае степень свободы вычисляется по формуле

W = 3n - 2P₅ – q,

где q – число пассивных связей.

Лишние степени свободы

Лишние степени свободы, которыми обладает механизм, используются, как правило, для упрощения кинематической схемы или повышения КПД механизма.

Например, между кулачком 1 и толкателем 2 кулачкового механизма устанавливается ролик 3, служащий для уменьшения трения (рис. 1.8).

Рис. 1.8. Кулачковый механизм с роликовым толкателем.

В этом случае степень подвижности механизма, вычисленная по формуле П.Л. Чебышева, будет равна 2:

W = 3n - 2P₅ - P4 = 3 ^. 3 – 2 ^. 3 - 1 = 2.

Здесь явно присутствует лишняя степень свободы, а именно вращение ролика под действием силы трения качения. Её следует учитывать при проведении структурного анализа данного механизма. Ведь очевидно, что механизм может функционировать и без ролика 3. Но при этом трение качения будет заменено трением скольжения между кулачком и толкателем (то есть кулачек и толкатель образуют высшую кинематическую пару).