Последовательность кинематического анализа
1. Сначала строятся несколько (чаще всего 12) совмёщенных планов механизма в произвольно выбранном масштабе длин.
2. Затем строится график пути (перемещения) исследуемой точки или звена. Для этого используют совмещённые планы механизма и последовательные положения на них исследуемой точки или звена.
3. Графическим дифференцированием графика перемещений строится график скорости исследуемой точки.
4. Графическим дифференцированием графика скоростей строится график ускорений.
Графическое дифференцирование можно производить методом хорд и методом касательных. Удобно использовать оба метода одновременно.
Пример
Дано: кривошипно-ползунный механизм, длины звеньев которого - кривошипа и шатуна - LOA и LAB соответственно; угловая скорость кривошипа w1 = const.
Выполнить: определить скорости и ускорения ползуна при различных положениях кривошипа.
Решение
Выбираем масштабы длин  [м/мм], где AO – длина отрезка в мм, изображающая кривошип длиной LAB на строящемся плане механизма; выбирается произвольно с учётом того, что совмещённые планы должны разместиться на отведённом месте чертежа, а сам масштаб был бы удобен для расчётов.
[м/мм], где AO – длина отрезка в мм, изображающая кривошип длиной LAB на строящемся плане механизма; выбирается произвольно с учётом того, что совмещённые планы должны разместиться на отведённом месте чертежа, а сам масштаб был бы удобен для расчётов.
Вычисляем  [мм]. При построении планов механизма используют метод засечек (рис.2.1).
[мм]. При построении планов механизма используют метод засечек (рис.2.1).
Для построения графиков скоростей и ускорений выбираются полюсные расстояния hu и ha, причем:
hu – полюсное расстояние при построении графика скоростей, которое выбирается произвольной длины; рекомендуется его величину выбирать в пределах hu » 30…40 мм;
ha – полюсное расстояние при построении графика ускорений; его рекомендуется принимать в пределах ha »30…40 мм.

Рис. 2.1. Совмещённые планы механизма, графики перемещений, скоростей и ускорений.
Вычисление масштабов времени, скорости и ускорения проводится по формулам, вывод которых приводится ниже.
Масштаб времени можно вычислить по формуле
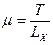 ,
,
где Т – период одного оборота кривошипа, сек,
LX – длина отрезка между точками 1 и 1 на графике (диаграмме) перемещений, м.
Так как период Т можно вычислить по формулам
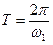 , с или
, с или  , с,
, с,
где n1 – частота вращения кривошипа, об/мин, то масштаб времени равен
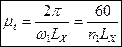 , с/мм.
, с/мм.
Масштаб скорости можно вывести из условия, что скорость исследуемой точки является производной по времени:
 .
.
Так как 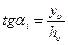 , то
, то 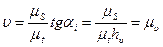 ,
,
отсюда  ,
,  .
.
Масштаб ускорения, вывод которого аналогичен предыдущему, вычисляется по формуле
 ,
,  .
.
Для определения величины скорости или ускорения в каком-либо положении точки В необходимо длину ординаты соответствующего графика умножить на масштаб mu или ma соответственно.
2.3 Графоаналитический метод кинематического анализа
Его называют также методом планов скоростей и ускорений.
Преимущества этого метода по сравнению с графическим следующие: он менее трудоёмок, так как позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма.
Недостатком метода является то, что требуется построить планы скоростей и ускорений для нескольких положений механизма (если необходимо определять скорость и ускорение при различных положениях механизма и, соответственно, его звеньев).
Задача о положениях решается так же, как и в графическом методе, то есть построением нескольких совмещённых планов механизма в выбранном масштабе длин.
Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений.
2.4. Планы скоростей и ускорений шарнирного четырёхзвенника
Как правило, при решении задач такого типа являются известными угловая скорость w1 ведущего звена 1 – кривошипа, а также длины звеньев и координаты неподвижных точек.
Последовательность решения задачи:
а) Строится план механизма (рис. 2.2) в выбранном масштабе длин mL:
 , м/мм,
, м/мм,
где LOA – длина кривошипа, м,
AO – длина отрезка, изображающего кривошип плане механизма, мм.
Для построения плана механизма остальные длины звеньев и координаты неподвижных точек переводятся масштабом длин mL в отрезки:
AB = LAB/mL, мм;
BC = LBC/mL, мм;
OC = LOC/mL, мм.
б) Составляются векторные уравнения линейных скоростей отдельных точек, принадлежащим звеньям механизма.
Векторное уравнение для звена 2 (шатуна):
V В = V А + V ВА,  (1)
(1)
где V А = V АО - скорость точки А, которая равна скорости точки А относительно точки О;
V ВА - вектор относительной скорости точки В относительно А; он имеет направление, перпендикулярное прямой АВ на плане механизма.
Векторное уравнение для звена 3 (коромысла):
V В = V С + V ВС. (2)
Так как точка С (ось вращения коромысла 3) неподвижна, то её скорость равна нулю (V С = 0), а вектор относительной скорости точки В относительно С (V ВС) имеет направление, перпендикулярное прямой ВС на плане механизма.
в) Строится план скоростей механизма. План скоростей – это не что иное, как графическое изображение на чертеже векторных уравнений (1) и (2) в каком-либо масштабе.
План скоростей механизма и его свойства
План скоростей желательно строить рядом с планом механизма (рис. 2.2.). Предварительно рассчитывается скорость точки А:
 , м/с
, м/с
Затем выбирается масштаб плана скоростей mu по соотношению:
 ,
,  ,
,
где uA – скорость точки А, м/с;
PVa – длина отрезка, изображающего на будущем плане скоростей скорость V A; выбирается произвольной длины в мм; при выборе желательно придерживаться следующих условий: во-первых, чтобы план механизма разместился на отведённом месте чертежа, и, во-вторых, чтобы численное значение масштаба mu было удобно для расчётов (другими словами – чтобы mu был круглым числом).
После этого можно приступать к построению плана скоростей механизма. Его желательно проводить в последовательности, соответствующей написанию векторных уравнений (1) и (2).
Сначала проводится из произвольно выбранной рядом с планом механизма точки Рu (полюса плана скоростей) вектор скорости V А, который перпендикулярен отрезку ОА на плане механизма и имеет длину PVa. Её мы выбрали при определении масштаба плана скоростей mu.
Затем через точку a проводится линия, перпендикулярная отрезку АВ плана механизма, а через полюс PV – линия, перпендикулярная отрезку ВС. Пересечение этих линий даёт точку b, и в соответствие с векторными уравнениями (1) и (2) наносятся направления (стрелки) векторов V В и V ВА.
Определим скорость точки К, принадлежащей шатуну. Для неё можно записать следующие векторные уравнения скоростей:
V К = V А + V КА;
V К = V В + V КВ.
Здесь вектор скорости V КА перпендикулярен прямой АК на плане механизма, а вектор V КВ – прямой КВ. Построением этих векторных уравнений получаем точку k на плане скоростей. Величину скорости точки К можно вычислить по формуле
VК = (РVk) . mV,
где РVk – длина соответствующего вектора на плане скоростей.
Можно заметить, что треугольники на плане скоростей и плане механизма подобны:
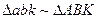 ,
,
так как стороны их взаимно перпендикулярны. Это свойство можно использовать для определения скорости любой другой точки, принадлежащей какому либо звену механизма. Отсюда следует теорема подобия:
Отрезки относительных скоростей на плане скоростей образуют фигуру, подобную фигуре соответствующего звена на плане механизма. Стороны фигур взаимно перпендикулярны.
Угловые скорости шатуна 2 и коромысла 3 рассчитываются по формулам
 , [c-1],
, [c-1],
 , [c-1].
, [c-1].
Направление угловых скоростей определяются по направлениям векторов V ВА и V ВС.
План ускорений механизма и его свойства
Последовательность построения плана ускорений рычажного механизма аналогична построению плана скоростей. Рассмотрим её на примере механизма шарнирного четырехзвенника (рис.2.2). Причём примем, что угловая скорость кривошипа постоянна (w1 = const, что является наиболее рациональным и распространённым движением в реальных механизмах).
Векторное уравнение ускорений для звена 1 (кривошипа)
а А= а АО = а nАО+ а tАО ,
где нормальная составляющая ускорения точки A относительно O рассчитывается по формуле
 ;
;
причем вектор а nАО параллелен отрезку АО на плане механизма. Тангенциальная составляющая ускорения а tАО рассчитывается по формуле
 .
.
В нашем случае угловое ускорение кривошипа e1 = 0.
Векторное уравнение ускорений для звена 2 (шатуна)
а В= а А + а nВА+ а tВА,
где нормальная составляющая ускорения точки А относительно точки О рассчитывается по формуле
 ,
,
причем вектор а nВА параллелен отрезку АВ, а тангенциальная составляющая а tВА перпендикулярна АВ.
Векторное уравнение ускорений для звена 3 (коромысла)
а В= а С + а nВС+ а tВС,
где ускорение точки С а С = 0, нормальная составляющая ускорения точки В относительно точки С рассчитывается по формуле
 ,
,
вектор а nВС направлен параллельно прямой ВС плана механизма от В к С, а вектор а tВС направлен перпендикулярно ВС.
Выбираем масштаб плана ускорений: 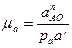 ,
,  .
.
Тогда ускорение а nВА будет изображаться на плане ускорений вектором, имеющим длину  , [мм], а ускорение а nВС - вектором длиной
, [мм], а ускорение а nВС - вектором длиной 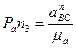 , [мм].
, [мм].
Затем строится план ускорений (рис.2.2) с использованием составленных векторных уравнений ускорений.
Используя план ускорений (рис.2.2), можно вычислить ускорения:
 ,
,  mu.
mu.
Можно записать так: 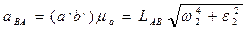 , где w2 и e2 – угловые скорость и ускорение шатуна. Из этого уравнения следует:
, где w2 и e2 – угловые скорость и ускорение шатуна. Из этого уравнения следует:
 .
.
В этом уравнении w2 и e2 не зависят от выбора (расположения) полюса Ра плана ускорений, отношение  для данного плана ускорений. Поэтому для любой точки (например К, принадлежащей шатуну) можно записать следующие пропорции:
для данного плана ускорений. Поэтому для любой точки (например К, принадлежащей шатуну) можно записать следующие пропорции:
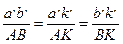 .
.
Отсюда формулируется теорема подобия:
Отрезки полных относительных ускорений на плане ускорений образуют фигуру, подобную соответствующей фигуре звена на плане механизма.
 .
.
Угловые ускорения звеньев:
шатуна:  , [c-1], направление e 2 определяется по а tВА;
, [c-1], направление e 2 определяется по а tВА;
коромысла:  , [c-1]; направление e 3 определяется по а tВс.
, [c-1]; направление e 3 определяется по а tВс.
Так как w 2 и e 2 направлены в противоположные стороны, вращение шатуна является замедленным.
 Рис. 2.2. План механизма, планы скоростей и ускорений.
Рис. 2.2. План механизма, планы скоростей и ускорений.
Использование плана скоростей и плана ускорений
для определения радиуса кривизны траектории движения точки
Радиус кривизны траектории движения точки (например, точки К) можно вычислить по следующей формуле
 ,
,
где а nК - нормальная составляющая ускорения точки К.
Для определения величины (и направления) а nК следует на плане ускорений вектор полного ускорения а К разложить на нормальную и тангенциальную составляющие, причём а nК перпендикулярна вектору скорости V R, а tК параллельна последнему.
Сначала через полюс плана ускорений Ра проводится прямая, параллельная вектору скорости точки К, а через точку k` - перпендикуляр к этой прямой.
Использование плана скоростей и плана ускорений
для определения мгновенного центра скоростей (МЦС) и мгновенного центра ускорений (МЦУ) звена
Для этого используют теорему подобия, а именно на плане механизма строят фигуры, подобные фигурам (треугольникам) на планах скоростей и ускорений (рис.2.3):

Рис. 2.3. Определение положений мгновенных центров скоростей и PV2 и ускорений Ра2 шатуна.
Из теоретической механики известно, что при плоскопараллельном движении звена механизма это движение в каждый момент времени может быть представлено как вращение вокруг некоторой точки, которую называют мгновенным центром вращения или мгновенным центром скоростей (МЦС). Если данная точка относится к станине (стойке) механизма, то есть является неподвижной, то соответствующий МЦС называют мгновенным центром скоростей в абсолютном движении рассматриваемого звена. Таким образом, если мы представим, что точка PV2 принадлежит шатуну (рис.2.3), то её скорость будет равна нулю.
Если же рассматривается движение звена относительно любого подвижного звена механизма, то соответствующий МЦС называют мгновенным центром скоростей в относительном движении рассматриваемых звеньев.
Аналогично мгновенному центру скоростей звена для общего случая его движения может быть найдена условная точка, принадлежащая звену, абсолютное ускорение которой в данный момент времени равно нулю. Эта точка называется мгновенным центром ускорений (МЦУ) звена.
Очевидно, что если звено механизма совершает сложное плоскопараллельное движение, то меняются и положения МЦС и МЦУ.
Планы скоростей и ускорений кривошипно-ползунного механизма
Последовательность построения планов скоростей и ускорений кривошипно-ползунного механизма аналогична той, которая приведена в предыдущем случае. Поэтому в дальнейшем некоторые подробности (расчёты масштабов, длин mе, масштабов планов скоростей mv и ускорений mа и т.д.) будет пропущены.

Рис. 2.4. Построение планов скоростей и ускорений
кривошипно-ползунного механизма.
План скоростей кривошипно-ползунного механизма начинают строить после построения плана механизма в заданном положении, в выбранном масштабе длин mL, составления векторного уравнения скоростей и выбора масштаба плана скоростей mv.
Векторное уравнение скоростей:
V В = V А + V ВА,
где VА = w1 LOA – скорость точки А, м/с; вектор этой скорости направлен
перпендикулярно прямой ОА (кривошипу 1) на плане механизма;
V ВА – вектор скорости точки В относительно А; он имеет направление, перпендикулярное прямой АВ на плане механизма;
V В – вектор полной (абсолютной), скорости ползуна 3; этот вектор должен быть параллельным направлению движения ползуна.
Построения плана скоростей проводится в следующей последовательности. Сначала из полюса плана Рv (рис.2.4) проводится вектор скорости точки А относительно О - V А. На плане скоростей это векторный отрезок Рva. Затем через точку а проводится перпендикуляр к прямой АВ плана механизма, и через полюс Рv – прямая, параллельная движению ползуна 3. На пересечении этих двух прямых получается точка В. Обозначают направление векторов (“стрелки”) скоростей V В и V ВА.
Если, например, необходимо определить скорость точки S2, принадлежащей шатуну 2 и расположенной на середине отрезка АВ, то, используя теорему подобия, на отрезке ab плана скоростей находится его середина (точка S2), которая, будучи соединенная с полюсом Рv, даст вектор V S2, изображающий абсолютную (полную) скорость точки S2.
Рассчитываются величины линейных скоростей и угловая скорость шатуна
 , м/с;
, м/с;
 , м/с;
, м/с;
 , м/с;
, м/с;
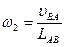 , с-1.
, с-1.
Направление вектора угловой скорости шатуна w 2 определяется следующим образом. Нужно вектор скорости V ВА условно перенести в точку В плана механизма и посмотреть, куда он будет вращать шатун относительно точки А. В ту сторону и направлена угловая скорость w 2 шатуна.
План ускорений кривошипно-ползунного механизма строится после того, как будет составлено векторное уравнение ускорений шатуна, учитывая, что он совершает сложное движение:
а В= а А + а nВА+ а tВА.
Здесь а А – ускорение точки А; его величину и направление можно определить, используя векторное уравнение ускорения точки А относительно оси О вращения кривошипа:
а А= а О + а АО,
причём ускорение точки А относительно О можно разложить на две составляющих – нормальное ускорение а nАО и тангенциальное а tАО, т.е.
а АО = а nАО+ а tАО.
Так как точка О неподвижна и ускорение её равно нулю (а О = 0 и а tАО = 0 при условии, если угловая скорость вращения кривошипа постоянна: w1 = const, и, значит, угловое ускорение его e1 = 0), то векторное уравнение ускорения точки А запишется в виде:
а А= а nАО .
Величина нормальной составляющей ускорения (нормальное ускорение) рассчитывается по формуле
 .
.
Вектор его направлен по радиусу вращения кривошипа от точки А к точке О.
Затем вычисляется нормальное ускорение точки В относительно А по формуле

Вектор его направлен от В к А.
После выбора масштаба плана ускорений по формуле 
величина нормального ускорения a nBA переводится этим масштабом в векторный отрезок длиной
 , мм.
, мм.
Затем строится план ускорений в следующей последовательности (рис. 2.4). Из произвольно выбранного полюса Ра параллельно прямой АВ плана механизма проводится вектор ускорения a nAО, длина которого 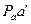 была выбрана произвольно при расчёте масштаба mа. Из конца этого вектора (точки
была выбрана произвольно при расчёте масштаба mа. Из конца этого вектора (точки  ) проводится вектор ускорения a nBA длиной
) проводится вектор ускорения a nBA длиной  , который должен быть параллелен прямой АВ плана механизма и направлен от точки В к А. Перпендикулярно ему через точку n2 проводится прямая до пересечения с прямой, проведённой через полюс Ра параллельно линии движения ползуна 3. Полученная точка их пересечения
, который должен быть параллелен прямой АВ плана механизма и направлен от точки В к А. Перпендикулярно ему через точку n2 проводится прямая до пересечения с прямой, проведённой через полюс Ра параллельно линии движения ползуна 3. Полученная точка их пересечения  определяет длины векторов ускорений a BA и a B.
определяет длины векторов ускорений a BA и a B.
Для нахождения величины ускорения точки S2, принадлежащей шатуну, можно применить теорему подобия. При этом необходимо на векторе, изображающем на плане ускорений относительное ускорение a BA, найти соответствующую точку S2’, делящую отрезок  в той же пропорции, что и точка S2 делит отрезок АВ на плане механизма.
в той же пропорции, что и точка S2 делит отрезок АВ на плане механизма.
Угловое ускорение шатуна вычисляется по формуле:
 , с-1.
, с-1.
где  – длина вектора на плане ускорений, изображающего тангенциальное ускорение а tВА.
– длина вектора на плане ускорений, изображающего тангенциальное ускорение а tВА.
Направление вектора углового ускорения шатуна e 2 определяется следующим образом. Нужно вектор тангенциального ускорения а tВА условно перенести в точку В плана механизма и посмотреть, куда он будет вращать шатун относительно точки А. В ту сторону и направлено ускорение e 2 шатуна.
Планы скоростей и ускорений кулисного механизма

Рис. 2.5. Построение планов скоростей и ускорений кулисного механизма
Чтобы построить план скоростей, необходимо составить векторное уравнение скоростей. При этом следует иметь в виду, что точка А1, принадлежащая кривошипу 1, и точка А2, принадлежащая ползуну 2 и совпадающая на плане механизма с точкой А1, вращаются вокруг оси О с одинаковыми линейными и угловыми скоростями:
V А1 = V А2 и  .
.
Если задана величина w 1, то величину линейной скорости рассчитывают по формуле:
VА1 = VА2 = w1 LОА, м/с.
Векторы скоростей V А1 и V А2 направлены перпендикулярно радиусу ОА1. Скорость точки А3, принадлежащей кулисе 3, можно найти по следующему векторному уравнению скоростей:
V А3 = V А2 + V А3А2,
где V А3А2 – вектор скорости точки А3 кулисы относительно точки А2 ползуна; он перпендикулярен прямой А1В плана механизма.
После выбора масштаба плана скоростей mv (см. предыдущие примеры механизмов) строят план скоростей в следующей последовательности.
Из полюса Рv (рис.2.5) перпендикулярно отрезку ОА плана механизма, проводится вектор скорости V А1, совпадающий с вектором скорости V А2. На рис. 2.5 это вектор 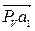 . Через точку а 1 проводится прямая, параллельная прямой А1В, а через полюс Рv – прямая, перпендикулярная А1В. На их пересечении получают точку а 3 и наносят направление векторов (“стрелки”), руководствуясь векторным уравнением скоростей.
. Через точку а 1 проводится прямая, параллельная прямой А1В, а через полюс Рv – прямая, перпендикулярная А1В. На их пересечении получают точку а 3 и наносят направление векторов (“стрелки”), руководствуясь векторным уравнением скоростей.
Вычисляют величины скоростей:
 , м/с;
, м/с;
 , м/с.
, м/с.
где Рva3 и а1а3 – длины векторов, измеренные на плане скоростей.
Угловая скорость коромысла 3 вычисляется по формуле
 ,с-1.
,с-1.
Для построения плана ускорений составляются следующие векторные уравнения:
а А3= а А2 + а корА3А2+ а отнА3А2 ,
а А3= а В + а nА3В+ а tА3В,
где а А2 – ускорение ползуна,
а корА3А2 – Кориолисово ускорение точки А3 относительно А2 (возникает тогда, когда есть относительное движение двух точек с одновременным вращением их вокруг какой-либо оси; в данном случае точка А3 движется относительно А2, и вместе они вращаются вокруг неподвижной точки В); направление вектора а корА3А2 определяется так – необходимо условно повернуть вектор скорости V А3А2 по направлению вращения кулисы 3, это и будет направление Кориолисова ускорения;
а отнА3А2 - относительное ускорение точки А3 относительно А2; его вектор параллелен А3В;
а В - ускорение точки В; а В = 0, так как точка В неподвижна;
а nА3В - нормальное ускорение точки А3 относительно В; направление вектора – от А3 к точке В;
а tА3В - тангенциальное ускорение точки А3 относительно В; вектор направлен перпендикулярно А3В.
Вычисление величины Кориолисова и нормальных ускорений можно произвести по следующим формулам:
аА2 = аnА1О = w21 LОА, м/с2;
акорА3А2 = 2w3 VА3А2, м/с2;
аnА3В = w23 LА3В, м/с2.
Выбирается масштаб плана ускорений с использованием формулы
 ,
, 
где Раа2 – длина вектора, изображающего ускорение а А2 на плане ускорений; она выбирается произвольной длины с таким расчётом, чтобы, во-первых, будущий план ускорений разместился на отведённом месте чертежа, и, во-вторых, чтобы масштаб был удобен для использования в дальнейших расчётах (был “круглым числом”).
Остальные известные величины ускорений переводятся масштабом в векторные отрезки соответствующих длин
 , мм;
, мм;
 , мм.
, мм.
Затем строится план ускорений в следующей последовательности.
Из произвольно выбранного полюса – точки Ра – проводится вектор ускорения а nА1О с длиной Раа2’. Из точки а 2’перпендикулярно А2В проводится вектор ускорения а корА3А2 с длиной  . Через точку k проводится прямая, перпендикулярная к этому вектору. Таким образом, будет выполнено графическое изображение первого векторного уравнения ускорений из двух ранее составленных.
. Через точку k проводится прямая, перпендикулярная к этому вектору. Таким образом, будет выполнено графическое изображение первого векторного уравнения ускорений из двух ранее составленных.
Затем приступают к построению второго векторного уравнения. Из полюса Ра параллельно прямой А3В проводится вектор ускорения а nА3В длиной Раn2, и через точку n2 – перпендикулярная ему прямая до пересечения с прямой, проведённой ранее через точку k. На пересечении этих прямых получается точка а 3’. Вектор, соединяющий точки Ра и а 3’, есть полное ускорение а А3 точки А3.
Затем вычисляется угловое ускорение кулисы по формуле
 , с-2,
, с-2,
где n 2 a 3` – длина вектора, изображающего на плане ускорений тангенциальное ускорение точки А3.
Направление углового ускорения определяется, как и в предыдущем примере (для кривошипно-ползунного механизма), то есть по направлению условного вращения кулисы 3 вектором ускорения а tА3В. При этом нужно условно перенести этот вектор в точку А3 плана механизма и посмотреть, в каком направлении он будет «вращать» кулису.