Истина — это то, что выдерживает проверку опытом.
Альберт Эйнштейн
В данной теме речь пойдёт о давлении в жидкости и газе, а также о расчёте давления жидкости на дно и стенки сосуда.
Ранее было установлено, что в отличие от твердых тел, жидкости и газы передают производимое на них давление не направленно, а во все стороны.
Благодаря тому, что молекулы в жидкости обладают достаточной подвижностью, то жидкость может принимать форму того сосуда, в который она налита. И если на жидкость действует внешняя сила давления, то, согласно закону Паскаля, жидкость передает созданное этой силой давление во все точки без изменений.
Однако напомним, что закон Паскаля применим только к жидкостям и газам, а в твердых телах подвижность молекул ограничена, и они не подчиняются этому закону.
Рассмотрим опыт с картезианским водолазом (Картезианский водолаз — механическая игрушка, основанная на изменении плавучести при сжатии. Первое описание водолаза было дано итальянским учёным Рафаэлло Маджотти в 1648 году). Пусть водолаз находится в высокой стеклянной трубке, заполненной водой. Сверху эта трубка затянута резиновой пленкой. Нажмем пальцем на пленку — водолаз тонет. Отпустим палец — водолаз начинает всплывать. А теперь нажмем еще раз и подождем, чтобы водолаз опустится на самое дно нашей трубочки. Отпустим палец — а водолаз не всплывает, он остался лежать на дне. Это странно, ведь сверху на пленку ничего не давит. Что же тогда удерживает водолаза внизу?
Чтобы водолаз не всплывал, нужно, чтобы воздух внутри него был сжат внешним давлением. Раньше это давление создавалось пальцем. А чем создается это давление теперь?
Над водолазом находится высокий столб воды. Не трудно догадаться, что на воду в трубке, как и на все тела на Земле, будет действовать сила тяжести. Поэтому каждый слой жидкости, налитой в сосуд, своим весом создает давление на другие слои, которое, согласно закону Паскаля, передается по всем направлениям.

Таким образом, жидкость давит на стенки и дно сосуда, а, следовательно, и на нашего водолаза. В том, что жидкость действительно создает давление, можно убедиться, используя эластичный полиэтиленовый пакет или трубку, нижний конец которой закрыт эластичной пленкой. Если постепенно наливать воду в сосуд, то можно обнаружить, что прогиб пленки увеличивается с увеличением количества воды.
Причиной увеличения прогиба является рост давления воды на пленку. Притягиваясь к Земле, жидкость давит своим весом на пленку подобно тому, как давит на стол стопка книг.
Проведем еще один опыт. Возьмем трубку с эластичным дном, в которую уже налита вода, и будем медленно погружать ее в другой, более широкий сосуд с водой. Можно заметить, что по мере опускания трубки ее эластичное дно начнет постепенно выпрямляться. И в тот момент, когда уровни жидкостей в обоих сосудах совпадут, эластичное дно в трубке полностью выпрямится. На основании проделанного опыта мы можем заключить, что силы, которые действуют на эластичную пленку сверху и снизу одинаковы, т.е. равны.

Таким образом, жидкость, благодаря своему притяжению к Земле, способна оказывать давление на дно сосуда. Но только ли на дно? Ведь в любом сосуде, помимо дна, есть еще и боковые стенки. Проведём эксперимент.
Если взять стеклянную трубку, но уже с боковым отверстием, закрытым эластичной пленкой, и также будем наливать в нее воду, то можно увидеть, что боковая мембрана также начала растягиваться.

Если погрузить эту трубку в другой сосуд с водой, то пленка снова выпрямится, как только уровни воды в трубке и сосуде сравняются. Следовательно, вновь силы, действующие на эластичную пленку, одинаковы со всех сторон.

Таким образом, на основании всех проделанных опытов, можно заключить, что внутри жидкости существует давление, которое на одном и том же уровне одинаково по всем направлениям. Однако с глубиной это давление увеличивается.
Давление неподвижной жидкости, обусловленное ее весом, называют гидростатическим давлением (от латинских слов «гидрос » — вода, и «статиос » — неподвижный).
Важно отметить, что не только жидкости, но и газы создают данный вид давления, так как они тоже имеют вес. Но стоит помнить, что вес газа, находящегося в сосуде, очень мал, из-за его очень маленькой плотности. Поэтому, во многих случаях его весовое давление не учитывается.
Как можно рассчитать гидростатическое давление? Для этого рассмотрим сосуд, который имеет форму прямоугольного параллелепипеда.
Давление столба жидкости высотой h на дно сосуда с вертикальными стенками и площадью дна S будет определятся по уже известной нам формуле

Силой давления является вес жидкости. А если жидкость неподвижна, то ее вес будет равен силе тяжести.
F д = P = mg
В записанной нами формуле, неизвестной величиной является масса, которую можно определить, как произведение плотности жидкости и ее объема.
m = rV
Считаем, что плотность налитой нами жидкости известна. Объем жидкости можно рассчитать, зная высоту столба жидкости, налитой в сосуд и площадь его дна. Тогда выражение для массы запишется в виде:
m = rSh
Если подставить данное выражение для массы жидкости в формулу давления, то получим формулу, для расчета гидростатического давления

Из формулы видно, что давление жидкости на дно сосуда зависит только от ее плотности и высоты столба жидкости. Следовательно, по этой формуле можно рассчитывать гидростатическое давление жидкости, налитой в сосуд любой формы.

Чтобы проверить это, к нашему прибору с эластичным дном присоединим измерительную систему. При замене цилиндрического сосуда на сосуды разной конической формы, но с одинаковой площадью дна, в которых высоты столбов жидкости будут равные, прибор будет показывать равные силы давления, а значит, и равные давления жидкости на дно всех сосудов, хотя масса жидкости в сосудах разная. Это явление известно в физике под названием гидростатический парадокс, который можно объяснить законом Паскаля.
Рассмотрим сосуд изображённый на рисунке.

На площадку MN дна сосуда действует сила, равная весу столба жидкости KLMN, которая производит гидростатическое давление.

По закону Паскаля такое давление передается и на площадку AM, и на площадку NB.

Значит сила, действующая на все дно, будет равна весу вертикального столба жидкости ABCD.

Формула для расчета гидростатического давления позволяет найти давление не только на дно сосуда, но и на его боковые стенки. Проверим это на опыте. Возьмем пластиковую бутылку с проколотыми в стенке отверстиями и нальем в нее подкрашенную воду.

Наблюдение за вытекающими струями показывают, что гидростатическое давление действует и на стенку бутылки, а его величина возрастает с увеличением высоты столба воды. Поэтому самая нижняя струйка воды падает дальше, чем самая верхняя.
Как объяснить происходящее? Для этого мысленно разделим жидкость на слои.

На каждый нижний слой жидкости действует вес верхних слоев. Сила тяжести, действующая на первый слой, прижимает его ко второму, который, в свою очередь, передает производимое на него давление по всем направлениям. На третий слой уже действует вес первого и второго слоя. Значит, давление, оказываемое на третий слой, будет больше, чем давление во втором слое. Таким образом, наибольшим давление будет на дно сосуда и, соответственно, стенку у дна.
Примерно так же в 1648 году рассуждал и Блез Паскаль. Он решил, что если взять тонкую и длинную трубку, то можно совсем небольшим количеством воды создать огромное давление. Для того, чтобы в этом удостоверится, он поместил такую трубку в закрытую со всех сторон бочку с водой. Поднявшись на балкон второго этажа дома, он вылил в узкую трубку несколько кружек воды, и, на удивление собравшихся зевак, давление на стенки бочки так возросло, что клепки бочки разошлись, и вода из бочки стала выливаться.
Упражнения.
Задача 1. Определите дополнительное давление, действующее на ныряльщика на глубине 200 дециметров.

Задача 2. Резиновая камера заполнена водой и соединена со стеклянной трубкой так, как показано на рисунке. На камеру положена доска массой 1 кг и гиря массой 5 кг. Определите площадь доски, если высота столба воды в трубке составляет 1 м.

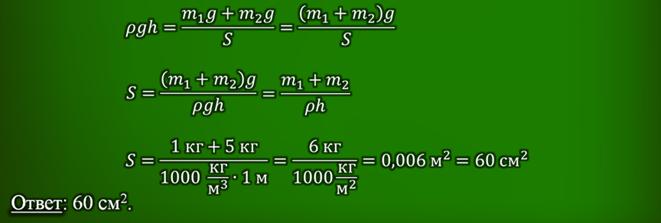
Наличие гидростатического давления является главным препятствием для проникновения человека в глубины Мирового океана. Ведь уже на глубине 2,5–3 м нетренированный ныряльщик испытывает сильнейшую боль в ушах, вызванную давлением воды на барабанные перепонки. Даже корпуса подводных лодок, изготовленные из самых прочных сплавов металла, на глубине несколько сот метров находятся на грани превышения допустимой прочности. Почему же некоторые виды рыб комфортно себя чувствуют на огромных глубинах (даже на дне Марианской впадины)?
Всё дело в том, что вода давит на рыб не только извне, но и изнутри, что приводит к компенсации сил давления.
Основные выводы:
– Жидкость создает давление за счет своего веса, причем не только на дно сосуда, в котором она находится, но и на его стенки.
– Давление неподвижной жидкости, обусловленное ее весом, называют гидростатическим давлением.
– Давление жидкости на дно сосуда зависит от плотности жидкости и высоты ее столба.
– Гидростатическое давление на боковую стенку сосуда на данной глубине такое же, как и на дно, если бы дно находилось на этой глубине.