В математике существуют различные численные методы вычисления определенных интегралов. Использование того или иного метода зависит от свойств подынтегральной функции на интервале интегрирования. В системе ML для вычисления определенных интегралов также существуют функции, реализующие различные методы. Это: trapz ( x, y) – метод трапеций, quad() – метод Симпсона, quadl() – метод квадратур Лобатто, quadgk() – метод Гаусса-Кронрода и др. (quadv()dblquad()) quad2 d() – вычисление двойного интеграла triplequad() - вычисление тройного интеграла.Методы отличаются точностью вычислений. Наиболее используемая функция - quadl()
Самым простым численным методом нахождения определенных интегралов является метод трапеций, который реализован функцией trapz (x, y),где x и y – векторы, задающие значения аргумента и функции в пределах интегрирования. Для ее использования не требуется оформление подынтегральной функции в качестве файла-функции.
Вычислим интеграл 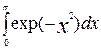 :
:
>> x=0:pi/100:pi;
y=exp(-x.^2);
z=trapz(x,y)
z =
0.886219032458507
.Все остальные функции имеют одинаковый набор параметров:
[i, n]=quadl (fun, a, b, tol, trace),
где
fun – имя файла-функции или символьное выражение, определяющее подынтегральную функцию (оно должно быть заключено в апострофы).
a, b – пределы интегрирования.
tol – погрешность вычислений.
trace– признак, если его значение равно единице, то при выполнении функции выдается последовательность из 4-х столбцов с промежуточными результатами (количество вычислений, левый конец промежутка, его длина, значение интеграла на этом промежутке), если нулю, то не выдается.
Последние два параметра являются необязательными.
Выходные значения:
i – значение интеграла;
n – количество значений функции, которое потребовалось вычислить для нахождения значения интеграла.
|
|
При использовании этих численных методов задаётся требуемая точность вычислений, а шаг подбирается автоматически (в отличие от функции trapz). По умолчанию точность равна 10-6.
Как мы уже знаем, функция может быть задана различными способами.
Например,
[i,n]=quadl(f, 0, pi, 1e-8, 0)
i =
0.886219059172834
n =
Если функция задана одним оператором, то удобнее использовать вариант с указателем на функцию (анонимная функция). Например, будем использовать функцию exp(-x^2)
Такую функцию можно указать прямо в команде вычисления интеграла:
[i, n] = quadl (@ (x) (exp(-x.^2)), 0, pi, 1e-8,0)
i =
0.886219059172834
n =
Или описать ее отдельной командой f = @ (x) (exp(-x.^2)), а затем использовать это имя:
>> f = @ (x) (exp(-x.^2));
>> [i, n]= quadl (f, 0, pi, 1e-8, 1)
18 0.0000000000 1.57079633e+000 0.8861600099
23 0.0000000000 1.44123248e-001 0.2804585210
28 0.2882464966 2.90034179e-001 0.4112828181
33 0.2882464966 2.66111317e-002 0.0481900338
38 0.3414687600 5.35523437e-002 0.0915703542
43 0.4485734474 6.48536139e-002 0.0995847932
48 0.5782806752 6.48536139e-002 0.0857482019
53 0.7079879030 5.35523437e-002 0.0599802482
58 0.8150925903 2.66111317e-002 0.0262091868
63 0.8683148537 3.51240737e-001 0.1711591410
68 0.8683148537 3.22269380e-002 0.0286510329
73 0.9327687298 6.48536139e-002 0.0480102371
78 1.0624759576 7.85398163e-002 0.0428677948
83 1.2195555902 7.85398163e-002 0.0292697717
88 1.3766352229 6.48536139e-002 0.0163103789
93 1.5063424507 3.22269380e-002 0.0060499256
98 1.5707963268 3.51240737e-001 0.0221700092
103 1.5707963268 3.22269380e-002 0.0049416447
108 1.6352502029 6.48536139e-002 0.0072543988
113 1.7649574307 7.85398163e-002 0.0053128603
118 1.9220370633 7.85398163e-002 0.0029117921
123 2.0791166960 6.48536139e-002 0.0013232772
128 2.2088239238 3.22269380e-002 0.0004260361
133 2.2732777999 2.90034179e-001 0.0011080957
138 2.8533461570 1.44123248e-001 0.0000404741
i =
0.8862190591 72834
n =
Такое же значение интеграла получим, если не укажем два необязательных параметра, но количество значений другое (т.к. другая точность вычислений):
|
|
[i, n]=quadl(f, 0, pi)
i =
0.8862190591 65851
n =
Для достижения разной точности понадобилось различное количество вычислений. Можно при вызове функции не указывать выходной параметр n. В этом случае не выводится количество значений функции, которое потребовалось, чтобы вычислить для нахождения значения интеграла.
[i, n]= quad (f, 0, pi, 1e-8, 0)
i =
0.886219059 339376
n =
n=quadgk (f, 0, pi)
i =
0.8862190591 72853
Решение уравнений
Часто приходится решать уравнения вида f(x)=0 на интервале a<x<b, где функция f(x) определена и непрерывна на заданном интервале.
Если функция представляет собой многочлен, то уравнение называется алгебраическим, если же в функцию входят тригонометрические, показательные, логарифмические функции, то оно называется трансцендентным.
Всякое x, обращающее функцию в 0 называется корнем уравнения, а способ нахождения этого x – решением f(x)=0.
Найти корни уравнения аналитически удается лишь в частных случаях, поэтому разработаны приближенные методы.
Для решения уравнений вида f(x)=0 (нахождения нулей функции f(x)) предназначена функция fzero,которая находит приближенное значение корня уравнения по заданному начальному приближению. Функция fzero находит значение аргумента, при котором функция обращается в ноль:
fzero(fun, x0),
где
fun – может быть указатель на функцию, или имя файл-функции ( m-файла ), заключенное в апострофы, или символьное выражение, определяющее функциональную зависимость (формулу), заключенное в апострофы. Для последнего искомая переменная должна обязательно называться x.
х0 – начальное значение х, от которого начнётся процесс поиска решения;
|
|
Если не задано начальное приближение, то сначала рекомендуется построить график этой функции на определенном отрезке. Затем, если корней несколько, то, задавая различные начальные значения, можно найти различные корни.
Вместо начального приближения вторым параметром можно задать отрезок, на котором лежит корень.
fzero(fun, [<нижн.гр. отр.> <верхн. гр. отр.>]),
Например, решим уравнение sin(x)-x2*cosx=0 на отрезке [-5 5].
Сначала построим график этой функции
>>fplot('sin(x)-x.^2.*cos(x)', [-5 5])
>>grid on

Из графика видно, что функция на этом отрезке имеет 4 корня: явно, при x=0, а остальные корни надо уточнять при различных начальных значениях. Получим различные корни:
Зададим анонимную функцию:
>> f=@ (x)(sin(x)-x.^2.*cos(x));
Найдем 1-й корень вблизи x=-5
>> x1=fzero(f,-5)
x1 =
-4.7566
Найдем 2-й корень вблизи x=-2
>> x2=fzero(f,-2)
x2 =
-1.8539
Найдем 3-й корень вблизи x=5
>> x3=fzero(f,5)
x3 =
4.6665
Для получения более точных значений можно установить формат long. По умолчанию корни находятся с точностью eps (встроенная переменная, равная 2.2204e-016).
Функция fzero() вычисляет только корни, в которых функция меняет знак, а не касается оси абсцисс.
В функции fzero первым параметром может быть встроенная функция, например:
>> fzero('sin',[2 4])
ans =
3.1416
При работе с этой функцией можно не только найти корень, но и получить значение функции в точке корня уравнения (проверка).
>> [x, res]=fzero(f, [2 5])
x =
4.6665
res =
-8.5487e-015
Значение корня находится приближенно, поэтому и значение функции отлично от 0.
При необходимости можно самостоятельно написать свои функции для решения уравнений, а затем использовать их как встроенные.