Исследование переходных процессов асинхронного двигателя

Лабораторная работа N 1.

 

1. Цель работы

1.1. Изучение математической модели асинхронного двигателя и реализация её в Simulink MATLAB.

1.2. Исследование с помощью математической модели переходных процессов асинхронного двигателя.

 

2. Программа и указания к выполнению работы

2.1 Описание математической модели

Моделирование различных режимов работы асинхронного двигателя удобно производить на базе математической модели в осях α, β, неподвижных в пространстве и сдвинутых на угол π/2. В рассматриваемой модели приняты следующие упрощающие допущения:

- магнитная цепь машины считается ненасыщенной;

- потерями в стали пренебрегается;

- асинхронный двигатель симметричен;

- напряжение питания симметрично и изменяется синусоидально;

- частота питающей сети постоянна.

Уравнения электрического равновесия обмоток статора и ротора по оси α имеют вид:

(1)

и по оси β:

(2)

В системах уравнений (1) şi (2)обозначено:

U_sα, U_sβ – составляющие напряжения питания статорной обмотки по осям α и β;

Y_sα, Y_rα, Y_sβ, Y_rβ – потокосцепления статорной и роторной обмотки по осям α и β;

i_sα, i_rα, i_sβ, i_rβ – токи статорной и роторной обмотки по осям α и β;

r_s şi r_r – активные сопротивления статорной и роторной обмотки;

t şi w_r – timpul curent şi viteza unghiulară a rotorului.

Система уравнений для потокосцеплений по оси α в относительных единицах имеет вид:

(3)

Система уравнений для потокосцеплений по оси β в относительных единицах имеет вид:

 

 

(4)

В системах уравнений (3) şi (4)обозначено:

x_m – индуктивное сопротивление взаимной индукции

x_s и x_r – полное индуктивное сопротивление обмотки статора и обмотки ротора;

Относительное значение электромагнитного момента может быть определено по значениям потокосцеплений и токов статора по осям α şi β:

(5)

Уравнение механического равновесия (уравнение движения) имеет вид

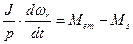(6)

где J – приведенный к ротору момент инерции;

p – число пар полюсов машины;

M_s – момент нагрузки на валу двигателя.

При питании двигателя синусоидальным напряжением составляющие напряжения по осям α и β определяются выражениями

(7)

 

где ω – угловая частота напряжения питания; U_sαm, U_sβm - амплитуды напряжения питания по осям α şi β. Если напряжение питания симметрично, то U_sαm = U_sβm = U_fm , где U_fm – амплитуда фазного напряжения трёхфазной системы..

где ω – угловая частота напряжения питания; U_m – амплитуды напряжения питания.

Схема моделирования асинхронного двигателя, реализованная в Simulink MATLAB, представлена на рисунке1.

Рис.1. Схема моделирования асинхронного двигателя

 

Блок подсистемы U_s – Ψ_s, I_s реализует решение систем уравнений (1), (2), (3) и (4). Схема моделирования подсистемы U_s – Ψ_s, I_s приведена на рисунке 2.

Напряжения питания по осям α и β (U_sα и U_sβ), в соответствии с уравнениями системы (7), воспроизводятся с помощью блоков “Sine Wave”.

Верхняя часть схемы реализует решение уравнений электрического равновесия по оси α (1). В результате на выходах блоков Int1 и Int2 вырабатываются потокосцепления по оси α Y_sα и Y_rα. После умножения их на матрицу индуктивных проводимостей с помощью блока G_s определяются токи по оси α i_sα и i_rα.

Аналогично нижняя часть реализует решение системы уравнений по оси β.

Блок подсистемы M_e реализует решение уравнения электромагнитного момента (5). Схема блока M_e представлена на рисунке 3.

Блок M – w_r решает уравнение механического (6). Схема блока M – w_r для работы на вентиляторной характеристике представлена на рисунке 4.

Блок подсистемы I_sa,I_sb,I_a,I_b,I_c преобразует систему токов в осях α, β в систему трёхфазных токов в системе естественных фазных координат. Схема блока Schema I_sa,I_sb,I_a,I_b,I_c представлена на рисунке 5.

Рис.2. Схема подсистемы U_s – Ψ_s, I_s

 

 

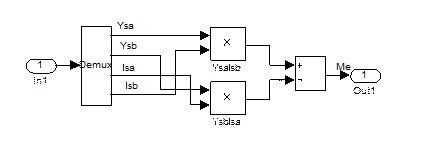
Рис.3. Схема подсистемы M_e

 

Рис.4. Схема подсистемы M – ω_r

 

 

Рис.5. Схема подсистемы I_sa,I_sb,I_a,I_b,I_c

 

2.2. Исходные данные

Для всех вариантов исходных данных общими являются: частота питающей сети f = 50 Гц, число фаз m = 3, номинальное фазное напряжение U_nf = 220 В. Варианты исходных данных приведены в таблице 1.

 

Исходные данные Таблица 1

Nr вар	Pn, кВт	In, A	nn, об/мин	rs, Ом	r’r, Ом	M, Гн	Lσs, Гн	L’σr, Гн	J*104, кгм2
	0,06	0,27				3,112	0,441	0,441	0,58
	0,09	0,41		69,2		2,03	0,271	0,288	0,59
	0,12	0,43		86,1	71,8	1,954	0,142	0,244	1,40
	0,18	0,67		56,2	52,9	1,367	0,0947	0,179
	0,25	0,86		35,4	33,0	1,140	0,067	0,138
	0,37	1,20		31,3	25,8	0,821	0,0504	0,1055
	0,55	1,58		15,0	12,7	0,709	0,0381	0,0886
	0,75	2,16		11,2	11,2	0,486	0,0272	0,0648
	1,1	2,66		8,72	4,96	0,447	0,0205	0,0316
	1,5	3,56		7,42	3,71	0,374	0,0154	0,0236
	1,5	4,10		5,91	4,73	0,308	0,0188	0,0359
	2,2	5,02		3,79	2,32	0,293	0,0106	0,0181
	3,0	6,68		2,57	1,75	0,374	0,0082	0,0136
	3,0	7,38		2,53	1,88	0,180	0,0070	0,0095
	4,0	8,59		1,55	1,23	0,196	0,0064	0,0114
	4,0	9,13		1,86	1,50	0,153	0,0056	0,0084
	5,5	11,1		1,22	0,778	0,177	0,0049	0,0049
	5,5	12,3		1,20	0,736	0,109	0,0041	0,0063
	7,5	15,1		0,700	0,480	0,139	0,0039	0,0060
	7,5	16,4		0,804	0,536	0,0896	0,0030	0,0047
	11,0	21,5		0,421	0,313	0,1042	0,0028	0,0028
	15,0	29,2		0,354	0,188	0,096	0,0021	0,0031
	18,5	35,6		0,272	0,156	0,0846	0,0017	0,0017
	22,0	41,1		0,219	0,112	0,0681	0,0014	0,0020
	30,00	55,0		0,1365	0,0723	0,0497	0,0009	0,0009
	37,00	68,5		0,1240	0,0572	0,0450	0,0009	0,0009
	45,00	81,4		0,0948	0,0474	0,0396	0,0007	0,0007
	55,00	99,3		0,0671	0,0373	0,0296	0,0006	0,0006
	75,00	135,8		0,0384	0,0215	0,0227	0,0005	0,0005
	90,00	158,5		0,0340	0,0198	0,0221	0,0004	0,0004
	5.50	10.4		1.009	0.732	0.2474	0.0054	0.0064

 

2.3. Подготовка задачи. Расчёт параметров модели.

Подготовка задачи заключается в расчёте параметров асинхронного двигателя и необходимых параметров для реализации модели в пакете Simulink MATLAB. Ниже приведен пример подготовки задачи для 31 варианта исходных данных.

Базисное значение сопротивления

Ом.

Относительные значения параметров асинхронного двигателя

; ;

;

;

;

Относительное значение полного индуктивного сопротивления обмотки статора

.

Относительное значение полного индуктивного сопротивления обмотки ротора

.

Матрица реактивных сопротивлений по осям α и β

.

Матрица реактивных проводимостей по осям α и β. Для получения матрицы проводимостей необходимо инвертировать матрицу сопротивлений. При использовании программы MATLAB инвертирование осуществляется с помощью команды g = inv(x), при использовании программы Mathcad инвертирование осуществляется с помощью команды g = x ^-1. В результате получаем матрицу проводимостей

.

Базисная мощность

Вт.

Базисный момент

Нм,

где p – число пар полюсов машины.

Базисное время

с / рад.

Базисный момент инерции

кгм².

Относительное значение момента инерции

.

Относительное значение номинального момента

Номинальное скольжение

Коэффициент момента статического сопротивления при работе на вентиляторную характеристику

2.4. Подготовка модели и выполнение исследований

Подготовка модели заключается в установке рассчитанных параметров в соответствующих блоках.

В подсистеме U_s – Ψ_s, I_s устанавливаются:

- Напряжения питания по осям α и β

- Активные сопротивления обмоток статора и ротора по осям α и β

- Матрицы реактивных проводимостей по осям α и β

В подсистеме M – ω_r устанавливаются:

- Отношение p / J^*

- Коэффициент момента статического сопротивления K_ms

Исследование заключается в снятии соответствующих осциллограмм.

Примеры снимаемых осциллограмм приведены на рисунках Рис.6 – Рис.13.

 

Рис.6. Осциллограмма процесса пуска при U=U_n и M_s=M_sn.

Зависимости M_em(t), ω_r(t).

 

 

Рис.7. Осциллограмма процесса пуска при U=0,9U_n и M_s=M_sn.

Зависимости M_em(t), ω_r(t).

 

Рис.8. Осциллограмма процесса пуска при U=0,8U_n и M_s=M_sn.

Зависимости M_em(t), ω_r(t).

 

 

 

Рис.9. Осциллограмма процесса пуска при U=U_n и M_s=1,5M_sn.

Зависимости M_em(t), ω_r(t).

 

Рис.10. Осциллограмма процесса пуска при U=U_n и M_s=M_sn.

Зависимости (I_a, I_b, I_c)(t).

 

Рис.11. Динамическая механическая характеристика

для процесса пуска при U=U_n и M_s=M_sn.

 

Рис.12. Динамическая механическая характеристика

для процесса пуска при U=U_n и M_s=1,5M_sn.

 

 

Рис.13. Годограф обобщенного вектора тока статора

для процесса пуска при U=U_n и M_s=M_sn.

 

3. Содержание отчёта

Отчёт должен содержать следующие разделы:

- Исходная математическая модель

- Схема моделирования

- Расчёт необходимых параметров модели

- Снятые осциллограммы

- Выводы

 

4. Контрольные вопросы

4.1. Как изменится процесс пуска при уменьшении или увеличении активного сопротивления обмотки ротора?

4.2. Как влияет величина напряжения питания на пусковые и рабочие характеристики асинхронного двигателя?

4.3. Как влияет несимметрия питания на рабочие характеристики асинхронного двигателя?

4.4. Как на основании полученных результатов можно определить максимальное значение электромагнитного момента и тока обмотки статора?