ОПИСАНИЕ ТЕХНИЧЕСКИХ СРЕДСТВ ВЫПОЛНЕНИЯ РАБОТЫ

СОДЕРЖАНИЕ

 

1. Цель работы 3

2. Краткие теоретические сведения 3

3. Описание технических средств выполнения работы 5

4. Порядок выполнения теоретических расчетов 5

5. Порядок выполнения экспериментальных исследований 6

6. Содержание отчета о выполнении лабораторной работы 7

7. Контрольные вопросы 7

Библиографический список 8

 

 

ЦЕЛЬ РАБОТЫ

 

Изучить применение метода гармонической линеаризации к исследованию автоколебаний в нелинейных системах автоматического управления (НСАУ).

 

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

 

Метод гармонической линеаризации служит для при­ближенного определения периодических решений (автоколебаний) и устой­чивости нелинейных систем любого порядка и по идее близок к методу гармонического баланса Н. М. Кры­лова и Н. Н. Боголюбова. Идея метода состоит в отыскании такой системы, свойства которой были бы близки к некоторым свойствам изучаемой нелинейной системы [1, 2].

Метод гармонической линеаризации заключается в отыскании периодического решения на входе нелинейного элемента, разложении сигнала на выходе нелинейного элемента в ряд Фурье и его замене первой гармоникой. Такая замена справедлива, если система автоматического управления является фильтром низких частот, хорошо гасящим колебания высших гармоник.

Рассматриваемый приближенный метод является мощным средством исследования нелинейных систем автоматического управления в смысле простоты и до­вольно большой универсальности его аппарата в применении к самым разно­образным нелинейностям.

Пусть рассматривается нелинейный элемент, заданный функцией вида

у =F(х), (1)
где

x = a sin y, y=w t. (2)

Тогда

x '= a w cos y. (3)

 

Разложив функцию в правой части (1) в ряд Фурье, получим

 

 

 

 

 

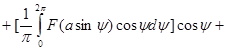
+ высшие гармоники. (4)

 

Положим

 

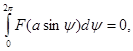(5)

 

что означает отсутствие постоянной составляющей в данном разложении.

Если принять во внимание, что из (2) и (3)

 

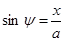и ,

 

 

то формулу (4) при условии (5) можно будет записать в виде

 

 

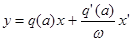+ высшие гармоники, (6)

где q (а) и q '(а) - коэффициенты гармонической линеаризации, определяемые формулами:

 

 

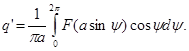
Итак, нелинейное выражение (1) при x = a sinw t заменяется выра­жением (6), которое с точностью до высших гармоник аналогично линейно­му. Эта операция и называется гармонической линеаризацией. Для разных амплитуд периодических процессов коэффициенты выражения (6) будут различны по величине. Это очень важное обстоятельство является существенным отличием гармонической линеаризации, по сравнению с обыч­ным способом линеаризации, приводящим к чисто линейным выражени­ям. Указанное обстоя­тельство и позволит путем применения к выражению (6) линейных мето­дов исследования проанализировать основные свойства нелинейных систем, которые не могут быть обнаружены при обычной линеаризации. Выражения q (а) и q '(а) для типовых нелинейностей приводятся в учебниках и справочниках по теории автоматического управления.

В случае, если нелинейность располагается в 1 и 3 квадрантах (не имеет гистерезисной петли), то q '=0.

Для применения метода гармонической линеаризации НСАУ приводится к виду:

 

 

Рисунок 1 – Структурная схема приведенной нелинейной системы

 

На рисунке 1 W_ЛЧ(s) – передаточная функция линейной части НСАУ;

W_НЭ(а) – приближенная передаточная функция нелинейного элемента, описанного выражением (1).

Согласно (6) W_НЭ(а) будет иметь вид

 

. (7)

 

Известно [1], что незатухающие синусои­дальные колебания с постоянной амплитудой в замкнутой системе могут опреде­ляться согласно частотному критерию устойчивости Найквиста прохожде­нием амплитудно-фазовой характеристики разомкнутой системы через точку (-1, j0), т.е. равенством

 

W_ЛЧ(jw)W_НЭ(а)=-1. (8)

 

Это и будет в данном случае условием существования периодического решения для замкнутой нелинейной системы, которое принимается приближенно синусоидальным.

С учетом (7) и замены s на jw равенство (8) можно записать в виде

 

, (9)

 

 

где правая часть будет вещественной в случае когда q'(а)=0.

Левая часть уравнения (9) представляет собой ампли­тудно-фазовую характеристику линейной части системы, а правая — обрат­ную амплитудно-фазовую характеристику нелинейного звена (для первой гармоники), взятую с обратным знаком. Решение этого уравнения можно получить графически как точку пересечения указанных двух характеристик. В точке пересечения из кривой W_ЛЧ(jw) определяем значение частоты, а из кривой -1/ q (а) - величину амплитуды искомого периодического решения.

 

ОПИСАНИЕ ТЕХНИЧЕСКИХ СРЕДСТВ ВЫПОЛНЕНИЯ РАБОТЫ

 

Построение годографов исследуемых НСАУ производится с использованием ПЭВМ и предлагаемых преподавателем пакетов прикладных программ.