Целенаправленной является система, стремящаяся к достижению некоторой цели. Целенаправленную систему можно описать не прямо, а с помощью некоторой задачи принятия решений, т.е. систему S Ì Х ´ Y определяют таким образом, чтобы пара (x, y) принадлежала S тогда и только тогда, когда у является решением задачи принятия решений, задаваемой элементом х.
Рассмотрим два частных случая задачи принятия решений.
1. Общая задача оптимизации.
Пусть g: X ® V, некоторая функция, отображающая произвольное множество Х в линейное или частично упорядоченное множество 
Тогда общая задача оптимизации состоит в следующем.
Для данного подмножества Xf Í X найти такое 
что для всех
где Х – множество возможных решений;
Xf – множество допустимых решений;
g – целевая функция;
V – множество оценок.
Тогда общая задача оптимизации задается парой (g, Xf). Элемент 
удовлетворяющий условию 
при всех х Î Xf называется решением задачи оптимизации, заданной парой (g, Xf).
Часто функцию g определяют с помощью двух функций:
Р: X ® Y и G: X ´ Y ® V,
g(x) = G(x, P(x)).
В этом случае Р называют выходной функцией или моделью управления, а G – критерием качества или оценочной функцией. При этом задача оптимизации задается тройкой (P, G, Xf) или парой (P, G), если Xf = Х.
Функция Р здесь называется моделью объекта управления вследствие того, что задача оптимизации, задаваемая тройкой (P, G, Xf), определяется относительно системы, которой нужно управлять и которая описывается функцией Р.
2. Общая задача удовлетворения.
Пусть Х и W - произвольные множества, а g – функция из Х ´ W в линейно упорядоченное множество Пусть также t - некоторая функция из W в V. Тогда задача удовлетворения состоит в следующем.
Для заданных Xf Í X найти такой элемент что для всех w Î W
где W - множество неопределенности;
t - функция, задающая уровень удовлетворения;
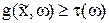- критерий удовлетворения.
Тогда общая задача удовлетворения определяется четверкой (g, t, Xf, W), а элемент удовлетворяющий критерию 
при всех w Î W, является решением задачи удовлетворения, задаваемой четверкой (g, t, Xf, W).
Множество неопределенности W называют также множеством возмущений, т.к. оно представляет собой множество различных воздействий, которые сказываются на поведении системы.
Функция t определяет нижний предел допустимого или приемлемого качества системы.
Целевая функция g может быть задана через выходную функцию P: X ´ W ® Y и оценочную функцию G: X ´ W ´ Y ® V
g(x, w) = G(x, w, P(x, w)).
В этом случае W определяет множество всевозможных воздействий, которые могут сказаться на исходе принятого решения х.
Теперь можно определить систему принятия решений.
Система S Ì Х ´ Y называется системой принятия решений, если найдутся такое семейство задач принятия решений Dx, х Î X, решения которых принадлежат множеству Z, и такое отображение T: Z ® Y, что для любого х Î X и y Î Y пара (х, у) принадлежит системе S тогда и только тогда, когда найдется такое z Î Z, что z является решением задачи Dx, а T(z) = y.
Во многих случаях выходные величины системы совпадают с решениями задачи принятия решений (Z = Y), а отображение Т тождественно.
В общем случае понятие цели и целенаправленного поведения может остаться неформализованным. Однако, если формализация целенаправленного поведения возможна, она неизбежно приводит к описанию общей задачи принятия решений. При этом формализованная цель определяется некоторой задачей принятия решений, а достижение цели означает, что соответствующая задача принятия решений решена.
Кроме рассмотренных классов систем в ОТС-МТ рассматриваются вопросы устойчивости и реализации систем, а также декомпозиция и соединение систем.