Теория систем и системный анализ
Общая теория систем М. Месаровича и Я. Такахары
Общая теория систем (ОТС) призвана дать средства описания и формальный метод моделирования для отражения и исследования максимально разнообразных объектов, процессов и явлений реального мира.
В данном случае мы рассматриваем системный подход и формальные методы, предложенные М. Месаровичем и Я. Такахарой.
Особенности ОТС Месаровича и Такахары (ОТС-МТ) заключаются в теоретико-множественном подходе к описанию систем, аксиоматическом введении различных свойств систем и их строгом математическом исследовании.
Определение системы в ОТС-МТ
Формальное определение системы задается следующим образом: предполагается, что задано семейство множеств
V = {Vi: i Î I},
где I – множество индексов.
Система S на V задается как некоторое отношение декартова произведения ´ V:
S Ì ´{Vi: i Î I}.
Множества Vi, i Î I, декартова произведения ´Vi называются объектами системы S. Например, система вход-выход или “ черный ящик ” с двумя объектами – входом Х и выходом Y имеет вид:
S Ì X ´ Y,
где X = ´{Vi: i Î Ix}, Y = ´{Vi: i Î Iy}, Ix È Iy = I и Ix Ç Iy = Æ.
Если S является функцией S = X ® Y, то система называется функциональной.
Таким образом, система S:
- задается отношением (S Ì X ´ Y) и не обязательно является функциональной (S = X ® Y), т.к. могут быть многозначные соответствия между элементами объектов X и Y;
- не может быть равна декартову произведению объектов (S = X ´ Y), т.к. это соответствует полной дезорганизованности и уничтожению системы.
Задание внутренней структуры системы возможно путем введения структуры для элементов vi Î Vi и введения структуры для самих объектов Vi. В первом случае получаем абстрактную временную систему, а во втором – алгебраическую систему.
Формальное определение временной системы задается следующим образом: пусть элементы объекта V есть функции (функциональные отображения) вида v: Tv ® Av, где Т – индексирующее множество, а А – алфавит объекта. Такой объект V называется функциональным объектом. Если множество элементов Tv линейно упорядочено, то его называют множеством моментов времени. Функции, определенные на множествах моментов времени, называются абстрактными функциями времени. Объект, элементами которого являются временные функции, называется временным объектом, а системы, определенные на временных объектах, - временными системами.
Например, временная система вход-выход задается следующим образом: пусть А и В – произвольные множества, Т – множество моментов времени, АТ и ВТ – множества всевозможных отображений из Т в А и В соответственно и Х Ì АТ, Y Ì ВТ. Тогда временной системой S над Х и Y называется отношение на Х и Y вида
S Ì X ´ Y Ì АТ ´ ВТ.
Формальное определение алгебраической системы задается следующим образом: для объекта V определяют одну или несколько операций, относительно которых V становится алгеброй. В простейшем случае определяется бинарная операция r: V ´ V ® V и предполагается, что существует обычно конечное подмножество W Ì V такое, что любой элемент v Î V можно получить путем применения операции r к элементам из W и уже порожденным элементам из V. В этом случае r называется производящей функцией, W – множеством производящих элементов или алфавитом объекта, его элементы – символами, а элементы объекта V – словами. Если r есть операция конкатенации (сочленения), то слова – это просто последовательности элементов алфавита W, а V – это язык.
Определение состояния системы задается следующим образом: пусть для системы S задано произвольное множество С, а частичная функция r: (C ´ X) ® Y такова, что
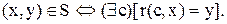
Тогда С называется объектом глобальных состояний системы, а его элементы – глобальными состояниями системы. Частичная функция r, означающая, что не для каждого значения (с, х) Î C ´ X существует значение у Î Y, называется частичной глобальной реакцией системы S. Если функция r является полной, то она называется глобальной реакцией системы S, т.е.
r: C ´ X ® Y.
Начальным состоянием С0 и начальной реакцией r0 системы S называются объект глобальных состояний и глобальная реакция этой системы в момент времени t0:
r0: C0 ´ X0 ® Y,
удовлетворяющие условию 
Подобным образом можно определить состояние Ct и реакцию системы rt в момент времени t:
rt: Ct ´ Xt ® Y,
что 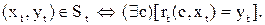
Тогда семейство всех состояний системы есть
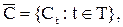
а семейство всех реакций системы есть