При уровне значимости a=0.05 определите статистическую достоверность влияния фактора А на динамику величины Х.
| № испытания | A1 | A2 | A3 | A4 |
РЕШЕНИЕ
Число выборок m=6, значения во всех выборках n=22
| № испытания | A1 | A2 | A3 | A4 | Σ | n |
Выборочное среднее:
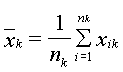
Сумма квадратов отклонений выборочных средних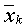 
от общего среднего 
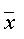(сумма квадратов отклонений между группами):
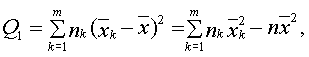
Сумма квадратов отклонений наблюдаемых значений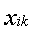 
от выборочной средней 
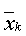(сумма квадратов отклонений внутри групп):
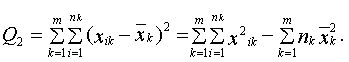
Общая сумма квадратов отклонений наблюдаемых значений 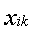от общего среднего
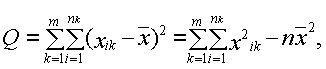
| № | А ср. | А ср.2 | А ср.2 * n |
| 4,25 | 18,0625 | 72,25 | |
| 10,66667 | 113,7778 | 341,3333 | |
| 9,75 | 95,0625 | 380,25 | |
| 7,5 | 56,25 | ||
| 5,75 | 33,0625 | 132,25 | |
| 6,333333 | 40,11111 | 120,3333 | |
| Σ | 7,272727 | 1271,417 |
Тогда Q = 330,36
Q1 = 107,18
Q2 = Q – Q1 = 222,58
В качестве критерия необходимо воспользоваться критерием Фишера:
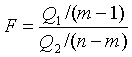
F = 1,549
Табличное значение критерия Фишера для заданном уровне значимости 0,05 равен 3,8564.
Так как расчетное значение критерия Фишера меньше табличного, нет оснований считать, что независимый фактор оказывает влияние на разброс средних значений.
Задача 3. Двухфакторный дисперсионный анализ
При уровне значимости a=0.05 определите статистическую достоверность влияния фактора А и фактора В на динамику величины Х.
| B1 | B2 | B3 | B4 | |
| A1 | ||||
| A2 | ||||
| A3 | ||||
| A4 | ||||
| A5 |
РЕШЕНИЕ
При двухфакторном дисперсионном анализе изучается влияние, которое оказывают два качественных признака (факторы A и B) на некоторый количественный результат (отклик). Весьма типична ситуация, когда второй фактор (фактор B) является мешающим: он включается в рассмотрение по той причине, что мешает обнаружить и оценить влияние фактора A.
Пусть фактор A имеет k уровней A1,..., Ak, а фактор B - n уровней B1,...,Bn. Предполагается, что измеряемая величина x есть результат действия факторов A и B и случайной составляющей e:
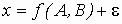
Принимается аддитивная и независимая модель действия факторов:
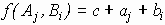причем
, 
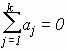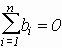
Последние два условия всегда можно выполнить смещением величин aj и bi и изменением величины c; величины aj и bi называются вкладами факторов.
Проведем двухфакторный дисперсионный анализ при помощи пакета анализа программы Excel:
| ИТОГИ | Счет | Сумма | Среднее | Дисперсия |
| A1 | 9,5 | |||
| A2 | 10,5 | |||
| A3 | 11,25 | 30,91666667 | ||
| A4 | 10,25 | 84,25 | ||
| A5 | 8,75 | 0,916666667 | ||
| B1 | ||||
| B2 | 11,2 | 32,7 | ||
| B3 | 8,8 | 45,2 | ||
| B4 | 14,2 | 33,7 |
| Дисперсионный анализ | ||||||
| Источник вариации | Сумма квадратов отклонений | Степени свободы | Среднеквадратическое отклонение | Отношение ср.кв.откл. фактора к ср.кв.откл. погрешности | P-Значение | F критическое |
| А | 14,7 | 3,675 | 0,0985 | 0,9809 | 3,259 | |
| В | 182,55 | 60,85 | 1,631 | 0,2343 | 3,49 | |
| Погрешность | 447,7 | 37,308 | ||||
| Итого | 644,95 |
Так как расчетное значение 0,98 и 0,23 больше заданного уровня значимости независимый фактор оказывает существенное влияние на разброс средних значений.