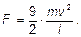Закон изменения импульса для одной материальной точки.
Второй закон Ньютона для материальной точки, когда на нее действует постоянная сила, может быть переписан в виде закона изменения импульса
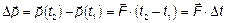
- приращение импульса материальной точки равно импульсу силы (произведению силы на время, за которое импульс точки изменился на 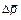 ), действующей на материальную точку.
), действующей на материальную точку.
3.1. Величина импульса материальной точки равна 100 кг∙м/с. Под действием постоянной силы направление вектора импульса изменяется на противоположное за две секунды. Вычислите величину силы.
3.2. Величина импульса материальной точки равна 100 кг∙м/с. Под действием постоянной силы за время 1,4 секунды вектор импульса повернулся на 900. Вычислите величину силы.
Система материальных точек.
Импульс системы материальных точек – это сумма (конечно векторная) импульсов материальных точек:
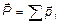 .
.
Производная импульса системы материальных точек по времени равна сумме всех сил, действующих на систему, и, с учетом третьего закона Ньютона, равна сумме внешних сил, действующих на систему материальных точек:
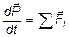 .
.
3.3. В лабораторной системе отсчета модули импульсов двух материальных точек равны 3 кг∙м/с и 4 кг∙м/с. Направления импульсов составляют прямой угол. Вычислите модуль импульса системы этих материальных точек в лабораторной системе отсчета.
3.4. Система состоит из двух тел. Известны зависимости от времени импульсов этих тел 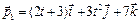 и
и  . Сохраняется ли импульс системы?
. Сохраняется ли импульс системы?
3.5. Система состоит из двух тел. Известны зависимости от времени импульсов этих тел 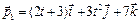 и
и  . Сохраняются ли какие - либо проекции импульса системы на оси координат?
. Сохраняются ли какие - либо проекции импульса системы на оси координат?
3.6. Система состоит из двух тел. Известны зависимости от времени импульсов этих тел 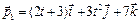 и
и  . Найдите сумму внешних сил, приложенных к телам, и вычислите ее величину для t = 1/6 с.
. Найдите сумму внешних сил, приложенных к телам, и вычислите ее величину для t = 1/6 с.
Сохранение импульса системы взаимодействующих тел.
Из закона изменения импульса 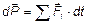 следует, что если
следует, что если 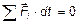 , то
, то 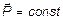 .
.
Для проекций на выделенное направление X можно утверждать, что из 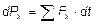 следует
следует  , если
, если 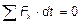 .
.
3.7. Платформа движется по горизонтальным рельсам в положительном направлении координатной оси X со скоростью 1м/с. Человек, масса которого равна массе платформы, находится на платформе и сначала покоится относительно нее. Затем человек разгоняется и покидает платформу со скоростью 2м/с относительно платформы в положительном направлении координатной оси X. Вычислите скорость пустой платформы.
3.8. Платформа движется по горизонтальным рельсам в положительном направлении координатной оси X со скоростью 1м/с. Человек, масса которого равна массе платформы, находится на платформе и сначала покоится относительно нее. Затем человек разгоняется и покидает платформу со скоростью 2м/с относительно платформы в отрицательном направлении координатной оси X. Вычислите скорость пустой платформы.
3.9. Платформа движется по горизонтальным рельсам в положительном направлении координатной оси X со скоростью 1м/с. Человек, масса которого равна массе платформы, находится на платформе и сначала покоится относительно нее. Затем человек разгоняется и покидает платформу с горизонтальной скоростью 2м/с относительно платформы в направлении перпендикулярном координатной оси X. Вычислите скорость пустой платформы.
3.10. Тележка с песком движется по горизонтальным прямолинейным рельсам со скоростью 10 м/с. В дне тележки образовалась дыра, песок стал высыпаться, и через некоторое время масса тележки с песком уменьшилась в два раза. Вычислите скорость тележки для этого момента времени. Трением о рельсы и сопротивлением воздуха пренебречь.
3.11. Пустая тележка движется по горизонтальным прямолинейным рельсам со скоростью 10 м/с. По ходу движения тележки, над рельсами на достаточной высоте закреплен бункер с песком. В момент прохождения тележки под бункером из него в тележку высыпался песок, масса которого равна массе пустой тележки. Вычислите конечную скорость тележки. Трением о рельсы и сопротивлением воздуха пренебречь.
3.12. На покоившейся тележке массы M стояли два человека одинаковой массы m. Затем они покинули тележку, разогнавшись вдоль рельсов до скорости 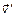 относительно тележки, один раз одновременно, другой раз последовательно друг за другом. В каком случае скорость тележки будет больше и во сколько раз?
относительно тележки, один раз одновременно, другой раз последовательно друг за другом. В каком случае скорость тележки будет больше и во сколько раз?
Уравнение движения тела с изменяющееся массой – уравнение Мещерского.

m – масса,  - ускорение тела в рассматриваемый момент времени,
- ускорение тела в рассматриваемый момент времени, 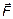 - сумма всех внешних сил,
- сумма всех внешних сил, 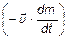 - реактивная сила.
- реактивная сила.
3.13. Допустим, что каждую секунду из ракеты вылетает 100 кг отработанного топлива со скоростью 500 м/с (относительно ракеты). Вычислите величину силы, действующей на ракету со стороны вылетающего топлива.
3.14. Допустим, что скорость, с которой вылетает из ракеты топливо (в системе отсчета «ракета»), равна 500 м/с. Ракета стартует с нулевой начальной скоростью в отсутствие внешних сил. Вычислите величину скорости ракеты в момент, когда масса ракеты уменьшится приблизительно в 2,7 раза по сравнению со стартовой.
3.15. Стартовая масса двухступенчатой ракеты равна M = 25,5т. Масса корпуса первой ступени равна m01 = 2т, масса топлива в ней m1 = 20т. После сжигания 20т топлива первая ступень отбрасывается и включается вторая ступень. Скорость истечения топлива в системе отсчета “ракета” равна u = 1км/с. Найдите скорость v1 ракеты в момент отделения первой ступени.
3.16. Стартовая масса двухступенчатой ракеты равна M = 25,5т. Масса корпуса первой ступени равна m01 = 2т, масса топлива в ней m1 = 20т. Масса корпуса второй ступени равна m02 = 0,5т, масса топлива в ней m2 = 3т. После сжигания 20т топлива первая ступень отбрасывается и включается вторая ступень. Скорость истечения топлива в системе отсчета “ракета” равна u = 1км/с. Найдите скорость v2 ракеты после использования всего топлива.
3.17. Стартовая масса одноступенчатой ракеты равна M = 25,5т. Масса корпуса равна m0 = 2,5т, масса топлива m = 23т. Скорость истечения топлива в системе отсчета “ракета” равна u = 1км/с. Найдите скорость v ракеты после использования всего топлива. Результат вычислений сравните с ответом в предыдущей задаче.
Центр масс. Система отсчета центра масс.
Центром масс системы материальных точек называется точка пространства, радиус-вектор которой находится по формуле
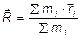 .
.
Соответственно скорость центра масс равна
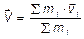 .
.
Системой отсчета центра масс (Ц-системой) называется такая система отсчета, относительно которой покоится центр масс рассматриваемой системы частиц и, которая движется поступательно относительно инерциальной системы отсчета.
3.18. Две материальные точки одинаковой массы движутся со скоростями 3 м/с и 4 м/с во взаимно перпендикулярных направлениях. Вычислите модуль скорости V центра масс системы этих точек.
3.19. В лабораторной системе отсчета модули импульсов двух материальных точек равны 3 кг∙м/с и 4 кг∙м/с. Направления импульсов составляют прямой угол. Вычислите модуль импульса P системы этих материальных точек в лабораторной системе отсчета.
3.20. В лабораторной системе отсчета модули импульсов двух материальных точек одинаковы и равны 4 кг∙м/с. Векторы импульсов сонаправлены и лежат на прямой, проходящей через обе материальные точки. Вычислите модуль импульса 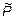 системы этих материальных точек в системе отсчета центра масс.
системы этих материальных точек в системе отсчета центра масс.
3.21. В лабораторной системе отсчета модули импульсов двух материальных точек одинаковы и равны 2кг∙м/с. Векторы импульсов противонаправлены и лежат на прямой, проходящей через обе материальные точки. Вычислите модуль импульса 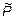 системы этих материальных точек в системе отсчета центра масс.
системы этих материальных точек в системе отсчета центра масс.
3.22. В лабораторной системе отсчета модули импульсов двух материальных точек равны 2кг∙м/с и 5кг∙м/с соответственно. Векторы импульсов противонаправлены и лежат на прямой, проходящей через обе материальные точки. Вычислите модуль импульса 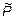 системы этих материальных точек в системе отсчета центра масс.
системы этих материальных точек в системе отсчета центра масс.
3.23. В лабораторной системе отсчета модули импульсов двух материальных точек равны 3 кг∙м/с и 4 кг∙м/с. Направления импульсов составляют прямой угол. Вычислите модуль импульса 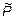 системы этих материальных точек в системе отсчета центра масс.
системы этих материальных точек в системе отсчета центра масс.
Использование Ц-системы отсчета для представления движения системы материальных точек в виде суммы движения системы точек как целого и внутреннего движения.
3.24. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, сонаправлены и равны соответственно v и 3 v. Найдите величину F силы натяжения нити.
3.25. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, противонаправлены и равны соответственно v и 3 v. Найдите величину F силы натяжения нити.
3.26. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, сонаправлены и равны соответственно 3 v и 5 v. Найдите величину F силы натяжения нити.
3.27. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, противонаправлены и равны соответственно 3 v и 5 v. Найдите величину F силы натяжения нити.
3.28. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, сонаправлены и равны соответственно 2 v и 4 v. Найдите величину F силы натяжения нити.
3.29. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, противонаправлены и равны соответственно 2 v и 4 v. Найдите величину F силы натяжения нити.
3.30. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, сонаправлены и равны соответственно 4 v и 6 v. Найдите величину F силы натяжения нити.
3.31. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, противонаправлены и равны соответственно 4 v и 6 v. Найдите величину F силы натяжения нити.
3.32. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, сонаправлены и равны соответственно v/ 2 и 5 v/ 2. Найдите величину F силы натяжения нити.
3.33. Две небольшие одинаковые шайбы массой m каждая, связаны нерастяжимой нитью длины l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорости шайб перпендикулярны нити, противонаправлены и равны соответственно v/ 2 и 5 v/ 2. Найдите величину F силы натяжения нити.
Ответы
3.1 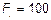 Н.
Н.
3.2 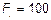 Н.
Н.
3.3  кг∙м/с.
кг∙м/с.
3.4 Нет.
3.5 Сохраняются на X и Y.
3.6  ;
;
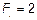 Н.
Н.
3.7 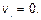
3.8 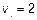 м/с.
м/с.
3.9  м/с.
м/с.
3.10 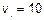 м/с.
м/с.
3.11  м/с.
м/с.
3.12 Одновременно  ;
;
последовательно 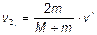 ;
;

3.13 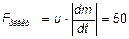 кН.
кН.
3.14 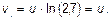
3.15 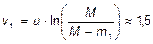 км/ч.
км/ч.
3.16  км/с.
км/с.
3.17  км/с.
км/с.
3.18 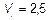 м/с.
м/с.
3.19  кг∙м/с.
кг∙м/с.
3.20 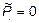 .
.
3.21 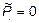 .
.
3.22 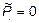 .
.
3.23 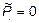 .
.
3.24 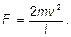
3.25 
3.26 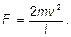
3.27 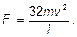
3.28 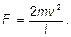
3.29 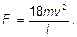
3.30 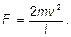
3.31 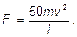
3.32 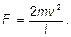
3.33