ТРАНСПОРТНОЕ ОБЕСПЕЧЕНИЕ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ
проф. Скороходов А.Н., доц. Уваров В..П.
Цель задания – освоить методы решения транспортных задач при организации перевозок сельскохозяйственных грузов.
Задание. Производственную ситуацию, соответствующую Вашему варианту, выберите из таблицы1.
Составьте план грузоперемещений, обеспечив минимум транспортных затрат на перевозку всего груза.
1. Типы инженерных задач при организации перевозок сельскохозяйственных грузов
Интенсификация сельскохозяйственного производства предполагает возрастание роли транспорта. На долю транспортных операций приходится 30-40 % всех затрат денежных средств, необходимых для производства сельскохозяйственной продукции.
При оперативном планировании часто возникает необходимость определить потребность в транспортных средствах для перевозки определенного груза на заданное расстояние в установленные агротехнические сроки, или необходимо перевезти большое количество  однородного груза из ряда (m) пунктов отправления в несколько (n) пунктов назначения, используя однотипные транспортные средства. Здесь возможно m х n вариантов организации грузопотоков между пунктами отправления и назначения. Подобные производственные ситуации могут быть:
однородного груза из ряда (m) пунктов отправления в несколько (n) пунктов назначения, используя однотипные транспортные средства. Здесь возможно m х n вариантов организации грузопотоков между пунктами отправления и назначения. Подобные производственные ситуации могут быть:
- при организации перевозок: зерна, картофеля, свеклы, силоса, сена. соломы и т.д. с полей к местам хранения или складирования продукции;
- транспортировка органических или минеральных удобрений от ферм или мест складирования на поля и т.д.
Для выбора лучшего варианта плана перевозок необходим оценочный критерий. Чаще всего для этого используют минимум эксплуатационных затрат или минимум грузоперемещений.Для получения минимума затрат при перевозке однородного груза однотипными транспортными средствами необходимо обеспечить минимум грузоперемещений. Тогда общая формулировка поставленной задачи может быть дана в следующей форме.
Пусть имеется m пунктов сосредоточение однородного груза, который необходимо перевезти на n пунктов назначения. Количество груза на i- ом пункте отправления (i=1,2,3…m) равно Qi тонн. Потребность j-го пункта назначения в этом грузе (j=1,2,3…n) составляет Вj 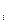
 тонн. Расстояние между каждым пунктом отправления и назначения груза известно. Для перевозки груза используются однотипные транспортные средства (тракторные тележки, бортовые автомобили, самосвалы и т.д.).
тонн. Расстояние между каждым пунктом отправления и назначения груза известно. Для перевозки груза используются однотипные транспортные средства (тракторные тележки, бортовые автомобили, самосвалы и т.д.).
Таблица 1
Производственная ситуация
| Вариант задания | Валовый сбор зерна, т | Расстояния от полей до хранилищ, км. | ||||||||
| 1-5 | 1-3000 | |||||||||
| 2-5000 | ||||||||||
| 3-4000 | ||||||||||
| Емкость хранилищ,т | ||||||||||
| Вариант задания | Валовый сбор картофеля, т | Расстояния от полей до хранилищ, км. | ||||||||
| 6-10 | 1-500 | |||||||||
| 2-500 | ||||||||||
| 3-300 | ||||||||||
| 4-300 | ||||||||||
| Емкость хранилищ,т | ||||||||||
| Вариант задания | Валовый сбор сах.свеклы, т | Расстояния от полей до хранилищ, км. | ||||||||
| 11-16 | 1-300 | |||||||||
| 2-500 | ||||||||||
| 3-200 | ||||||||||
| Емкость хранилищ,т | ||||||||||
| Вариант задания | Емкость хранилищ орг. удобрений,т | Расстояния от хранилищ до полей, км. | ||||||||
| 17-20 | 1-7000 | |||||||||
| 2-5000 | ||||||||||
| 3-8000 | ||||||||||
| Норма внесения на поля,т | ||||||||||
| Вариант задания | Емкость хранилищ мин. удобрений,т | Расстояния от хранилищ до полей, км. | ||||||||
| 21-25 | 1-400 | |||||||||
| 2-400 | ||||||||||
| 3-200 | ||||||||||
| Норма внесения на поля,т | ||||||||||
Требуется составить план перевозок, т.е. определить количество груза, перевозимого с i-го пункта на j-ый, чтобы обеспечить минимум грузоперемещений (а следовательно и эксплуатационных затрат) на перевозку всего груза.
Соотношение количества груза во всех пунктах его отправления (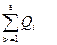 ) и потребностей в нем всех пунктов назначения (
) и потребностей в нем всех пунктов назначения (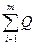 ) и потребностей в нем всех пунктов назначения (
) и потребностей в нем всех пунктов назначения (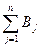 ) может быть различным, а именно:
) может быть различным, а именно:
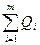 =
= 
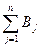 (1)
(1)
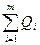 >
> 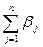 (2)
(2)
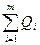 <
< 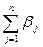 (3)
(3)
Первое условие означает, что общие потребности пунктов назначения в грузе равны его запасам на пунктах отправления. Неравенство (2) означает, что запасы груза превалируют над его потребностями, а неравенство (3) выражает обратное условие.
Транспортная задача, содержащая условие (1), называется задачей закрытого типа. Если же условие задачи отвечает соотношению (2) или (3), то она относится к числу транспортных задач открытого типа.
Часто возникает более сложная задача составления плана перевозок совокупности неоднородных грузов разнотипными транспортными средствами в пределах установленных сроков. При этом необходимо учитывать, что производственные возможности каждого вида транспортировке различных грузов различны.
Целью решения таких задач является определение объема транспортных работ, выполненных каждым видом транспортных средств, при котором значение избранного критерия оптимальности достигает минимума. Инженерный расчет сводится к распределению заданного объема неоднородной совокупности транспортных работ по имеющимся транспортным агрегатам. Задачи подобного типа относятся к категории распределительных задач.
2. Математическая формулировка транспортной задачи
Обозначим через  х
х  искомое количество груза., перевозимого с i-го пункта на j-ый. Общая величина грузоперемещений Z, которую предстоит сделать при транспортировке всего заданного объема груза будет
искомое количество груза., перевозимого с i-го пункта на j-ый. Общая величина грузоперемещений Z, которую предстоит сделать при транспортировке всего заданного объема груза будет
Z= 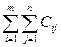 X
X  . (4)
. (4)
По условию задачи необходимо найти такой план перевозок, т.е. подобрать такие значения х  , чтобы величина Z была минимально возможной.
, чтобы величина Z была минимально возможной.
Z= 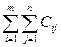 X
X  =min (5)
=min (5)
Уравнение (5) выражает основное условие задачи, цель поиска, поэтому его называют функцией цели.
При минимизации уравнения (5) из всего множества значений х  , должны быть выбраны только определенные значения, которые удовлетворяют остальным требованиям задачи. Прежде всего диапазон возможных значений х
, должны быть выбраны только определенные значения, которые удовлетворяют остальным требованиям задачи. Прежде всего диапазон возможных значений х  ограничен областью положительных чисел. Это следует из физического существа величины х
ограничен областью положительных чисел. Это следует из физического существа величины х  . Отрицательное значение х
. Отрицательное значение х  означало бы транспортировку уже перевезенного груза в обратном направлении, т.е. с j-го пункта на i-ый, что противоречит смыслу задачи.
означало бы транспортировку уже перевезенного груза в обратном направлении, т.е. с j-го пункта на i-ый, что противоречит смыслу задачи.
Это ограничение может быть записано так 
х 
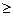 0 i=1, m, j=1,
0 i=1, m, j=1, 
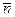 .
.  (6)
(6)
Кроме того из условия задачи следует, что общее количество груза, перевозимого с i-го пункта отправления во все пункты назначения, равно запасам груза на этом пункте, т.е.
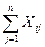 =Q
=Q 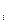 i=1,
i=1, 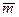 . (7)
. (7)
Суммирование здесь идет по всем возможным маршрутам, исходящим из i-го пункта, а их число потенциально равно n.
По условию задачи поступление груза из всех пунктов его отправления в j-ый пункт ограничено потребностями в грузе этого пункта, т.е.
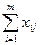 = B
= B 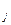 j=1,
j=1, 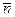 . (8)
. (8)
Суммирование здесь происходит по всем возможным маршрутам, заканчивающимся в j-ом пункте, а их число потенциально равно m.
Равенства (7) и (8) обусловлены тем, что по условию задачи общие запасы груза на пунктах отправления равны общим потребностям в нем всех пунктов назначения.
Других ограничений, кроме отмеченных, которые было бы необходимо соблюсти при решении задачи, в ее условии нет.
Таким образом, математическая формулировка транспортной задачи закрытого типа (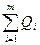 =
= 
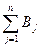 ) имеет вид:
) имеет вид:
Найти минимум функций цели
Z= 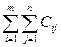 X
X  =min.
=min.
При следующих ограничениях:
1. х 
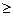 0
0
2. 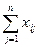 =Q
=Q 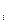
3. 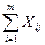 =B
=B 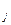
В открытой модели транспортной задачи запасы груза на пунктах отправления не равны потребностям в нем пунктов назначения,
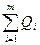 ≠
≠ 
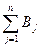 .
.
В соответствии с условием уравнение функции цели для транспортной задачи обоих типов одинаково.
В тех случаях, когда в пунктах отправления грузов имеется больше, чем требуется в пунктах назначения, т.е. 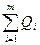 =
= 
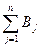 система уравнений оказывается несовместной, так как часть груза должна оставаться на пунктах отправления. Поэтому условие задачи (7) следует писать так:
система уравнений оказывается несовместной, так как часть груза должна оставаться на пунктах отправления. Поэтому условие задачи (7) следует писать так:
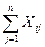 ≤ Q
≤ Q 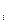 i=1,
i=1, 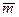 . (9)
. (9)
В этом случае с i-го пункта может быть вывезен или весь груз или только часть его.
При избытке груза на пунктах его отправления, по сравнению с общим объемом перевозок во все пункты назначения, на j-ый пункт поступит точно B 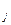 тонн груза. Следовательно, условие (8) останется неизменным.
тонн груза. Следовательно, условие (8) останется неизменным.
При недостатке запасов груза, т.е. при 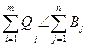 общее количество груза, перевозимого с i-го пункта отправления во все пункты назначения, равно запасам груза на этом пункте, т.е. условие (7) останется неизменным.
общее количество груза, перевозимого с i-го пункта отправления во все пункты назначения, равно запасам груза на этом пункте, т.е. условие (7) останется неизменным.
Соотношение общего объема груза, поступившего на j-ый пункт по всем маршрутам, и потребностей этого пункта при дефиците в запасах (условие 8) следует записать
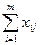 ≤B
≤B 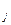 j=1,
j=1, 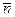 . (10)
. (10)
Таким образом, математическая формулировка транспортной задачи открытого типа (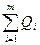 ≠
≠ 
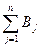 ) имеет вид:
) имеет вид:
Найти минимум функции цели
Z= 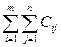 X
X  =min.
=min.
При следующих ограничениях
для случая для случая
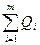 >
> 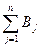
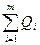 <
< 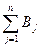
1) х 
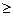 0; 1) х
0; 1) х 
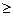 0;
0;
2) 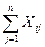 ≤ Q
≤ Q 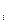 ; 2)
; 2) 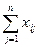 =Q
=Q 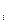 ;
;
3) 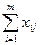 = B
= B 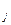 . 3)
. 3) 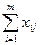 ≤B
≤B 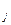 .
.
Открытую модель транспортной задачи при недостатке запасов можно свести к закрытой модели. Для этого необходимо ввести еще один фиктивный пункт отправления (m+1)-й, для которого положим

Q 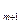 =
= 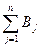 -
- 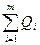 . (11)
. (11)
Стоимость (расстояние) перевозки от фиктивного пункта отправления до каждого пункта потребления положим равной нулю.
В случае превышения запасов над потреблением введем фиктивного потребителя (n+1) мощностью
B 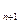 =
= 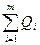 -
- 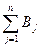 . (11а)
. (11а)
Стоимость перевозок по фиктивным маршрутам также положим равной нулю.
В результате приходим к закрытой модели транспортной задачи, в которой количество груза в пунктах отправления равно количеству груза в пунктах назначения.
При решении транспортных задач встретиться ряд дополнительных ограничений.
ПЕРВОЕ ДОПОЛНИТЕЛЬНОЕ ОГРАНИЧЕНИЕ- отсутствие транспортной связи между каким-либо поставщиком и потребителем. То есть x  =0.В данном случае оценка переменной искусственно завышается на большую величину, так что направление груза по этому маршруту будет невыгодным, так как функция цели всегда стремится к минимуму.
=0.В данном случае оценка переменной искусственно завышается на большую величину, так что направление груза по этому маршруту будет невыгодным, так как функция цели всегда стремится к минимуму.
ВТОРОЕ ДОПОЛНИТЕЛЬНОЕ ОГРАНИЧЕНИЕ- наличие частной заранее фиксированной связи между поставщиками и потребителями, то есть x  =q, искомый объем перевозок от i-го поставщика к j-му потребителю должен быть строго равен величине q. В этом случае до начала решения задачи от соответствующего маршрута вычитается величина q, затем оценка данного маршрута искусственно завышается и задача решается обычным порядком.
=q, искомый объем перевозок от i-го поставщика к j-му потребителю должен быть строго равен величине q. В этом случае до начала решения задачи от соответствующего маршрута вычитается величина q, затем оценка данного маршрута искусственно завышается и задача решается обычным порядком.
ТРЕТЬЕ ДОПОЛНИТЕЛЬНОЕ ОГРАНИЧЕНИЕ заключается в том, что x  ≥q, то есть искомый объем перевозок от i-го поставщика к j-му потребителю должен быть не меньше величины q.В этом случае до начала решения от соответствующего поставщика и потребителя вычитают величину q, затем задачу решают обычным путем.
≥q, то есть искомый объем перевозок от i-го поставщика к j-му потребителю должен быть не меньше величины q.В этом случае до начала решения от соответствующего поставщика и потребителя вычитают величину q, затем задачу решают обычным путем.
3.Методы решения транспортной задачи
Имеется множество методов решения транспортной задачи, из которых наиболее простым являются метод минимального элемента (минимальной стоимости) и потенциалов.
Для решения транспортной задачи составим опорный или начальный план При этом опорным или начальным планом задачи будет такой, для которого все базисные (m+n-1) переменные будут больше нуля. А свободные равны нулю. Методику решения транспортной задачи рассмотрим на конкретном примере.
ПРИМЕР. Имеется три поля: 1,2,3, валовый сбор картофеля на которых соответственно 100,130 и 170 тонн. В хозяйстве имеется также четыре картофелехранилища в которые нужно доставить картофель. Расстояние от каждого поля до каждого хранилища, а также их емкость представлена в таблице 2.
Таблица 2.
Исходные данные по условию задачи
| №№ полей | Валовый сбор картофеля т. | Расстояние от полей до картофелехранилищ, км | |||
х 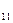
|
 х х 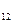
|
х 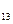
|
х 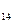
| ||
х 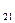
|
х 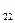
|
х 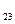
|
х 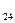
| ||
х 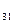
|
х 
|
х 
|
х 
| ||
| Емкость картофелехранилищ, т |
Необходимо составить оптимальный план перевозок с полей в картофелехранилища (однотипными транспортными средствами),обеспечив
минимум грузоперемещений при выполнении всего объема транспортных работ.
Для составления первоначального (опорного) плана используем метод минимального элемента, который предусматривает рассмотрение всех C  таблицы 2 и выбор наименьших из них. Грузы будут перевозиться по тем маршрутам, где расстояние (стоимость) перевозки, т.е. величина C
таблицы 2 и выбор наименьших из них. Грузы будут перевозиться по тем маршрутам, где расстояние (стоимость) перевозки, т.е. величина C  будет минимальной.
будет минимальной.
Заполнение таблицы 2 начинаем с маршрута 2,1,где С  равна 1 и является минимальной.
равна 1 и является минимальной.
Так как валовый сбор с поля 2 меньше,чем потребности хранилища 1, то картофель с поля 2 полностью вывозится в хранилище 1.Хранилище 1 еще может вместить 150-180=20 тонн, которые могут быть доставлены с поля 1, так как после С 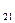 следующим по величине является элемент С
следующим по величине является элемент С 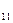 равный 3.Учитывая, что с поля 2 картофель полностью вывезен и хранилище 1 заполнено, выбираем следующий минимальный элемент. Он находится на маршруте 1,2 и равен 5. В хранилище 2 с поля 1 может быть доставлено 100-20=80 тонн картофеля. Следующим минимальным по величине в незаполненных строках и столбцах является элемент маршрута 3,4 равный 7. Хранилище 4 может быть полностью заполнено с поля 3.
равный 3.Учитывая, что с поля 2 картофель полностью вывезен и хранилище 1 заполнено, выбираем следующий минимальный элемент. Он находится на маршруте 1,2 и равен 5. В хранилище 2 с поля 1 может быть доставлено 100-20=80 тонн картофеля. Следующим минимальным по величине в незаполненных строках и столбцах является элемент маршрута 3,4 равный 7. Хранилище 4 может быть полностью заполнено с поля 3.
Следующий минимальный элемент находится на маршруте 3,2 и равен 8. В хранилище 2 с поля 3 может быть завезено 120-80=40 тонн. Оставшийся картофель с поля 8 в количестве 170-50-40=80 тонн может быть полностью помещен в хранилище 3.
Таблица 3
Первоначальный план перевозок
| № хранилища №№ полей | Валовый сбор картофеля, т | ||||
| Емкость картофелехранилища, т | 400=400 |
Суммарная величина грузоперемещений по этому плану составит
Z=3,20+5,80+1,130+8,40+12,80+7,50=2220 ткм.
Улучшить решение задачи, полученное методом минимального элемента, можно, применив для этого метод потенциалов. Введем новые переменные ְα и β.
Переменные α будут соответствовать строкам, а β- столбцам таблицы.
Оптимальное решение транспортной задачи будет достигнуто при следующих условиях:
β 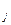 - α
- α 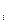 = C
= C  (для всех х
(для всех х  > 0 базисных клеток) (12)
> 0 базисных клеток) (12)
β 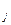 - α
- α 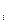 ≤ C
≤ C  (i=1,
(i=1, 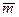 ; j=1,
; j=1, 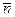 для свободных клеток) (13)
для свободных клеток) (13)
Для транспортной задачи условия (12, 13) называются условиями потенциальности, а ְα и β потенциалами. Если эти условия выполняются, то решение задачи будет оптимальным.
Для нашей задачи ранг матрицы (r =m+n-1) равен r=4+3-1=6(заполнено 6 клеток). Составим для них уравнения вида (12).
Таблица 4
Первая итерация
| № хранилища №№ полей | Валовый сбор картофеля, т | Потенциалы строк | ||||
   1 1
| 5 _ | + | α  =0 =0
| |||
α  =2 =2
| ||||||
 3 3
| 8 + | 12 _ | α 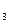 =3 =3
| |||
| Емкость картофелехранилища, т | 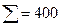
| |||||
| Потенциалы столбцов | β  =3 =3
| β  =5 =5
| β 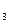 =9 =9
| β 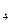 =4 =4
|
β  - α
- α  =3 β
=3 β  - α
- α  =1 β
=1 β 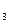 - α
- α 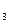 =12
=12
β  - α
- α  =5
=5  β
β  - α
- α 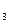 =8 β
=8 β 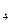 - α
- α 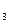 = 7
= 7
Так как число неизвестных превышает на единицу число уравнений, то одну из неизвестных полагаем равной произвольному числу, например α  =0. Потенциалы остальных строк и столбцов найдем из уравнений (12).
=0. Потенциалы остальных строк и столбцов найдем из уравнений (12).
Составим ограничения вида (13) для свободных маршрутов таблицы 3 и проверим решение задачи на оптимальность:
1) β  - α
- α 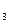 ≤ 7; 2) β
≤ 7; 2) β 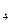 - α
- α  ≤ 11; 3) β
≤ 11; 3) β  - α
- α  ≤ 4;
≤ 4;
4) β 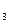 - α
- α  ≤6; 5) β
≤6; 5) β 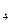 - α
- α  ≤ 3; 6) β
≤ 3; 6) β  - α
- α 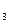 ≤ 5;
≤ 5;
1) 9 < 7; 2) 4 < 11; 3) 3 < 4; 4) 7 < 8;
5) 2 < 3; 6) 6=6.
Наибольшее расхождение наблюдается в первом ограничении, т.е. для маршрута (1,3). Следовательно, условие потенциальности нарушено и полученный план перевозок не оптимален.
Изменим этот план с помощью цикла следующим образом. Назовем циклом в таблице перевозок ломаную линию, которая удовлетворяет таким условиям: каждый отрезок этой линии соединяет лишь два маршрута отдельной строки или столбца и при этом линия будет замкнутой.
Базисные маршруты всегда образуют разомкнутую цепь и, чтобы образовать цикл, нужно присоединить свободный маршрут. Вершины цепи отмечают поочередно знаками «+» и «-», начиная со знака «+» и маршрута, в котором нарушено условие потенциальности.
Среди маршрутов, отмеченных знаком «-» выбираем минимальное количество груза Q=x  . Прибавляем его к маршрутам, отмеченным знаком «+», вычитаем из маршрутов, отмеченных знаком «-».
. Прибавляем его к маршрутам, отмеченным знаком «+», вычитаем из маршрутов, отмеченных знаком «-».
В нашем примере отмечаем маршрут 1-3 знаком «+». (Нарушено условие потенциальности). Соединим его с базисным маршрутом 3-3 и отметим его знаком «-». Замкнем цепь, соединив между собой маршруты 3-2 и 1-2, отметив их соответствующим образом.
В нашем отрицательном полуцикле выберем элемент Q=min {80=80}=80. Этот элемент прибавим и вычтем от соответствующих маршрутов и получим новый план решения задачи (таблица 5).
Таблица 5
Вторая итерация
| №№ храни лищ №№ полей | Валовый сбор картофеля, т | ||||||
α  =0 =0
| |||||||
α  =2 =2
| |||||||
α 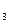 =5 =5
| |||||||
| Емкость картофелехранилища, т | 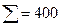
| ||||||
β  =3 =3
| β  =3 =3
| β 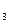 = 7 = 7
| β 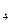 = 2 = 2
|
Учитывая, что число базисных маршрутов при этом получилось меньше, чем ранг матрицы, то при этом один из свободных маршрутов считаем занятым, например, 3-3, количество груза, перевозимого по этому маршруту, принимаем равным нулю.
Полученный план перевозок проверяем на потенциальность по ранее изложенному алгоритму.
Составим ограничения (12) для базовых маршрутов:
1) β  - α
- α  =3; 2) β
=3; 2) β 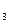 - α
- α  =7; 3) β
=7; 3) β  - α
- α  =1;
=1;
4) β  - α
- α 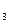 =8 5) β
=8 5) β 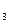 - α
- α 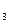 = 12; 6) β
= 12; 6) β 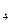 - α
- α 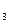 =7.
=7.
α  =0; β
=0; β  =3; β
=3; β 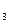 =7; α
=7; α  =2; α
=2; α 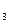 =-5; β
=-5; β  =3; β
=3; β 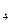 = 2.
= 2.
Проверим условие (13) для свободных маршрутов
1) β  - α
- α  ≤ 5; 2) β
≤ 5; 2) β 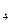 - α
- α  ≤ 11; 3) β
≤ 11; 3) β  - α
- α  ≤ 4;
≤ 4;
4) β 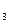 - α
- α  ≤ 8; 5) β
≤ 8; 5) β 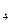 - α
- α  ≤ 3; 6) β
≤ 3; 6) β  - α
- α 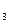 ≤ 8.
≤ 8.
1) 3-0 < 5 2) 2-0 < 7 3) 3-2 <4 4) 7-2 < 8
5) 2-2 < 3 6) 3+5=8.
Условие потенциальности не нарушается, следовательно, нами достигнуто оптимальное решение при величине грузоперемещений
z= 20 х 3+80 х 7+130 х 1+120 х 8+50 х 7=2060 ткм.
Изучение результатов решения задачи позволит использовать потенциалы конечной матрицы не только для проверки оптимальности плана, но и для экономического анализа тех последствий, которые могут возникнуть при изменении первоначальных условий. С помощью потенциалов рассчитывают коэффициенты (оценки) для свободных маршрутов, которые позволяют принимать правильные решения в хозяйственной деятельности. Если в хозяйстве в процессе производства несколько изменились первоначальные условия перевозки или появились дополнительные требования к перевозкам, то можно, не решая задачу заново, скорректировать ее и получить новый оптимальный вариант. Для этого необходимо учесть, что оценка свободного маршрута, в оптимальном плане, означает на сколько ухудшится целевая функция задачи при условии перевозки единицы груза по исследуемому маршруту. Например, для маршрута 1-2 (табл.5) оценка равна (β  - α
- α  -С
-С 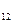 =
= 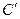
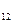 , 3-0-5=-2). Она показывает, что каждая тонна картофеля, завезенная с поля 1 в хранилище2, увеличит грузооборот в хозяйстве на 2 ткм.
, 3-0-5=-2). Она показывает, что каждая тонна картофеля, завезенная с поля 1 в хранилище2, увеличит грузооборот в хозяйстве на 2 ткм.
Если в оптимальном решении в одном или нескольких свободных маршрутах получены нулевые оценки, то это свидетельствует о том, что задача имеет альтернативные решения с равнозначным значением целевой функции.
Варианты и условия выполнения заданий представлены в таблице 1
4.Указания по организации выполнения задания
1.Внимательно прочитать теоретические основы методических указаний.
2.Просуммировать количество груза у поставщика и у потребителя, сравнить полученные суммы. При проведении расчетов учесть, что транспортировка осуществляется однотипными транспортными средствами.
3. В соответствии с методическим указанием открытую модель транспортной задачи свести к закрытой, вводя фиктивный столбец или строку.
4.По приведенному алгоритму, по методу минимального элемента, составить опорный план для решения задачи.
5. Для опорного плана выполнить расчеты по формулам (12) и (13). В наибольшей степени нарушено условие потенциальности в той клетке, где имеет место наибольшая численная величина нарушения условия (13).
6. Решить задачу до конца методом потенциалов. Об окончании решения задачи (получен оптимальный вариант) свидетельствует соблюдение условий потенциальности, проверенных по формулам (12) и (13).
Оптимальную величину грузоперемещений рассчитать по формуле (5) для последней итерации.
Результаты расчетов систематизировать.
Сделать выводы по каждому пункту расчетов.
При выполнении задания на компьютере (исследовательская работа студента) следует получить закономерности изменения определяемых параметров в зависимости от действующих факторов с последующим анализом результатов исследований под руководством преподавателя.
Выполнил ___________________________ Ф.И.О. студента
Принял _____________________________ Ф.И.О. преподавателя