Исследование восприятия человеком цвета показывает, что оно зависит отобстановки и определяется коэффициентами отражения основных цветов. Среднеарифметическим для светлого оттенка будет число 0,59, а для темного– 0,17. Тогда среднеарифметическим между темным и светлым оттенками будет  . Все это подтверждает взаимосвязь «золотого» числа свосприятием цветовых оттенков и целесообразность соблюдения в R5 закона ГПс базовым числом Ф=1,618…. Для удобства проведения исследований ограничимся значением
. Все это подтверждает взаимосвязь «золотого» числа свосприятием цветовых оттенков и целесообразность соблюдения в R5 закона ГПс базовым числом Ф=1,618…. Для удобства проведения исследований ограничимся значением  , которое больше числа 10 и близко к нему. Тогда, с учетом обязательного включения «1» в каждую из прогрессий, R5 преобразуется в R6, R10 в R11 и т.д. Следовательно, R6 будет следующим:
, которое больше числа 10 и близко к нему. Тогда, с учетом обязательного включения «1» в каждую из прогрессий, R5 преобразуется в R6, R10 в R11 и т.д. Следовательно, R6 будет следующим: 
Таблица 14
| Цвет | Оттенок | |
| Светлый | темный | |
| желтый | 0,7 | 0,3 |
| бежевый | 0,65 | 0,25 |
| коричневый | 0,5 | 0,08 |
| красный | 0,35 | 0,1 |
| зеленый | 0,6 | 0,12 |
| синий | 0,5 | 0,05 |
| голубой | 0,55 | 0,25 |
| белый | 0,85 | 0,00 |
| серый | 0,6 | 0,2 |
Сформируем ряд R11, поглощающий в себя
R11: 1,0; 
Если продолжить использовать дальше предложенный выше порядок формирования «золотых» ГП, то получим их большое многообразие, а нам надо выбрать базовое множество, учитывающее значения отклонений размеров (2-3%) не замечаемые глазом.
Исследования показали, что этому требованию на границе 3 % больше всего удовлетворяет знаменатель «золотой» ГП  так как на каждом шаге ГП R91 приращение будет соответствовать примерно 2,7 % и не превышает требуемых 3 %.
так как на каждом шаге ГП R91 приращение будет соответствовать примерно 2,7 % и не превышает требуемых 3 %.  знаменатель ГП (R181)
знаменатель ГП (R181) 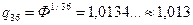 приближается к 1,3 % > 1 % и тем самым может отражать предельно возможную максимальную чувствительность глаза человека. Ведь не случайно на основе
приближается к 1,3 % > 1 % и тем самым может отражать предельно возможную максимальную чувствительность глаза человека. Ведь не случайно на основе  формируется знаменатель для ГП инвариантов ритмов мозга
формируется знаменатель для ГП инвариантов ритмов мозга  Взяв 1,0 за основу ряда, а 1,027094 в качестве базового числа (знаменателя) для формирования «золотой» ГП, получим ряд R91 с граничным значением
Взяв 1,0 за основу ряда, а 1,027094 в качестве базового числа (знаменателя) для формирования «золотой» ГП, получим ряд R91 с граничным значением  Анализ полученного ряда R91 показал, что отношения между соседними числами в нем более равномерны, чем в R80, где перепад достигает 3,6 %>3 %. Если повысить точность с двух знаков до трех знаков после запятой, то отношение между соседними числами для R91 станет равномернее примерно в два раза. Но так как членами рядов из действующей СПЧ являются округленные члены ГП с относительной разностью между расчетными и округленными числами в пределах от +1,26% до -1,01%, то в новой СПЧ эти требования должны также выполняться.
Анализ полученного ряда R91 показал, что отношения между соседними числами в нем более равномерны, чем в R80, где перепад достигает 3,6 %>3 %. Если повысить точность с двух знаков до трех знаков после запятой, то отношение между соседними числами для R91 станет равномернее примерно в два раза. Но так как членами рядов из действующей СПЧ являются округленные члены ГП с относительной разностью между расчетными и округленными числами в пределах от +1,26% до -1,01%, то в новой СПЧ эти требования должны также выполняться.
Сравнительный анализ рядов R80 с R91, имеющих два знака после запятой, показал следующее:
а) в R80 в сравнении с R91 периодически накапливаются погрешности отклонения от постоянного значения отношения двух смежных членов ряда (от знаменателя ГП), которые корректируются в виде четырех колебательных процессов;
б) закономерность накопления погрешности отклонения от постоянного значения отношения двух смежных членов ряда (от знаменателя ГП) в R91 происходит очень медленно при возведении  даже в 90-ю степень, что дает возможность при необходимости расширить границы СПЧ по мере дальнейшего увеличения степени;
даже в 90-ю степень, что дает возможность при необходимости расширить границы СПЧ по мере дальнейшего увеличения степени;
в) в R91 в сравнении с R80 округленные члены ГП с относительной разностью между расчетными и округленными числами находятся не только в пределах от +1,26% до -1,01%,но даже имеют значительный запас этой относительной разности, который в худшем случае достигает примерно 40% относительно верхней границы предельного значения (1,26%).
На основе базового R91 формируются другие ряды, которые могут быть записаны в виде следующих аналитических выражений:
для R46

для R31

для R16

для R11

для R6

Таким образом, полученная 7-рядная (7-уровневая) иерархия для СПЧ, обладает свойствами взаимной вложенности, и может быть использована для уточнения стандартов в различных областях проектирования искусственных объектов на основе перспективных технологий.
Применение СПЧ позволит использовать проявление закономерностей «золотых» ГП для образования параметрических рядов изделий проектируемого объекта, унифицировать и экономически рационально увязывать их между собой с целью выполнения основных требований к реализации технико-экономических характеристик.
Другими словами, с помощью СПЧ могут автономно регулироваться и выбираться, без дополнительных согласований между разработчиками составных частей сложной технической системы, массогабаритные параметры изготовляемой продукции и сооружаемых объектов, мощность, грузоподъемность и т.д.
Немаловажная роль отводится СПЧ в области эргономики.
В настоящее время существуют результаты исследований по стандартизации в авиа- и ракетостроении, космической промышленности, которую предлагается осуществлять с использованием «золотого» числа, взяв за основу шведский стандарт «Гастро-норм». Система «Гастро-норм» одобрена Британским институтом стандартов и будучи универсальной, устанавливает размеры оборудования, функциональных емкостей, контейнеров и стеллажей. Считается, что в основу международных рядов предпочтительных чисел R5, R10, R20, R40, R80, R160 и модульных размеров системы «Гастро-норм» положено значение «золотого» числа, и его «производные».
Однако механизмы реализации «золотого» числа в действующей СПЧ и системе «Гастро-норм» не раскрываются, так как исследования ведутся на уровне анализа и без конкретных предложений по совершенствованию стандартов на основе новой теоретической базы.
Следовательно, теоретически обоснованная новая «золотая» СПЧ может быть в некоторой степени ответом на решение проблем, поднятых в работе. Заложенный принцип формирования базового ряда П80 в СПП дает погрешность до 5% для отдельных пропорций в сравнении с соответствующими им числами из R80, что ставит под сомнение целесообразность их практического использования в высокоточных технологиях.
Если обратить внимание в работе на модульные размеры системы «Гастро-норм», где в качестве пропорций берутся отношения трехзначных чисел, то можно заметить, что благодаря этому повышается точность приближения к числам действующей СПЧ. Однако отношения чисел в системе «Гастро-норм» значительно отличаются от «золотого» числа, так как «золотая» системность в подборе чисел строго не соблюдается.
Наиболее приемлемой для образования СПП из бесконечного множества «золотых» последовательностей может быть последовательность Фибоначчи. Это связано с ее обладанием наибольшей плотностью (количеством) чисел на фиксированном интервале в сравнении с другими последовательностями типа Фибоначчи-Люка.
Выберем трехзначное число «987» из последовательности Фибоначчи, имеющее максимальное значение в рамках тысячи, которое примем за числитель во всех дробных отношениях последовательности П91, образуемой из чисел R91. Узловыми точками П91 будут пропорции, образуемые с помощью знаменателей из чисел последовательности Фибоначчи меньших или равных числу «987» и ограниченных включительно числом, дающим граничную пропорцию
 в ряду R91, то есть когда:
в ряду R91, то есть когда:
987/987=1,0; 987/610  ; 987/377
; 987/377  ; 987/233
; 987/233  ; 987/144
; 987/144  и 987/89
и 987/89  , где все числа в дробях из последовательности Фибоначчи (89, 144, 233, 377, 610, 987). Остальные числа специально подобраны для получения наилучших приближений к СПЧ, а результаты их распределения в знаменателях дробей для П91 приведены в табл. 15
, где все числа в дробях из последовательности Фибоначчи (89, 144, 233, 377, 610, 987). Остальные числа специально подобраны для получения наилучших приближений к СПЧ, а результаты их распределения в знаменателях дробей для П91 приведены в табл. 15
Таблица 15

Из табл. 15 видно, что для точности в 2 знака после запятой погрешность на интервале 1,0 ÷  практически отсутствует, на интервале
практически отсутствует, на интервале  ÷
÷  имеют место редкие отклонения, не более 0,25%, а на интервале
имеют место редкие отклонения, не более 0,25%, а на интервале  ÷
÷  5 – до 0,65%, что равноценно в худшем случае достижению примерно 100% сокращения запаса разности между расчетными и округленными числами, относительно верхней границы предельного значения (1,26%). Такие погрешности незначительны, однако в случае необходимости их уменьшения или полного исключения необходимо выбрать в качестве базового числа (числителя) другое число из последовательности Фибоначчи (большее чем «987») и проделать по отношению к нему ту же процедуру.
5 – до 0,65%, что равноценно в худшем случае достижению примерно 100% сокращения запаса разности между расчетными и округленными числами, относительно верхней границы предельного значения (1,26%). Такие погрешности незначительны, однако в случае необходимости их уменьшения или полного исключения необходимо выбрать в качестве базового числа (числителя) другое число из последовательности Фибоначчи (большее чем «987») и проделать по отношению к нему ту же процедуру.
Общая структурная схема взаимосвязей пользователей с СПЧ и СПП, а также связи между двумя этими системами, приведены на рис. 1. Порядок пользования этими системами в основном не отличается от прежнего, за исключением, предлагается дополнительно ввести возможность учета процедуры выбора масштаба.
Предлагаемые СПЧ и СПП начинают отсчет численных значений с 1,0 в направлении их роста, т.е. производится своего рода «расширение» области чисел в пространственном представлении. Однако опыт исследований (проектирования) дает множество примеров, когда необходимо учитывать обратные соотношения и их обратный рост, т.е. «сжатие» пространства от единицы к нулю.
При формировании обратных значений для чисел из новой СПЧ, то есть для обратного базового ряда R91, целесообразно использовать выражение

В качестве примера покажем образовавшейся обратный ряд R11:
0,1; 









из которого можно выделить R6:
0,1; 




Аналогичным образом формируются обратные ряды: R16, R31, R46, R91 и R181.
Формирование обратной СПП становится еще проще. Для этого в колонке «П91» необходимо поменять в дробях местами числитель со знаменателем и произвести расчеты с округлением до 2-го знака после запятой. В результате образуется обратный базовый ряд П91, из которого известным способом можно получить шесть рядов: П 46, П31, П19, П16, П11 и П6.
Так, например, для П6 получаем: 987/987=1,0; 610/987≈0,62≈Ф; 377/987  ; 233/987
; 233/987  ; 144/987
; 144/987  ; 89/987
; 89/987  ,где числа в числителях и знаменателях из последовательности Фибоначчи.
,где числа в числителях и знаменателях из последовательности Фибоначчи.

Рисунок 1
Таким образом, СПЧ и СПП (рис.1) могут быть расширены обратными системами, что делает их более совершенными для применения.
Заключение
Стандартизация является организационно-правовой и нормативно-технической основой управления качеством продукции. Качество продукции является самым точным и обобщающим показателем научно-технического прогресса, культуры и дисциплины труда.
Объектом теории стандартизации является как сами конкретно существующие и возможные однородные множества повторяющихся объектов, так и их прямые или опосредованные сопряжения, т.е. элементы совместимости реальных предметов, процессов, совокупность которых составляет сложную систему – народное хозяйство.
Теоретической базой развития стандартизации является система предпочтительных чисел. Применение предпочтительных чисел позволяет наилучшим образом осуществлять согласование параметров и размеров отдельно взятого изделия со всеми связанными с ними видами продукции.
В условиях научно-технического прогресса резко возрастает роль стандартизации, как важнейшего звена в системе управления техническим уровнем и качеством продукции на всех стадиях жизненного цикла, стандартизация определяет основу не только настоящего, но и будущего развития хозяйственно-экономической деятельности в стране.
Библиографический список
1. А.И.Аристов и др., Метрология, стандартизация и сертификация / А.И. Аристов, Л.И.Карпов, В.П. Приходько, Т.М.Раковщик.-М.: Издательский цент «Академия», 2006 -384с.
2. Р.А Егошин, Справочник стандартизатора, Издательство «Прапор», 2000г.
3. С.Н.Гаврилов, Ряды предпочтительных чисел – Москва, Издательство стандартов – 1999г.
4. ГОСТ 8032-84 «Предпочтительные числа и ряды предпочтительных чисел»
5. ГОСТ 6636-69 «Основные нормы взаимозаменяемости. Нормальные линейные размеры»