КОНТРОЛЬНАЯ РАБОТА
По дисциплине
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫИ ПРИКЛАДНЫЕ МОДЕЛИ
Вариант №2
Брянск - 2009
ЗАДАЧА 1
Решить графическим методом типовую задачу оптимизации
Совхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не менее 6 единиц питательного вещества А и не менее 12 единиц питательного вещества В. Какое количество корма надо расходовать ежедневно на одного животного, чтобы затраты были минимальными? Использовать данные таблицы:
| Корма Питат. вещества | Количество питательных веществ в 1 кг корма | |
| А В | ||
| Цена 1 кг корма, т.руб. | 0,2 | 0,3 |
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум и почему?
Решение. Данная задача оптимизации является задачей линейного программирования. Обозначим виды кормов через х 1 и х 2. Целевой функцией задачи является общая стоимость кормов, затраченных на кормление животных, которая должна быть наименьшей. Число ограничений задачи равно числу питательных веществ, входящих в состав кормов - 2. Дополнительно вводится условие неотрицательности переменных. Зная цены кормов, содержание питательных веществ в них можно сформулировать математическую модель задачи линейного программирования:
Строим область допустимых решений задачи (см. рис.1).
Область допустимых решений задачи
Строим вектор-градиент целевой функции задачи. За его начало принимаем точку с координатами, равными коэффициентам целевой функции по соответствующим координатным осям 0,2 (1; 1,5), тогда концом вектора-градиента будет являться точка с координатами (0; 0). Перпендикулярно вектору-градиенту строится прямая, которая характеризует поведение целевой функции:
Для определения положения точки минимума целевой функции прямая, перпендикулярная вектору-градиенту, смещается в его направлении до тех пор, пока она не покинет область допустимых решений. Предельная точка области допустимых решений при этом движении и является точкой минимума.
В нашей задаче - это точка В, образованная пересечением граничных прямых ограничений I и II. Ее координаты определяются решением системы
уравнений этих прямых:
откуда x 1*=2; x 2*=2 и 
.
Таким образом, чтобы достичь минимальных затрат, следует расходовать ежедневно на одного животного по 2 кг каждого вида корма при затратах в 1 тыс. руб.
Решение данной задачи линейного программирования на максимум лишено экономического смысла, так как затраты на корм стремятся уменьшить. Однако математически эта задача имеет решение и на максимум: наибольшее значение в области допустимых решений целевая функция принимает в точке (0; 6), и это значение равно
.
|
рис. 1 - Графическое решение задачи линейного программирования
ЗАДАЧА 2
Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования
Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
| А | Б | В | Г | ||
| I II III | |||||
| Цена изделия |
Требуется:
1) Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
2) Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
3) Пояснить нулевые значения переменных в оптимальном плане.
4) На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья II и III вида на 120 и 160 единиц соответственно и уменьшении на 60 единиц запасов сырья I вида;
- оценить целесообразность включения в план изделия "Д" ценой 12 ед., на изготовление которого расходуется по две единицы каждого вида сырья.
Решение. 1. Данная задача оптимизации является задачей линейного программирования.
Обозначим количество выпускаемых изделий х1, х2, х3, х4.
Целевой функцией задачи является общая стоимость выпускаемой продукции, которая должна быть наибольшей. Число ограничений задачи равно числу ресурсов, используемых для изготовления изделий - 3.
Дополнительно вводится условие неотрицательности переменных.
Зная цены изделий, нормы их расхода и запасы ресурсов, формулируем математическую модель исходной задачи линейного программирования:
Задачу оптимизации решаем с помощью надстройки «Поиск решения » табличного процессора EXCEL (меню «Сервис »):
|
рис. 2 - Надстройка «Поиск решения»
Использование надстройки позволило получить значения переменных оптимального плана выпуска изделий: Х *=(95; 210; 0; 0). Целевая функция имеет наибольшее для данных условий задачи значение f (X *)=2115 (прил. 1).
Таким образом, для получения наибольшей выручки от реализации продукции следует производить x 1*=95 изделий А, x 2*=210 изделий Б и не производить изделия В (x 3*=0) и Г (х4 *=0).
2. Обозначим двойственные оценки ресурсов I, II, III как y 1, y 2, y 3 соответственно. Целевой функцией двойственной задачи является общая стоимость запасов ресурсов в двойственных оценках, которая должна быть наименьшей. Число ограничений двойственной задачи равно числу переменных исходной задачи - 4. Математическая модель двойственной задачи имеет вид:
При решении исходной задачи с помощью EXCEL одновременно определяется и оптимальное решение двойственной задачи. В «Отчете по устойчивости » (прил. 2) приводятся теневые цены ресурсов: y 1*=0; y 2*=1,5; y 3*=2,25.
Наименьшее значение целевой функции двойственной задачи
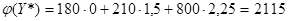
совпадает с наибольшим значением целевой функции исходной задачи f (X *). Следовательно, оптимальный план двойственной задачи определен верно.
3. Выпуск изделий В и Г невыгоден для данных условий задачи. Это объясняется тем, что затраты по ним превышают цену на 0,5 и 5 соответственно:
Таким образом, выпуск изделий В и Г убыточен и поэтому эти изделия не вошли в оптимальный план (x 3*=0) и (х4 *=0).
4. Проанализируем использование ресурсов в оптимальном плане. Для этого подставим в ограничения исходной задачи значения переменных оптимального плана Х *=(95; 210; 0; 0) и проверим выполнение неравенств:
Видно, что ресурсы II и III используются в оптимальном плане полностью и являются дефицитными, т.е. сдерживающими рост целевой функции. Они имеют отличные от нуля оценки y2* =1,5 и y3* =2,25.
Увеличение объема ресурса II на одну единицу при неизменных объемах других ресурсов ведет к росту наибольшей выручки на 1,5 руб., а увеличение объема ресурса III на единицу - на 2,25 руб.
Ресурс I имеет нулевую двойственную оценку (y1 *=0) и является недефицитными, т. е. избыточным в оптимальном плане. Увеличение объемов этого ресурса не повлияет на оптимальный план выпуска продукции и не увеличит ее общую стоимость.
Определим, насколько изменится выручка выпускаемой продукции при заданных изменениях запасов сырья. Из «Отчета по устойчивости » видно, что эти изменения происходят в пределах устойчивости (см. «Допустимое увеличение »и«Допустимое уменьшение » правых частей ограничений в прил. 2), что дает возможность сразу рассчитать изменение наибольшей выручки от реализации выпускаемой продукции, не решая новую задачу линейного программирования:
При этом «новая» наибольшая выручка составит:
руб.
Изменение запасов ресурсов привело не только к изменению значения целевой функции на 540 тыс. руб., но и к изменению плана выпуска. При этом структура плана не изменилась: изделия, которые были убыточны, не вошли и в новый план выпуска, т.к. цены на сырье не изменялись. Новый план выпуска составляет 75 единиц изделий А и 330 ед. изделий Б.
Для определения целесообразности включения в план выпуска еще и изделия Д с заданными характеристиками, рассчитаем стоимость ресурсов на изготовление единицы этого изделия в теневых ценах и сравним это значение с ценой реализации:
Следовательно, продукцию Д выпускать выгодно, так как затраты на нее меньше, чем ее стоимость.
ЗАДАЧА 3