В течение девяти последовательных недель фиксировался спрос Y(t) (млн. р.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен ниже в таблице:
| t | yt |
Требуется:
1) Проверить наличие аномальных наблюдений.
2) Построить линейную модель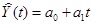 
, параметры которой оценить МНК (
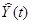- расчетные, смоделированные значения временного ряда).
3) Построить адаптивную модель Брауна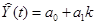 
с параметром сглаживания a= 0,4 и a= 0,7; выбрать лучшее значение параметра сглаживания α.
4) Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7-3,7).
5) Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
6) По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%).
7) Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Вычисления провести с одним знаком в дробной части. Основные промежуточные результаты вычислений представить в таблицах (при использовании компьютера представить соответствующие листинги с комментариями).
Решение. 1. Для выявления аномальных наблюдений используем метод Ирвина. Для каждого уровня временного ряда рассчитывается статистика
,
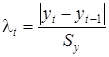где 
- стандартное отклонение уровней ряда.
Стандартное отклонение определяется с помощью встроенной функции EXCEL «СТАНДОТКЛОН»: Sy =7,29 млн. руб. Расчет значений t для всех уровней ряда, начиная со второго. Табличное значение критерия Ирвина для уровня значимости a=0,05 и длины временного ряда n =9 составляет l=1,5. Видно, что ни одно из значений l t не превышает критического значения, что свидетельствует об отсутствии аномальных наблюдений.
|
|
2. Линейную трендовую модель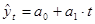 
строим с помощью надстройки EXCEL «Анализ данных… Регрессия »:
Уравнение линейного тренда имеет вид (см. «Коэффициенты »):
.
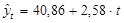Угловой коэффициент показывает, что спрос на кредитные ресурсы финансовой компании за одну неделю возрастает в среднем на 2,58 млн. руб.
Коэффициент детерминации уравнения R 2»0,941 превышает критическое значение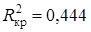 
для a=0,05 и n =9, что свидетельствует о статистической значимости линейной модели и наличии устойчивого линейного тренда во временном ряду. Само значение R 2 показывает, что изменение спроса во времени на 94,1 % описывается линейной моделью.
3. Построение адаптивной модели Брауна. Модель Брауна строится в несколько этапов.
1) По первым пяти точкам временного ряда методом наименьших квадратов оцениваем параметры а 0 и а 1 линейной модели
.
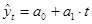Получаем начальные значения параметров модели Брауна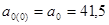 
и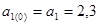 
, которые соответствуют моменту времени t =0 (определены с помощью функций EXCEL «ОТРЕЗОК » и «НАКЛОН » соответственно.
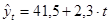
2) Находим прогноз на первый шаг (t =1):
.
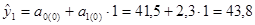3) Определяем величину отклонения расчетного значения от фактического:
.
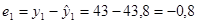4) Скорректируем параметры модели для параметра сглаживания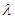 
=0,4 по формулам:
|
|
;
,
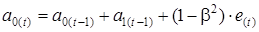где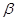 
- коэффициент дисконтирования данных, отражающий степень доверия к более поздним наблюдениям; 
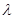- параметр сглаживания ( = 
); 
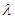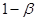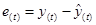- отклонение (остаточная компонента).
По условию 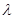=0,4, следовательно значение b равно:
.
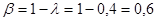Получим:
;
,
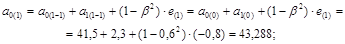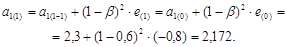5) По модели со скорректированными параметрами a 0( t ) и a 1( t ) находим прогноз на следующий момент времени:
.
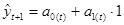Для t =2:
.
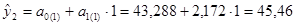6) Возвращаемся к пункту 3 и повторяем вычисления до конца временного ряда.
7) Вычислим среднюю относительную ошибку для данного параметра сглаживания:
8) Корректировка параметров модели для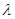 
=0,7 и 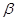=0,3:
;
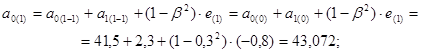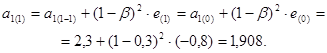
9) Средняя относительная ошибка для данного параметра:
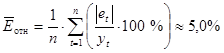
Таким образом, судя по средней относительной ошибке при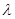 
=0,4 и 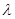=0,7, в первом случае 
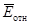=4,1%, а во втором случае 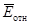=5,0%. Следовательно, 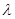=0,4 – лучшее значение параметра сглаживания, т.к. средняя относительная ошибка меньше.
4. Оценим адекватность линейной модели. Рассчитанные по модели значения спроса 
, остатки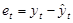 
и их график были получены вEXCEL одновременно с построением модели (см. «ВЫВОД ОСТАТКА » в прил. 4).
Случайность остаточной компоненты проверим по критерию поворотных точек. В нашем случае общее число поворотных точек в ряду остатков составляет p =4.
Критическое число поворотных точек для a=0,05 и n =9 определяется по формуле
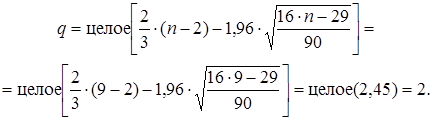
Так как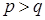 
, остатки признаются случайными.
Проверим независимость остатков с помощью критерияДарбина–Уотсона (отсутствие автокорреляции).Для расчета d ‑статистики используется выражение, составленное из встроенных функций EXCEL:
d ‑статистика имеет значение (см. прил. 4):
;
|
|
;
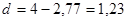Критические значения d ‑статистики для a=0,05 и n =9 составляют: d 1=0,82; d 2=1,32. Так как выполняется условие
,
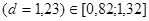то нет достаточных оснований сделать тот или иной вывод о выполнении свойства независимости. Проверим независимость остатков по коэффициенту автокорреляции первого порядка, который равен (см. прил. 4):
.
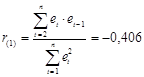Для расчета коэффициента автокорреляции использовалось выражение, составленное из встроенных функций EXCEL:
Критическое значение коэффициента автокорреляции для a=0,05 и n =9 составляет 0,666. Так как коэффициент автокорреляции не превышает по абсолютной величине критическое значение, то это указывает на отсутствие автокорреляции в ряде динамики. Следовательно, модель по этому критерию адекватна.
Проверим равенство нулю математического ожидания уровней ряда остатков. Среднее значение остатков равно нулю: 
(определено с помощью встроенной функции «СРЗНАЧ »; см. прил. 4). Поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
Нормальный закон распределения остатков проверяем с помощью R / S -критерия, определяемого по формуле
,
где e max; e min - наибольший и наименьший остатки соответственно (определялись с помощью встроенных функций «МАКС » и «МИН »);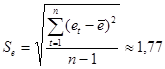 
- стандартное отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН »; см. прил. 4).
Критические границы R/S -критерия для a=0,05 и n =9 имеют значения: (R / S)1=2,7 и (R / S)2=3,7. Так как R / S -критерий попадает в интервал между критическими границами, то ряд остатков признается соответствующим нормальному закону распределения вероятностей. Модель по этому критерию адекватна.
Таким образом, выполняются все пункты проверки адекватности модели: модель признается адекватной исследуемому процессу.
Оценим адекватность построенной модели Брауна: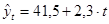 
с параметром сглаживания 
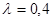(см. таблица 2):
Таблица 2 - Анализ ряда остатков модели Брауна
| Проверяемое свойство | Используемые статистики | Граница | Вывод | ||
| наименование | значение | нижняя | верхняя | ||
| Независимость | d –критерий Дарбина-Уотсона r(1) -коэффициент автокорреляции | d =2,79
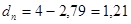-0,44
| 0,82 | 1,32 0,666 | Нельзя сделать вывод по этому критерию r(1) <0,666 адекватна |
| Случайность | Критерий пиков (поворотных точек) | 6>2 | адекватна | ||
| Нормальность | RS-критерий | R/S=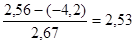 
| 2,7 | 3,7 | неадекватна |
| Мат.ожидание≈0 | t-статистика Стьюдента |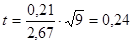  
| 2,306 | адекватна | |
| Вывод: модель статистически неадекватна |
5. Оценим точность линейной модели на основе использования средней относительной ошибки аппроксимации.
Среднюю относительную ошибку аппроксимации находим по формуле:
%
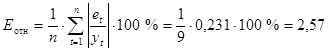Значение E отн показывает, что предсказанные моделью значения спроса на кредитные ресурсы отличаются от фактических значений в среднем на 2,57 %. Модель имеет хорошую точность.
Оценим точность модели Брауна с параметром сглаживания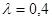 
:
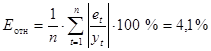
Модель Брауна также имеет хорошую точность, однако она несколько ниже, чем у линейной трендовой модели.
6. Строим точечный и интервальный прогнозы спроса на 1 и 2 недели вперед для линейной модели:
Прогноз на 1 неделю вперед (период упреждения k =1):
1) Точечный прогноз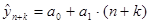 
:
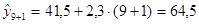млн. руб.
Среднее прогнозируемое значение спроса равно 64,5 млн. руб.
2) Интервальный прогноз
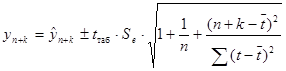
с надежностью (доверительной вероятностью) g=0,7. необходимые расчеты приведены в таблице 3:
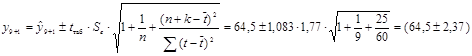млн. руб.,
где t таб=1,083 - табличное значение t -критерия Стьюдента для доверительной вероятности g=0,7.
С вероятностью 70 % фактическое значение спроса на кредитные ресурсы будет находиться в интервале от 62,13 до 66,87 млн. руб.
Таблица 3
| t | yt | 
| ||
| Среднее | - | |||
Прогноз на 2 недели вперед (период упреждения k =2):
1) Точечный прогноз:
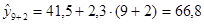млн. руб.
Среднее прогнозируемое значение спроса равно 66,8 млн. руб.
2) Интервальный прогноз с надежностью g=0,7:
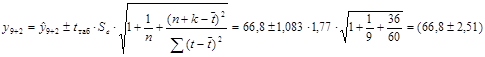млн. руб.,
С вероятностью 70 % фактическое значение спроса на кредитные ресурсы будет находиться в интервале от 64,29 до 69,31 млн. руб.
Построим прогноз для модели Брауна на следующие 2 недели. Параметры модели, полученные для последнего уровня временного ряда (т. е. для t = n =9), используются для построения прогноза спроса по формуле:
.
Прогноз на 1 неделю вперед (период упреждения k =1):
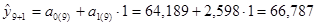млн. руб.
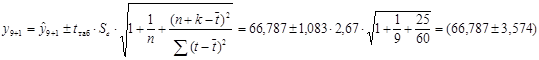
С вероятностью 70 % значение спроса на кредитные ресурсы будет находиться в интервале от 63,213 до 70,361 млн. руб.
Прогноз на 2 недели вперед (период упреждения k =2):
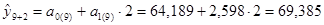млн. руб.
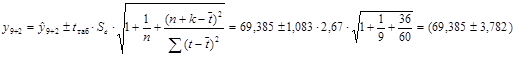
Значение спроса на кредитные ресурсы будет находиться в интервале от 65,603 до 73,167 млн. руб.
7. График временного ряда спроса строим с помощью надстройки «Диаграмма » EXCEL. Предварительно выделяется блок ячеек «t » и «yt » вместе с заголовками, а затем выбирается пункт меню «Вставка» «Диаграмма… »:
Далее строим линию линейного тренда (меню «Диаграмма» ® «Добавить линию тренда… » ® «Линейная »), и устанавливаем «Прогноз » вперед на 2 единицы и назад на 1 единицу, а также вывод на диаграмме уравнения тренда и коэффициента детерминации R 2.