Иррациональным будем называть уравнение, в котором неизвестное содержится под знаком радикала или под знаком возведения в дробную степень. Рассмотрим некоторые способы решения иррациональных уравнений:
I. Решение иррациональных уравнений по определению арифметического корня натуральной степени:
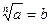
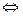
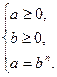
Например:
1) Решите уравнение: 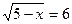 .
.
Решение: 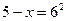 ; ОДЗ:
; ОДЗ: 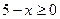 ;
;
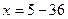 ;
; 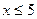 .
.
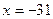 .
.
Ответ: 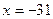 .
.
2) Решите уравнение: 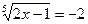 .
.
Решение: 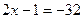 ;
;
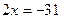 ;
;
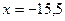 .
.
Ответ: 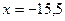 .
.
3) Решите уравнение: 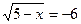 .
.
Решение: т.к. арифметическим корнем четной степени является неотрицательное число, то данное уравнение не имеет решений.
4) Решите уравнение: 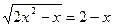 .
.
Решение: 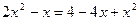 ; ОДЗ:
; ОДЗ: 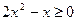 ;
;
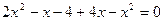 ;
; 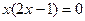 ;
;
 ;
; 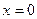 либо
либо 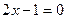 ;
;
по теореме, обратной теореме Виета: 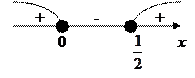
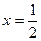 ;
;

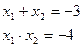
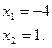
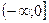 ;
; 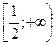
Доп. условие: 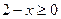 ;
;
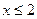 .
.
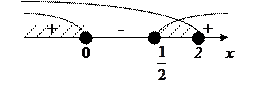
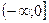 ;
; 
Ответ: 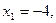
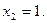
5) Решите уравнение: 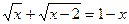 .
.
Решение: ОДЗ: 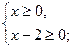
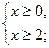
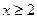 .
.
Доп. условие: 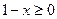 ;
;
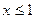 .
.
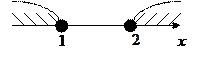
решений нет
Ответ: нет решений.
Решение уравнений:
1) Задания для классной работы (№151(1,3,5,7); №152(1); №153(1); №154(1, 4); №155(1,3), №183(1,3,5)) [1, с.60,68]:
1. 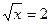 ;
;
2. 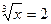 ;
;
3. 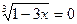 ;
;
4. 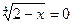 ;
;
5. 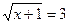 ;
;
6. 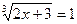 ;
;
7. 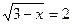 ;
;
8. 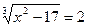 ;
;
9. 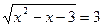 ;
;
10. 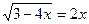 ;
;
11. 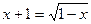 ;
;
12. 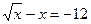 ;
;
13. 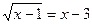 ;
;
14. 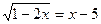 ;
;
15. 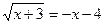
16. 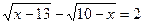 ;
;
17. 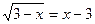 ;
;
18. 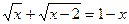 .
.
2) Задания для домашнее работы (№151(2,4,6); №152(2); №153(2); №154(2,); №155(2,4); №183(2,4,6)) [1, с.60,68]:
1. 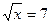 ;
;
2. 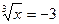 ;
;
3. 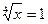 ;
;
4. 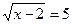 ;
;
5. 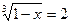 ;
;
6. 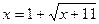 ;
;
7. 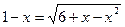 ;
;
8. 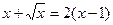 ;
;
9. 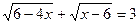 ;
;
10. 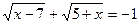 .
.
3) Задания для самостоятельной работы:
Вариант I
Решите уравнение:
1.  ;
;
2. 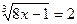 ;
;
3. 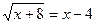 ;
;
4. 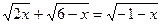 .
.
Вариант II
Решите уравнение:
1. 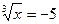 ;
;
2. 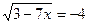 ;
;
3. 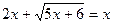 ;
;
4. 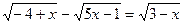 .
.

 II. Использование свойств монотонности функций при решении иррациональных уравнений:
II. Использование свойств монотонности функций при решении иррациональных уравнений:



Утверждение: Если на промежутке 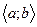 две функции имеют различные монотонности, то графики этих функций на данном промежутке имеют не более одной общей точки.
две функции имеют различные монотонности, то графики этих функций на данном промежутке имеют не более одной общей точки.
Т.о. уравнение 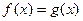 , где
, где 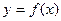 и
и 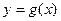 – функции разной монотонности, имеет не более одного корня.
– функции разной монотонности, имеет не более одного корня.
Замечания:
1) Функция 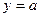 , где a – действительное число, является постоянной.
, где a – действительное число, является постоянной.
2) Функция 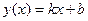 , где
, где 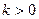 , является возрастающей для любого действительного значения аргумента.
, является возрастающей для любого действительного значения аргумента.
Функция 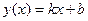 , где
, где 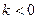 , является убывающей для любого действительного значения аргумента.
, является убывающей для любого действительного значения аргумента.
3) Функция 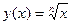 является возрастающей для любого действительного значения аргумента из области определения.
является возрастающей для любого действительного значения аргумента из области определения.
4) Функция 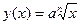 , где
, где 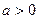 , является возрастающей для любого действительного значения аргумента из области определения.
, является возрастающей для любого действительного значения аргумента из области определения.
Функция 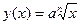 , где
, где 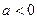 , является убывающей для любого действительного значения аргумента из области определения.
, является убывающей для любого действительного значения аргумента из области определения.
5) Функция 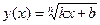 , где
, где 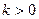 , является возрастающей для любого действительного значения аргумента из области определения.
, является возрастающей для любого действительного значения аргумента из области определения.
Функция 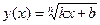 , где
, где 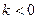 , является убывающей для любого действительного значения аргумента из области определения.
, является убывающей для любого действительного значения аргумента из области определения.
6) Функция 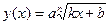 , где
, где 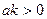 , является возрастающей для любого действительного значения аргумента из области определения.
, является возрастающей для любого действительного значения аргумента из области определения.
Функция 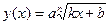 , где
, где 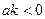 , является убывающей для любого действительного значения аргумента из области определения.
, является убывающей для любого действительного значения аргумента из области определения.
Например:
1) Решите уравнение: 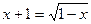 .
.
 Решение:
Решение: 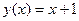 – возрастающая функция значит, уравнение имеет не
– возрастающая функция значит, уравнение имеет не
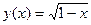 – убывающая функция более одного корня x =0
– убывающая функция более одного корня x =0
Ответ: x =0.
2) Решите уравнение: 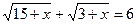 .
.
Решение: 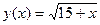 – возрастающая функция
– возрастающая функция
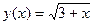 – возрастающая функция
– возрастающая функция

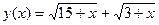 – возрастающая функция значит, уравнение
– возрастающая функция значит, уравнение
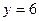 – постоянная функция имеет не более од-
– постоянная функция имеет не более од-
ного корня x =1
Ответ: x =1.
Решение уравнений:
1) Задания для классной работы (№154(1,3); №156(3); 158(1,3); №1157(2))
[1, с.60,61,322]:
1. 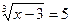 ;
;
2. 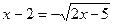 ;
;
3. 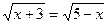 ;
;
4. 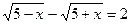 ;
;
5. 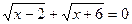 ;
;
6. 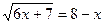 ;
;
7. 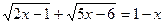 ;
;
8. 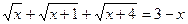 ;
;
9. 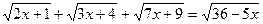 ;
;
10. 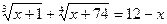 .
.
2) Задания для домашней работы (№158(2,4); №159(1)) [1, с.61]:
1. 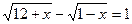 ;
;
2. 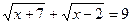 ;
;
3. 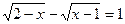 ;
;
4. 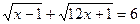 ;
;
5. 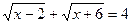 ;
;
6. 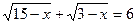 ;
;
7. 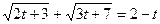 ;
;
8. 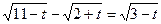 ;
;
9. 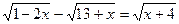 ;
;
10. 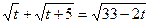 .
.
III. Решение иррациональных уравнений вида 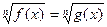 :
:
| Вид уравнения | Решение |
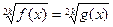 , где k –натуральное число , где k –натуральное число
| 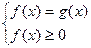 или или 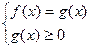
|
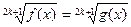 , где k – натуральное число , где k – натуральное число
| 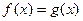
|
Например:
1) Решите уравнение: 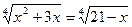 .
.
Решение: 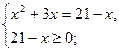
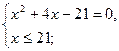
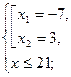
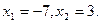
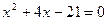 ;
;
 по теореме, обратной теореме Виета:
по теореме, обратной теореме Виета:
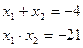
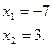
Ответ: 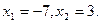
2) Решите уравнение: 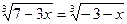 .
.
Решение: 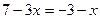 ;
;
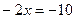 ;
;
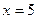 .
.
Ответ: x =5.
3) Решите уравнение: 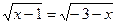 .
.
Решение: 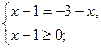
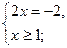
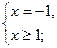 данная система решений не имеет.
данная система решений не имеет.
Ответ: нет решений.
Решение уравнений:
1) Задания для классной работы:
1. 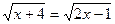 ;
;
2. 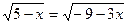 ;
;
3. 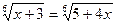 ;
;
4. 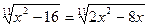 ;
;
5. 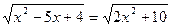 .
.
2) Задания для домашней работы:
1. 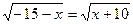 ;
;
2. 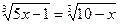 ;
;
3. 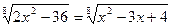 .
.
IV. Решение иррациональных уравнений вида 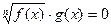 :
:
1. Уравнение 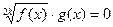 , где k – нат. число, равносильно
, где k – нат. число, равносильно 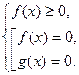
2. Уравнение 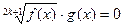 , где k – нат. число, равносильно
, где k – нат. число, равносильно 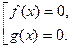

Например:
Решите уравнение: 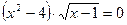 .
.
Решение: 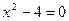 либо
либо 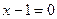 ; ОДЗ:
; ОДЗ: 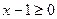 ;
;
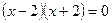
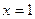 ;
;  .
.

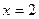 либо
либо 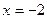
не удовлетворяет ОДЗ.
Ответ: 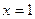 ,
, 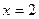 .
.
Решение уравнений:
1) Задания для классной работы:
1. 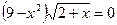 ;
;
2.  .
.
2) Задания для домашней работы:
1. 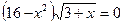 ;
;
2. 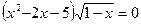 .
.
V. Возведение обеих частей уравнения в одну и ту же степень:
| Вид уравнения | Условия | Решение |
1. 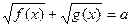
| 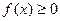 , , 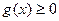 , Д.У.: , Д.У.: 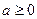
| 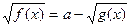 ; ;
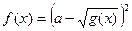
|
2. 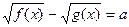
| 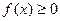 , , 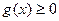
| 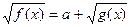 ; ;
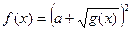
|
3. 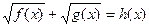
| 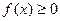 , , 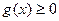 ,
Д.У.: ,
Д.У.: 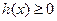
| 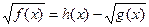 ; ;
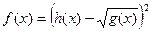
|
4. 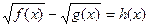
| 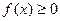 , , 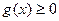
| 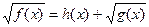 ; ;
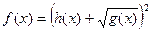
|
5. 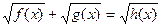
| 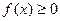 , , 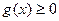 , , 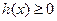
| 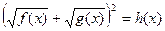
|
6. 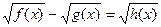
| 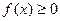 , , 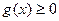 , , 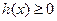
| 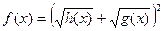
|
7. 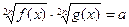
| 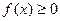 , , 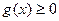 , Д.У.: , Д.У.: 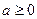
| 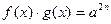
|
8. 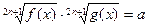
| 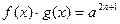
| |
9. 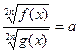
| 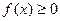 , , 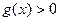 , Д.У.: , Д.У.: 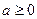
| 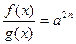
|
10. 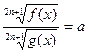
| 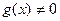
| 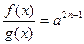
|
При решении иррациональных уравнений, приведенных выше в таблице, необходимо выполнить проверку полученных в результате решения значений неизвестного.
Например:
1) Решите уравнение: 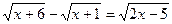 .
.
Решение: возведём обе части уравнения в квадрат
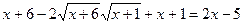 ;
;
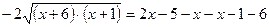 ;
;
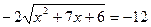 ;
;
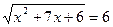 ; возведём обе части полученного уравнения в квадрат
; возведём обе части полученного уравнения в квадрат
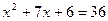 ;
;
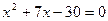 ;
;
по теореме, обратной теореме Виета:

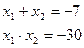
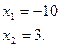
Проверка показывает, что 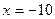 не является корнем исходного уравнения.
не является корнем исходного уравнения.
Ответ: 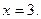
2) Решите уравнение: 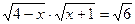 .
.
Решение: возведём обе части уравнения в квадрат
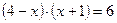 ;
;
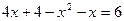 ;
;
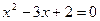 ;
;
по теореме, обратной теореме Виета:

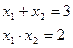
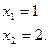
Проверка показывает, что оба значения неизвестного являются корнями данного уравнения.
Ответ: 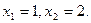
Решение уравнений:
1) Задания для классной работы (№156(1,2); №159(2); №187(1,3)) [1, с.60,69]:
1. 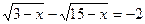 ;
;
2. 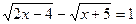 ;
;
3.  ;
;
4. 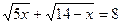 ;
;
5. 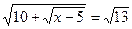 ;
;
6. 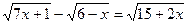 ;
;
7. 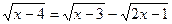 ;
;
8. 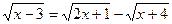 .
.
2) Задания для домашней работы (№156(4); №187(2,4)) [1, с.60,69]:
1. 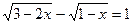 ;
;
2. 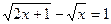 ;
;
3. 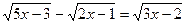 ;
;
4. 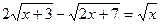 ;
;
5. 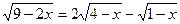 ;
;
6. 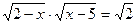 .
.
VI. Введение вспомогательной переменной с целью понижения степени иррационального уравнения:
Решите уравнение: 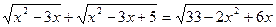 .
.
Решение:
Выполним замену: 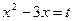 ;
;
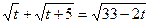 ;
;
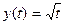 – возрастающая функция;
– возрастающая функция;
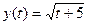 – возрастающая функция;
– возрастающая функция;

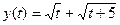 – возрастающая функция значит, уравнение имеет не более
– возрастающая функция значит, уравнение имеет не более
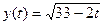 – убывающая функция одного корня t =4
– убывающая функция одного корня t =4
Обратная замена: 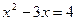 ;
;
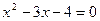 ;
;
 по теореме, обратной теореме Виета:
по теореме, обратной теореме Виета:
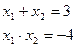
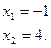
Проверка показывает, что оба значения неизвестного являются корнями данного уравнения.
Ответ: 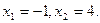
Решение уравнений:
1) Задания для классной работы:
1. 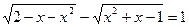 ;
;
2. 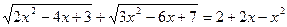 .
.
2) Задания для домашней работы:
1. 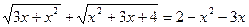 ;
;
2. 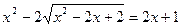 .
.
VII. Введение вспомогательной переменной с целью исключения иррациональности:
Решите уравнение: 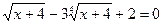 .
.
Решение:
Выполним замену: 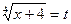 ;
;
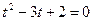 ;
;
по теореме, обратной теореме Виета:

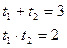
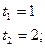
Обратная замена:
1) 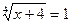 ; 2)
; 2) 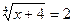 ;
;
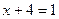 ;
;  ;
;
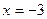 .
. 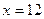 .
.
Проверка показывает, что оба значения неизвестного являются корнями данного уравнения.
Ответ: 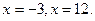
Решение уравнений:
1) Задания для классной работы (№188(1,3,5)) [1, с.69]:
1. 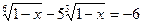 ;
;
2. 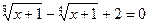 ;
;
3. 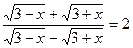 .
.
2) Задания для домашней работы (№188(2,4)) [1, с.69]:
1. 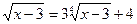 ;
;
2. 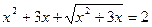 .
.
VIII. Графический способ решения иррациональных уравнений:
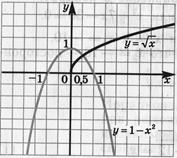
Решите уравнение: 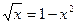 .
.
|
Решите графически уравнения:
1) Задания для классной работы (№162(1,3)) [1, с.61]:
1. 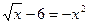 ;
;
2. 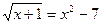 ;
;
3. 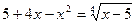 ;
;
4. 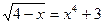 .
.
2) Задания для домашней работы (№162(2,4)): 1. 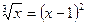 ; 2.
; 2. 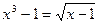 .
.
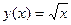 и
и 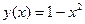 . Графики пересекаются в одной точке при
. Графики пересекаются в одной точке при 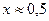 .
Ответ:
.
Ответ: