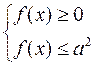I. Недельное домашнее задание: «Решение иррациональных уравнений»
Решите уравнение:
1. 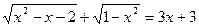 ; 8.
; 8. 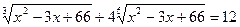 ;
;
2. 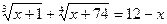 ; 9.
; 9. 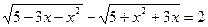 ;
;
3. 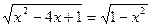 ; 10.
; 10. 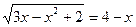 ;
;
4. 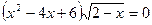 ; 11.
; 11. 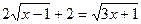 ;
;
5. 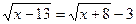 ; 12.
; 12. 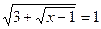 ;
;
6. 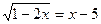 ; 13.
; 13. 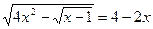 ;
;
7. 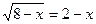 ; 14.
; 14. 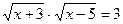 .
.
II. Самостоятельная работа: «Решение иррациональных уравнений »
Вариант I
Решите уравнение:
1. 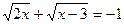 ; 5.
; 5. 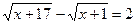 ;
;
2. 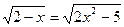 ; 6.
; 6. 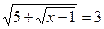 ;
;
3. 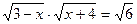 ; 7.
; 7. 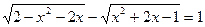 .
.
4. 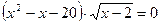 ;
;
Вариант II
Решите уравнение:
1. 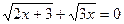 ; 5.
; 5. 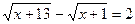 ;
;
2. 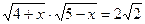 ; 6.
; 6. 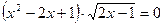 ;
;
3. 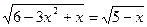 ; 7.
; 7. 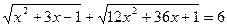 .
.
4. 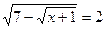 ;
;
III. Обобщающий урок: «Иррациональные уравнения и способы их решения»
Обучающая цель: продолжить формировать умения решать иррациональные уравнения различных видов, применяя все изученные способы их решения, за счет обобщения и систематизации теоретических знаний и практических умений по данной теме.
Задачи урока:
1. Рассмотреть обобщающую таблицу: «Виды иррациональных уравнений и способы их решения » с целью повторить теоретический материал данной темы.
2. Продолжить учить определять вид иррационального уравнения и способы его решения.
Этапы урока:
I. Повторение теоретического материала (7-10 мин)
Для любых 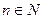 и любых
и любых 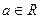
| Вид уравнения | Условия | Решение |
1. 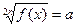
| 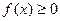 , Д.У.: , Д.У.: 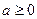
| 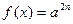
|
2. 
| 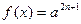
| |
3. 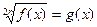
| 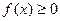 , Д.У.: , Д.У.: 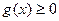
| 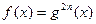
|
4. 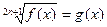
| 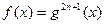
| |
5. 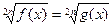
| 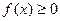 или или 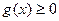
| 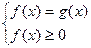 или или 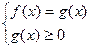
|
6. 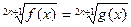
| 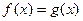
| |
7. 
| 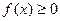
| 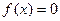 , , 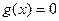
|
8. 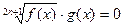
| 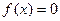 , , 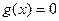
| |
9. 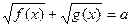
| 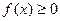 , , 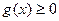 , Д.У.: , Д.У.: 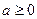
| 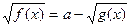 ; ;
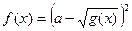
|
10. 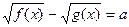
| 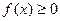 , , 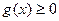
| 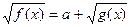 ; ;
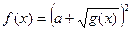
|
11. 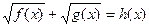
| 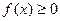 , , 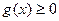 , Д.У.: , Д.У.: 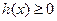
| 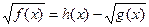 ; ;
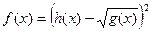
|
12. 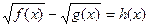
| 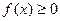 , , 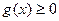
| 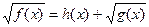 ; ;
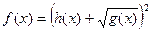
|
13. 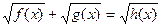
| 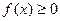 , , 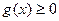 , , 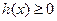
| 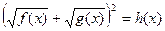
|
14. 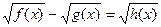
| 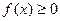 , , 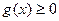 , , 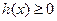
| 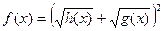
|
15. 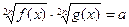
| 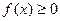 , , 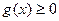 , Д.У.: , Д.У.: 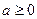
| 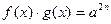
|
16. 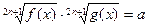
| 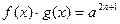
| |
17. 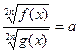
| 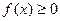 , , 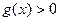 , Д.У.: , Д.У.: 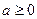
| 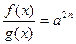
|
18. 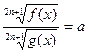
| 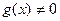
| 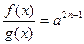
|
Основные способы решения иррациональных уравнений:
1. По определению арифметического корня натуральной степени;
2. Использование свойств монотонности функций;
3. Введение вспомогательной переменной с целью понижения степени иррационального уравнения;
4. Введение вспомогательной переменной с целью исключения иррациональности;
5. Возведение в квадрат;
6. Графический способ.
II. Решение уравнений
| Способ | № | Решение уравнений | Ответ |
| 1. | 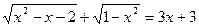
| ||
| 2. | 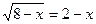
| ||
| 3. | 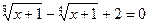
| ||
| 4. | 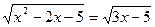
| ||
| 5. | 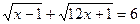
| ||
| 6. | 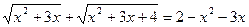
| ||
| 7. | 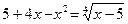
| ||
| 8. | 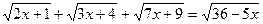
| ||
| 9. | 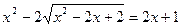
| ||
| 10. | 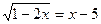
| ||
| 11. | 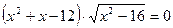
| ||
| 12. | 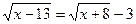
| ||
| 13. | 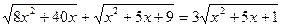
| ||
| 14. | 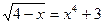
| ||
| 15. | 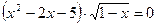
| ||
| 16. | 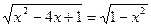
| ||
| 17. | 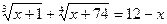
|
III. Домашнее задание: решить все уравнения, которые не успели в классе.
Иррациональные неравенства и способы их решения
 Решение простейших иррациональных неравенств
Решение простейших иррациональных неравенств
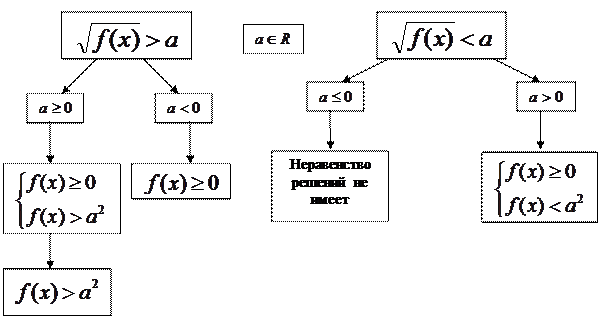

|
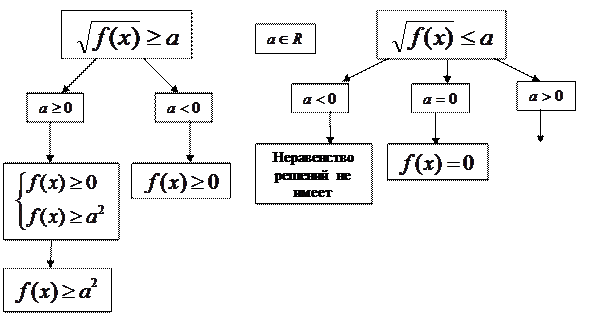
Например:
1) Решите неравенство: 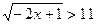 .
.
Решение:  ;
;
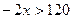 ;
;
 .
.
Ответ:  .
.
2) Решите неравенство: 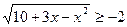 .
.
Решение: 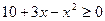 ;
;
решим квадратное уравнение 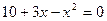 ;
;
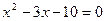 ;
;
 по теореме, обратной теореме Виета:
по теореме, обратной теореме Виета:

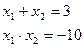
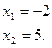
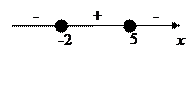
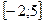
Ответ: 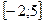 .
.
3) Решите неравенство: 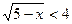 .
.
Решение: 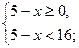
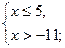
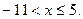
Ответ: 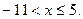
4) Решите неравенство: 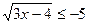 .
.
Решение: т.к. арифметическим корнем четной степени является неотрицательное число, то данное неравенство решений не имеет.
Ответ: неравенство решений не имеет.
5) Решите неравенство: 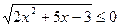 .
.
Решение:  ;
;
 ;
;
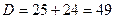 ;
;
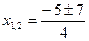 ;
;
 ;
; 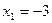 .
.
Ответ:  ;
; 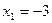 .
.
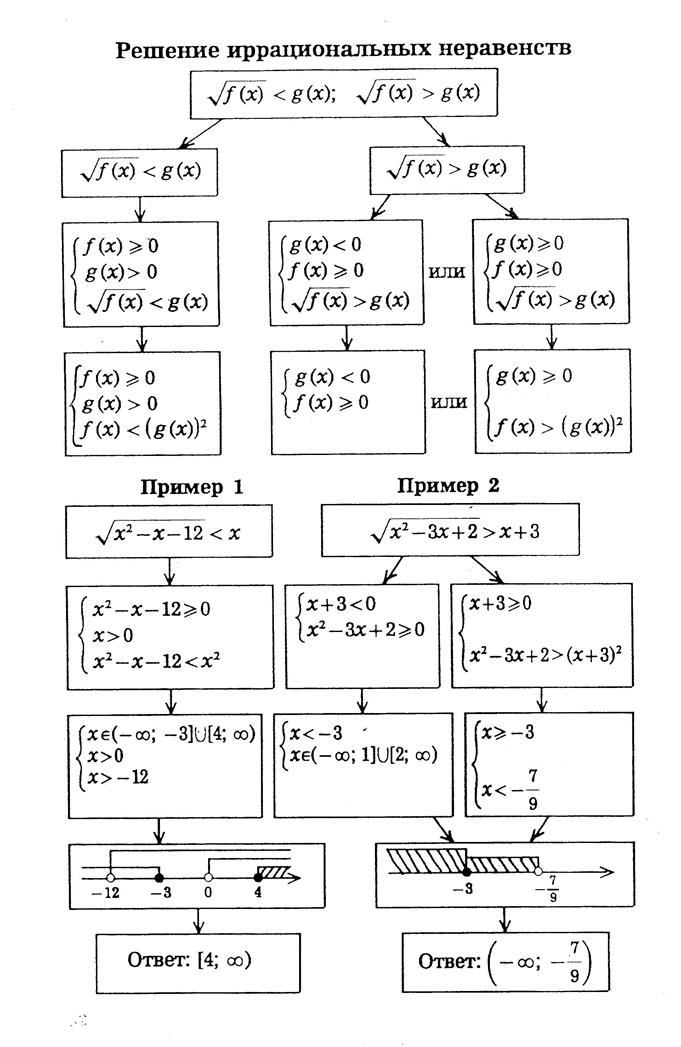
Решение неравенств:
1) Задания для классной работы:
1. №166-№169(нечетн.) [1, с.66];
2. № 172-173(нечётн.) [1, с.67];
3. 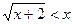 ;
;
4. 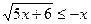 ;
;
5. 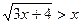 ;
;
6. 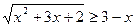 ;
;
7. 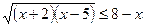 ;
;
8. 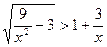 .
.
2) Задания для домашней работы:
1. №166-№169(четн.) [1, с.66];
2. № 172-173(чётн.) [1, с.67];
3. 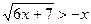 ;
;
4. 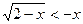 ;
;
5. 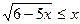 ;
;
6. 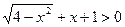 ;
;
7. 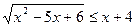 .
.
Контрольная работа: «Иррациональные уравнения и неравенства »
Вариант I
1. Решите уравнения:
а) 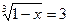 ; д)
; д) 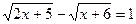 ;
;
б) 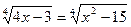 ; е)
; е) 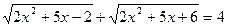 ;
;
в) 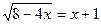 ; ж)
; ж) 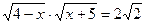 .
.
г)  ;
;
2. Решите неравенства:
а) 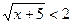 ; в)
; в) 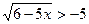 ;
;
б) 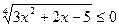 ; г)
; г) 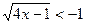 .
.
Вариант II
1. Решите уравнения:
а) 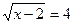 ; д)
; д) 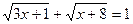 ;
;
б) 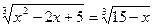 ; е)
; е) 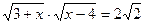 ;
;
в) 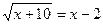 ; ж)
; ж) 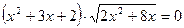 .
.
г) 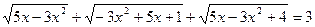 ;
;
2. Решите неравенства:
а) 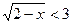 ; в)
; в) 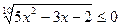 ;
;
б) 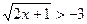 ; г)
; г) 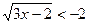 .
.
Литература
1. «Алгебра и начала анализа 10-11» Ш.А. Алимов и др. – 11-е изд. – М.: Просвещение, 2003. – 384 с.
2. «Дидактические материалы по алгебре и началам анализа для 10 класса общеобразовательных учреждений» М.И. Шабунин и др. – М.: Просвещение, 2006. – 189 с.
3. «Иррациональные уравнения и неравенства» А.Х. Шахмейстер – 2 изд. – СПб.: ЧеРо-на-Неве, 2004. – 192 с.