Контрольная работа №3 (раздел III, тема 3. 1, 3. 2))

ВАРИАНТ 1

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

3. Записать данную выборку в виде таблицы частот, найти эмпирическую функцию распределения и построить её график.

4. среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию, исправленное среднее квадратическое отклонение

5,7	9,0	17,6	11,65	0,5	18,25	16,8	10,3	1,4	6,65
14,0	4,2	11,1	20,0	12,7	2,55	13,5	14,1	6,15	16,5
4,6	13,9	15,0	3,8	19,6	9,4	15,9	19,5	17,8	3,1
12,2	0,3	16,45	18,0	5,35	17,7	18,8	2,9	11,55	12,25
11,4	2,4	12,8	7,3	13,7	12,5	0,9	10,25	14,8	8,8
7,8	18,0	1,75	8,0	11,5	5,1	15,3	8,4	13,2	10,7

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,999 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=2, объём выборки n=9 и выборочное среднее =44,6.

ЗАДАЧА 3

Утверждается, что результат действия лекарства зависит от способа его применения А, В, С. Проверить это утверждение при α=0,05 по следующим данным таблицы.

Результат	А	В	С
Неблагоприятный
Благоприятный

ЗАДАЧА 4

По заданной корреляционной таблице, X(млн. руб.) производственные средства Y(т) суточная выработка определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	14-19	19-24	24-29	29-34	34-39
16-18
18-20
20-22
22-24
24-26

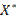=22

ВАРИАНТ 2

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

8,25	12,3	7,15	17,9	9,4	3,15	7,5	4,5	11,85	14,8
6,0	4,2	10,7	0,3	13,2	6,25	8,6	14,5	2,9	5,0
11,8	8,1	10,0	8,0	3,8	5,4	10,1	9,9	13,1	8,9
9,55	18,0	5,6	9,25	11,35	15,6	10,8	6,8	3,75	11,9
12,7	7,4	13,6	7,25	7,2	0,9	12,75	16,3	7,0	7,75
2,85	14,0	1,0	6,9	11,95	8,8	9,8	7,8	15,1	9,65

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,95 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=9, объём выборки n=16 и выборочное среднее .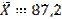

ЗАДАЧА 3

Комплектующие изделия одного наименования поступают с трёх предприятий A,B,C.Результаты проверки изделий следующие

Результаты проверки	А	В	С	Всего
Годные
Негодные
Всего

Можно ли считать, что качество изделий не зависит от поставщика? Принять α=0,10

ЗАДАЧА 4

По заданной корреляционной таблице, где X возраст и Y дневная выработка молодых рабочих определить

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	14-19	19-24	24-29	29-34	34-39
16.5-18.5
18.5-20.5
20.5-22.5
22.5-24.5
24.5-26.5
26.5-28.5

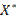=20

ВАРИАНТ 3

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

5,7	9,0	17,6	11,65	0,5	18,25	16,8	10,3	1,4	6,65
14,0	4,2	11,1	20,0	12,7	2,55	13,5	14,1	6,15	16,5
4,6	13,9	15,0	3,8	19,6	9,4	15,9	19,5	17,8	3,1
12,2	0,3	16,45	18,0	5,35	17,7	18,8	2,9	11,55	12,25
11,4	2,4	12,8	7,3	13,7	12,5	0,9	10,25	14,8	8,8
7,8	18,0	1,75	8,0	11,5	5,1	15,3	8,4	13,2	10,7

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,99 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=3, объём выборки n=16 и выборочное среднее .

ЗАДАЧА 3

Во время эпидемии гриппа изучалась эффективность прививок против этого заболевания. Получены следующие данные

	После прививки	Без прививки
Заболели
Не заболели

Указывают ли эти результаты на эффективность прививок? Принять α=0,01

ЗАДАЧА 4

По заданной корреляционной таблице, где X возраст и Y дневная выработка молодых рабочих определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	20-25	25-30	30-35	35-40	40-45	45-50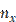
16-18
18-20
20-22
22-24
24-26

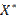=23

ВАРИАНТ 4

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

12,5	17,8	9,0	7,30	1,75	18,0	14,1	11,55	8,8	5,7
4,2	18,25	1,4	11,5	14,8	19,6	5,35	19,5	2,55	16,5
9,4	7,8	17,7	18,0	12,8	3,1	14,0	18,8	15,0	12,2
17,6	20,0	4,6	13,7	11,4	11,65	10,7	16,45	16,8	13,5
13,9	12,25	15,3	2,4	8,0	0,3	12,7	6,15	13,2	6,65
0,9	15,9	10,25	3,8	5,1	11,1	8,4	0,5	10,3	2,9

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,999 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=4, объём выборки n=9 и выборочное среднее .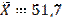

ЗАДАЧА 3

При измерении производительности двух агрегатов получены следующие результаты

№замера
Агрегат А	14,1	10,1	14,7	13,7	14,0
Агрегат В	14,0	14,5	13,7	12,7	14,1

Можно ли считать, что производительности агрегатов А и В одинаковы, в предположении, что обе выборки получены из нормально распределённых генеральных совокупностей. Принять α=0,10

ЗАДАЧА 4

По заданной корреляционной таблице, где X возраст и Y дневная выработка молодых рабочих определить:

3. Коэффициент корреляции;

4. Уравнение регрессии Y на X и X на Y.

Y X	15-20	20-25	25-30	30-35	35-40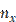
16-18
18-20
20-22
22-24
24-26
26-28

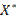=24

ВАРИАНТ 5

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

16,1	7,5	11,0	18,8	6,95	4,7	2,2	9,5	22,5	11,8
4,3	14,0	1,0	7,4	17,2	11,2	15,6	24,0	23,0	2,9
19,9	10,8	12,8	18,0	13,5	21,4	0,7	8,6	5,8	9,75
8,95	20,8	8,9	4,5	12,2	8,0	20,9	11,5	15,0	13,25
12,9	1,45	16,7	0,3	10,15	14,3	4,9	17,35	9,3	6,2
5,6	19,6	5,15	10,65	8,8	3,8	13,0	6,7	1,5	10,1

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,95 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=8, объём выборки n=16 и выборочное среднее =28,4.

ЗАДАЧА 3

Количество бракованных деталей в партии не должно превышать 5%. В результате контроля 100 деталей из этой партии обнаружено 8 бракованных. Можно ли считать, что процент брака превосходит допустимый при α=0,01?

ЗАДАЧА 4

По заданной корреляционной таблице, где X возраст и Y дневная выработка молодых рабочих определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	14-18	18-22	22-26	26-30	30-34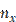
17-19
19-21
21-23
23-25
25-27
27-29

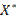=25

ВАРИАНТ 6

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

2,55	2,7	3,9	5,25	1,0	6,5	4,1	10,1	3,6	1,9
1,6	5,8	0,75	11,6	4,35	2,25	5,85	2,0	4,15	5,5
5,55	8,7	8,8	4,3	9,6	10,5	2,9	5,3	6,6	7,8
4,7	12,0	4,8	2,5	5,45	0,3	6,25	1,15	5,95	3,8
5,9	3,35	9,3	7,0	1,4	5,1	7,9	9,9	5,4	4,25
0,8	2,4	1,55	2,8	2,6	3,85	3,15	6,3	0,35	8,25

ЗАДАЧА 2

ЗАДАЧА 3

Из суточной продукции цеха случайным образом отобрано и проверено 200 приборов. При этом 16 приборов признаны негодными к эксплуатации. Можно ли считать, что негодная продукция цеха составляет 90%, если α=0,10?

ЗАДАЧА 4

По заданной корреляционной таблице,X(млн. руб.) производственные средства Y(т) суточная выработка определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	10-14	14-18	18-22	22-26	26-30	30-34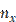
15-25
25-35
35-45
45-55
55-65

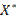=17

ВАРИАНТ 7

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

9,1	12,0	7,8	14,1	4,2	1,0	8,5	6,1	14,8	17,85
7,9	3,1	9,5	7,55	6,0	10,3	18,0	10,9	2,8	1,4
13,8	8,25	0,65	9,6	10,1	6,6	0,4	4,4	8,6	11,0
3,5	9,3	3,25	8,35	2,5	12,75	14,65	16,9	17,5	14,9
12,3	5,8	12,6	0,5	11,2	5,35	10,8	1,2	16,45	8,7
0,7	15,0	5,4	11,6	4,9	13,4	7,4	15,75	5,1	16,2

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,999 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=6, объём выборки n=9 и выборочное среднее =68,9.

ЗАДАЧА 3

Ниже приведены результаты выборочной проверки мужчин и женщин

	Мужчины	Женщины
Дальтоники
Не дальтоники

Проверить, есть ли зависимость между дальтонизмом и полом человека, при α=0,05.

ЗАДАЧА 4

По заданной корреляционной таблице, X(млн. руб.) производственные средства Y(т) суточная выработка определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	8-14	14-20	20-26	26-32	32-28	38-44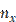
10-20
20-30
30-40
40-50
50-60

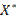=19

ВАРИАНТ 8

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

1,8	10,7	6,5	4,3	3,6	2,0	0,55	11,65	5,25	8,5
9,25	12,6	6,0	1,95	9,7	6,15	8,65	13,15	3,95	12,1
13,0	6,9	9,2	10,2	1,4	4,9	9,4	0,7	7,25	14,25
3,4	4,5	0,75	5,95	8,8	5,5	5,4	14,6	14,55	7,6
11,4	1,3	10,8	0,4	5,8	4,25	2,3	8,1	12,35	14,7
4,8	10,9	3,0	8,9	2,8	7,2	11,9	5,3	15,0	4,1

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,95 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=2, объём выборки n=9 и выборочное среднее =29,7.

ЗАДАЧА 3

В результате длительных наблюдений установлено, что вероятность полного выздоровления больного, принимавшего лекарство А, равна 0,8. Новое лекарство В назначено 800 больным, причём 660 из них полностью выздоровели. Можно ли считать новое лекарство значимо эффективнее лекарстваА при уровне значимости α=0,15.

ЗАДАЧА 4

По заданной корреляционной таблице, X(млн. руб.) производственные средства Y(т) суточная выработка определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	10-20	20-30	30-40	40-50	50-60	60-70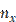
10-18
18-26
26-34
34-42
42-50
50-58

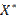=25

ВАРИАНТ 9

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

10,1	4,6	18,0	3,15	9,5	14,0	0,4	5,1	11,45	7,6
1,3	12,8	16,2	17,8	8,85	15,9	9,0	13,5	20,0	2,6
15,1	7,9	9,6	4,0	3,5	17,3	13,15	18,35	5,2	16,7
8,0	17,9	12,5	7,8	14,8	12,9	4,7	2,0	19,4	14,4
4,25	8,3	0,6	11,75	10,5	1,1	11,3	7,0	3,6	5,65
12,2	0,95	15,0	6,2	6,9	16,25	9,25	7,3	11,7	6,7

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,99 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=7, объём выборки n=16 и выборочное среднее 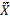=66,3.

ЗАДАЧА 3

Для оценки качества изделий, изготовленных двумя заводами, взяты выборки =200 и =300 изделий. В этих выборках оказалось соответственно 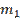=20 и =15 бракованных деталей. При уровне значимости α=0,05 проверить гипотезу о равенстве вероятностей изготовления бракованного изделия обоими заводами

ЗАДАЧА 4

По заданной корреляционной таблице, X(млн. руб.) производственные средства Y(т) суточная выработка определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	10-18	18-26	26-34	34-42	42-50	50-58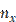
12-20
20-28
28-36
36-44
44-52
52-60

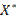=30

ВАРИАНТ 10

Задача 1

1. Записать интервальный статистический ряд распределения частот наблюдаемых значений случайной величины.

2. Построить гистограмму частот случайной величины.

9,15	1,85	8,4	6,35	14,7	3,0	15,0	10,25	14,85	10,8
6,0	6,2	14,15	12,6	16,9	9,7	11,3	6,8	4,1	14,9
11,1	16,3	0,9	9,2	8,2	17,3	14,3	13,0	10,55	11,6
14,0	5,6	16,0	13,2	15,5	12,8	0,4	15,4	17,7	4,65
8,6	15,9	13,6	11,0	2,15	10,9	10,1	3,55	18,0	7,15
1,2	12,2	8,7	5,25	9,4	5,0	11,95	7,8	4,8	13,1

ЗАДАЧА 2

Найти доверительный интервал для оценки с надёжностью γ=0,999 неизвестного математического ожидания a нормально распределённой случайной величины, если известны среднее квадратическое отклонение Ϭ=4, объём выборки n=25 и выборочное среднее =48,2.

ЗАДАЧА 3

Технология производства некоторого вещества дает в среднем 1000 кг в сутки со средним квадратическим отклонением Ϭ=80 кг. Новая технология производства в среднем дает 1100 кг вещества в сутки с тем же Ϭ. Можно ли считать, что новая технология обеспечивает повышение производительности, при α=0,25?

ЗАДАЧА 4

По заданной корреляционной таблице, X(млн. руб.) производственные средства Y(т) суточная выработка определить:

1. Коэффициент корреляции;

2. Уравнение регрессии Y на X и X на Y.

Y X	10-16	16-22	22-28	28-34	34-40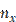
14-20
20-26
26-32
32-38
38-44
44-50

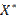=35

Контрольная работа №3 (раздел III, тема 3. 1, 3. 2))

Поиск по сайту